Метод контурных токов

3.4.Выделяют на схеме 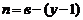независимых контуров (независимый контур должен отличаться от любого другого контура хотя бы на одну новую ветвь), выбирают условные положительные направления, обходя каждый из этих контуров (по или против часовой стрелке часов), и составляют n уравнений в соответствии со II законом Кирхгофа вида:

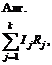
где – число ЭДС в рассматриваемом контуре; – число падений напряжений на резисторах данного контура.

При этом падение напряжений в правой части уравнений и ЭДС в левой части записываются со знаком “+”, если условные положительные направления соответствующих токов и ЭДС совпадают с принятым направлением обхода рассматриваемого независимого контура и со знаком “–” в противоположном случае.

3.5.Тем или иным математическим методом решают совместно полученную систему, содержащую 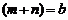линейных уравнений относительно искомых токов в ветвях схемы; при этом топология рассчитываемых схем такова, что число ветвей обычно соответствует числу резисторов в схеме.

3.6.Для токов, получивших в результате решения знак “–”, необходимо на схеме изменить принятые ранее произвольно условные положительные направления на противоположные.

8

В случае использования метода непосредственного применения законов Кирхгофа для сокращения затрат на математические вычисления студент может воспользоваться специальной компьютерной программой кафедры РЭ “Расчет сложной цепи постоянного тока”, позволяющей не только решить систему линейных уравнений -го порядка методом Гаусса (выбор главных элементов по столбцу, приведение путем необходимых линейных преобразований левых частей уравнений к диагональному виду), но и проверить выполнение баланса отдаваемой и потребляемой мощностей в схеме, т. е. убедиться в правильности решения; при этом проверяется выполнение функционала вида:

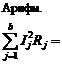
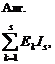
где – число ветвей или резисторов в схеме; – число источников ЭДС.

В правой части приведенного выражения слагаемые записываются со знаком “+”, если условные положительные направления ЭДС и тока в рассматриваемой активной ветви совпадают (источник работает в режиме отдачи электроэнергии во внешнюю цепь) и со знаком “–” в противоположном случае (источник работает как приемник электроэнергии, т. е. его действие подавляется за счет других, более мощных источников и сложившегося распределения сопротивлений ветвей схемы).

В случае использования указанной программы необходимо привести полученную систему линейных уравнений к канонической векторно-матричной форме вида:

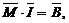
где – квадратная матрица коэффициентов левой части системы линейных уравнений размерности ; – вектор-столбец искомых токов; – вектор-столбец свободных членов.

При этом в случае отсутствия в том или ином уравнении системы слагаемого, соответствующего какому-либо из искомых токов, в необходимой клеточке матрицы ставится коэффициент 0. Таким образом, необходимые исходные данные должны быть представлены в следующей форме:

9

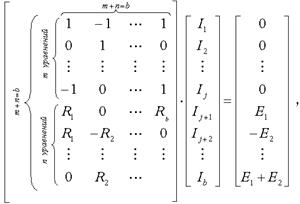
где 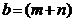– число ветвей или число резисторов в схеме.

4 МЕТОД КОНТУРНЫХ ТОКОВ

Этот метод более экономичен, чем предыдущий, так как позволяет уменьшить число совместно решаемых линейных уравнений, поскольку число уравнений в этом случае соответствует числу независимых контуров в рассматриваемой схеме. Однако он несколько формален и менее нагляден.

При использовании данного метода можно рекомендовать такую последовательность расчета:

4.1.Выбирают число 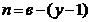независимых контуров, где – число ветвей в схеме, – число узлов.

4.2.Принимают, что в каждом контуре течет свой гипотетический контурный ток, который обозначают на схеме замкнутой по контуру кривой, снабженной стрелкой, соответствующей принятому направлению контурного тока. Это направление во всех контурах принимают одинаковым (по часовой стрелке или против нее). Ток в —м контуре обозначают (, и т. д.) (рис. 4.7).

4.3.Вычисляют полные (или собственные) сопротивления контуров как сумму сопротивлений каждого контура, например:

·  по ІІ закону Кирхгофа (рис. 4.7)

;

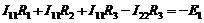10

·  тогда

.

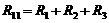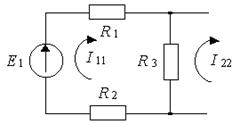
Рисунок 4.7

4.4.Вычисляют взаимные (общие) сопротивления 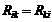смежных контуров как сумму сопротивлений ветви, общей для -го и -го контуров. Если -й и -й контуры не имеют смежных ветвей, то 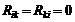. Для рассмотренного примера .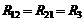