Метод мма для колебательных систем с малыми нелинейностями
(4.15)
Для свободных колебаний системы с нелинейностью (P = 0) из (4.14) получим уравнения
|
|
(4.16) |
Здесь w — основная частота свободных колебаний нелинейной системы, заменившая частоту w1, которая задавалась внешним воздействием. Из последней системы можно найти соотношение между амплитудами гармоник
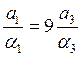 .
.
Нетрудно убедиться, что из системы (4.16) можно получить частоту свободных колебаний:
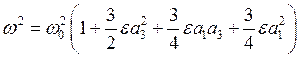 .
.
Как мы видим, w отличается от w0 лишь на величину порядка e.
Иначе обстоит дело при наличии воздействия (P ¹ 0). Тогда частота возбуждаемого колебания будет задаваться внешним воздействием. В рассматриваемом случае частота w0 близка к 3w1. В результате соотношение между амплитудами основного колебания и его третьей гармоники должно быть совсем иным.
Для определения a1 и a3 имеем систему (4.14). Заменяя из (4.16) в первом уравнении a1 на w2a1, получаем
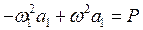 ,
,
откуда выражение для амплитуды основной гармоники
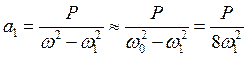 .
.
Здесь мы учли, что w » w0 (с точностью до величины порядка e), а w0 » 3w1.
|
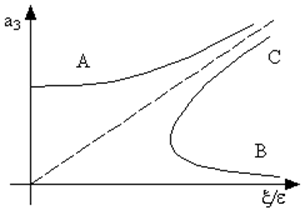
Рис. 31. Амплитуда третьей гармоники. |
Для определения a3 воспользуемся вторым соотношением из (4.14), тогда, подставив его во второе уравнение системы (4.15), получим
Введём относительную расстройку x:
тогда получим уравнение третьей степени относительно a3: |
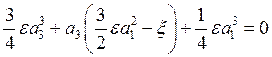 .
.
Так как e ¹ 0, то на e можно сократить
|
|
(4.17) |
Это решение описывает установившийся процесс. Таким образом, нелинейность зависит от отношения x/e. Зависимость амплитуды третьей гармоники от этого отношения представлена на рис. 31.
4.4. Метод ММА для колебательных систем с малыми нелинейностями и потерями при гармоническом силовом воздействии
Общая запись уравнений для неавтономной системы первого порядка при силовом воздействии:
|
|
(4.18) |
В предельном случае если m ® 0, тогда получаем неоднородное ДУ вида
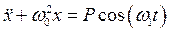 ,
,
решение которого будет x0(t) = acos(w1t), где амплитуда колебаний
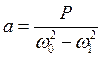 .
.
Возвращаясь к (4.18) и считая нелинейность слабой, будем искать решение в виде
|
|
(4.19) |
Подставляя это решение в исходное уравнение, можно записать
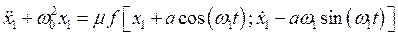 .
.
Видно, что это уравнение вида (3.8). Для возможности применения метода ММА необходимо потребовать, чтобы внешняя сила была мала по амплитуде и имела бы тот же порядок малости, что и малые силы, связанные с нелинейными и диссипативными свойствами системы и возникающие при конечных амплитудах колебаний в ней. В таком случае воздействующую силу можно объединить с этими малыми силами и свести рассмотрение задачи к приближенному исследованию уравнения типа
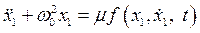 ,
,
которое отличается от рассмотренного ранее (см. (3.8)) тем, что функция f1 зависит не только от переменной x и её производной, но и явно от времени.
Вводя в исходное уравнение новый масштаб времени t = w1t, получим
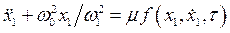 .
.
Вводя обозначение 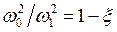 и требуя, чтобы расстройка x была величиной порядка малости m, запишем
и требуя, чтобы расстройка x была величиной порядка малости m, запишем
![]() .
.
В правой части этого уравнения малые параметры; обозначив 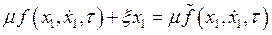 , запишем окончательно
, запишем окончательно
|
|
(4.20) |
Тогда можно решить это уравнение в соответствии с методом ММА.
В качестве простейшего примера рассмотрим вынужденные колебания в контуре с нелинейным затуханием R(i) = R0(1 + g0i2) (см. рис. 26). Для подобного контура мы можем записать уравнение Кирхгофа в виде
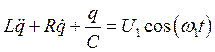 .
.
Если считать, что собственная частота контура w0 близка к частоте внешней силы w1, то, вводя обозначения
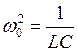 ,
, 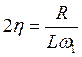 ,
, 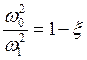 ,
, 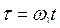 ,
, 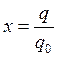 ,
,
приходим к уравнению
|
|
(4.21) |
где
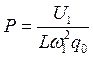 ,
, 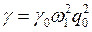 .
.
Для применимости метода ММА к решению этого уравнения необходимо потребовать, чтобы выполнялись неравенства: расстройка x << 1, затухание в системе 2h << 1, амплитуда внешнего воздействия P << 1, т. е. чтобы все члены в правой части уравнения были малы по сравнению с членами в левой его части.
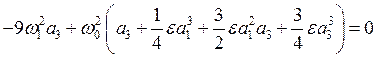 .
.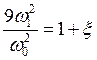 ,
,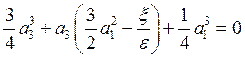 .
.

