Метод векторных диаграмм при анализе дифракции
И первое и второе слагаемые в уравнении (4) равны проекциям на ось ординат векторов с модулями ![]() и
и ![]() , вращающихся с одинаковыми угловыми скоростями w. Их сумма равна проекции на ось ординат суммы векторов. По теореме косинусов, модуль суммы —
, вращающихся с одинаковыми угловыми скоростями w. Их сумма равна проекции на ось ординат суммы векторов. По теореме косинусов, модуль суммы —
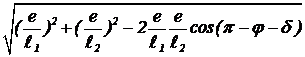 , (12)
, (12)
где j — угол между направлениями складывающихся векторов, Eо(x) — амплитуда. Интенсивность волны I(x) пропорциональна квадрату амплитуды напряженности: 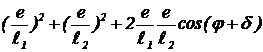 (13)
(13)
Угол между направлениями складывающихся векторов j равен разности фаз вкладов: 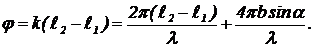 Повторяя вычисления (7) — (8), находим:
Повторяя вычисления (7) — (8), находим: 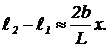 (14)
(14)
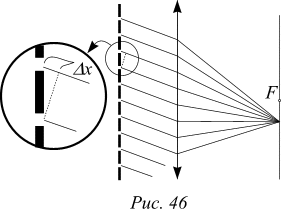
Условие максимума j=2pN, что для положений xmax дает: 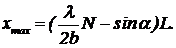 (15) Из формулы (15) следует, что положение каждого из максимумов сдвинуто на L sina.
(15) Из формулы (15) следует, что положение каждого из максимумов сдвинуто на L sina.
 Здесь надо иметь в виду, что при расчетах предполагались малые отклонения от плоскости симметрии установки. Для произвольных отклонений роль L играет величина L/cosa. Это позволяет сделать вывод о том, что дифракционная картина при наклонном падении смещена вниз на Ltga и растянута в 1/cosa раз.
Здесь надо иметь в виду, что при расчетах предполагались малые отклонения от плоскости симметрии установки. Для произвольных отклонений роль L играет величина L/cosa. Это позволяет сделать вывод о том, что дифракционная картина при наклонном падении смещена вниз на Ltga и растянута в 1/cosa раз.
Полученный результат при некоторой модификации может быть использован для решения задачи 3 домашнего задания.
Задача 2. Одна из щелей в описанном выше дифракционном опыте толще другой в q раз, поэтому можно считать, что интенсивность света, попадающего в одну щель, в q раз больше интенсивности света, попадающего в другую щель. Чему равно отношение интенсивностей в первых дифракционных минимуме и максимуме?
2.4 Дифракционная решетка
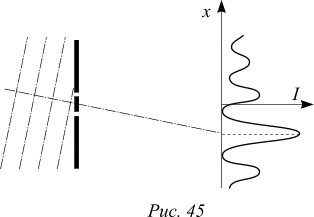
 Рассмотрим прохождение электромагнитной волны через экран с большим числом параллельных щелей, расположенных на одинаковых расстояниях d друг от друга. Свет от решетки проходит затем через линзу, расположенную так, что плоскость наблюдения лежит в ее фокальной плоскости. Заметим, что параллельные лучи собираются в одной точке на фокальной плоскости. Разность фаз параллельных лучей не изменяется при проходе через линзу.
Рассмотрим прохождение электромагнитной волны через экран с большим числом параллельных щелей, расположенных на одинаковых расстояниях d друг от друга. Свет от решетки проходит затем через линзу, расположенную так, что плоскость наблюдения лежит в ее фокальной плоскости. Заметим, что параллельные лучи собираются в одной точке на фокальной плоскости. Разность фаз параллельных лучей не изменяется при проходе через линзу.
Разность хода Dx для вторичных волн, испущенных двумя соседними щелями и распространяющимися под одним и тем же углом j к направлению распространения падающей на решетку волны, равна (рисунок 46)
Dx=d sin j. (16)
При Dx=Nl вторичные волны, испущенные в данном направлении всеми щелями, усиливают друг друга, поэтому направления на максимумы определяются так: 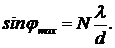 (17)
(17)
Задача 3. Интерференционные картины при дифракции на двух щелях и на дифракционной решетке имеют общие черты. Так, при d=2b положения максимумов и минимумов в обоих случаях совпадают. Объясните, почему дифракционные максимумы при рассеянии на решетке гораздо уже, чем при рассеянии на двух щелях. В промежутках между максимумами интенсивность практически равна нулю.
4. Домашнее задание
4.1 Решение задач
Задача 1. Угол падения плоской электромагнитной волны на экран с двумя щелями составляет 30о. Одна из щелей шире другой в 4 раза. Расстояние между щелями 2b составляет 10 длин волн. Ширина щелей много меньше длины волны. Рассчитайте распределение интенсивности волны на экране, отстоящем от щелей на расстоянии Nb, N>>1, положения нулевого и первого максимумов дифракционной картины.
Задача 2. Домашний опыт. Возьмите грампластинку и, рассматривая отраженный от нее свет, пронаблюдайте дифракцию. Оцените расстояние между бороздками на пластинке. (Лучший эффект получается при использовании компакт-диска.) Результат проконтролируйте независимым измерением.
Задача 3. Как, имея дифракционную решетку с периодом d, получить такую дифракционную картину, как от дифракционной решетки с периодом d/2? Ответ обоснуйте.
ЗАНЯТИе 1.2.4
зоны френеля
2. Дифракция на краю непрозрачного экрана
2.1 Метод векторных диаграмм при анализе дифракции
2.1.1 Дифракция на краю экрана
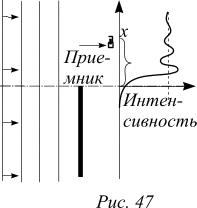 Опыт 1. Электромагнитная волна, излучаемая генератором трехсантиметровых волн, падает на край металлического экрана. Экран не пропускает волну. При перемещении приемника параллельно экрану на некотором отдалении от него регистрируются небольшие ослабления и усиления сигнала.
Опыт 1. Электромагнитная волна, излучаемая генератором трехсантиметровых волн, падает на край металлического экрана. Экран не пропускает волну. При перемещении приемника параллельно экрану на некотором отдалении от него регистрируются небольшие ослабления и усиления сигнала.
Вблизи края тени наблюдается усиление сигнала, превосходящее уровень вдали от края. На рисунке приведен примерный вид зависимости интенсивности сигнала от положения приемника.
2.1.2 Модель фронта плоской волны
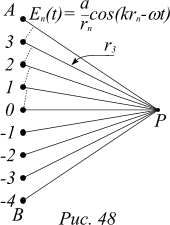 В рассмотренных на предыдущем занятии ситуациях одна, или две, или множество щелей в экране действовали, как излучающие антенны. При исследовании разнообразных физических обстоятельств использование такого подхода часто оказывается плодотворным. Рассмотрим с точки зрения вторичных волн излучение волновой поверхностью плоской волны в некоторую точку P в такой модели.
В рассмотренных на предыдущем занятии ситуациях одна, или две, или множество щелей в экране действовали, как излучающие антенны. При исследовании разнообразных физических обстоятельств использование такого подхода часто оказывается плодотворным. Рассмотрим с точки зрения вторичных волн излучение волновой поверхностью плоской волны в некоторую точку P в такой модели.
Вдоль линии AB на малых расстояниях друг от друга расположены параллельно друг другу работающие и излучающие синхронно антенны. Первая наша задача состоит в предсказании результирующего электрического поля или интенсивности электромагнитной волны в точке P, находящейся на расстоянии L от линии AB. При решении ее будем использовать принцип суперпозиции, согласно которому результирующее электромагнитное поле в данной точке равно геометрической сумме вкладов от каждой антенны. Кроме того, поскольку все вклады в электрическое поле представляют собой гармонические колебания одной и той же частоты, при рассмотрении используем метод векторных диаграмм.
а) Пусть точка P находится на таком расстоянии r0 от цепочки антенн, что фаза вклада в результирующую напряженность электрического поля в данной точке от антенны №0 равна нулю. Колеблющийся по косинусоидальному закону вклад 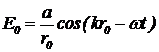 изобразится вектором, вращающимся с угловой скоростью w. Вращение векторов будем наблюдать из вращающейся системы координат. Тогда вклад в напряженность электрического поля от антенны №0 изобразится горизонтальной стрелкой (рисунок 49).
изобразится вектором, вращающимся с угловой скоростью w. Вращение векторов будем наблюдать из вращающейся системы координат. Тогда вклад в напряженность электрического поля от антенны №0 изобразится горизонтальной стрелкой (рисунок 49).
б) От антенны №1 волна проходит немногим большее расстояние. Имеет место запаздывание волны. Фаза вклада от антенны №1 будет чуть-чуть побольше. Вектор, изображающий этот вклад 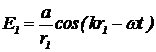 , слегка повернут.
, слегка повернут.
в) Запаздывание фазы колебаний nой “антенны” по сравнению с фазой (n-1)ой — предыдущей — растет по мере удаления от антенны №0 (сравните разности хода на рисунке). По этой причине последовательность складывающихся векторов скручивается в спираль.
Причина, по которой цепочка вкладов скручивается в спираль, а не в окружность, состоит в следующем. С удалением антенн от точки наблюдения амплитуды вкладов уменьшаются и к тому моменту, когда дело дойдет до вклада с отставанием фазы на 2p, даже при равномерном повороте последующих векторов, последний бы не вернулся в исходную точку.
2.1.3 Дифракция на краю непрозрачного экрана
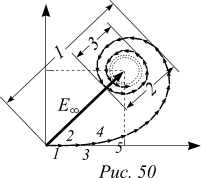 Как уже устанавливалось выше, каждый участок волнового фронта является источником электромагнитной волны, как маленькая антенна. Фронт плоской электромагнитной волны действует как бесконечное множество слившихся, бесконечно тонких антенн, каждая из которых дает бесконечно малый вклад в результирующую волну. Амплитуда результирующего электрического поля складывается из бесконечного числа бесконечно малых векторов. Диаграмма сложения вкладов представляется непрерывной гладкой кривой (спираль Корню). Амплитуда результирующего электрического поля изображается вектором, соединяющим полюсы этой кривой (рисунок 49). Стрелочки вкладов помечены цифрами в соответствии с номерами антенн.
Как уже устанавливалось выше, каждый участок волнового фронта является источником электромагнитной волны, как маленькая антенна. Фронт плоской электромагнитной волны действует как бесконечное множество слившихся, бесконечно тонких антенн, каждая из которых дает бесконечно малый вклад в результирующую волну. Амплитуда результирующего электрического поля складывается из бесконечного числа бесконечно малых векторов. Диаграмма сложения вкладов представляется непрерывной гладкой кривой (спираль Корню). Амплитуда результирующего электрического поля изображается вектором, соединяющим полюсы этой кривой (рисунок 49). Стрелочки вкладов помечены цифрами в соответствии с номерами антенн.
Пусть теперь часть волнового фронта, вплоть до перпендикуляра, опущенного из точки P на фронт, закрыта непрозрачным экраном. В новой ситуации от закрытой части фронта излучение в точку P не попадает (вклады, изображаемые нижней частью кривой). Напряженность результирующего электрического поля теперь равна вектору, проведенному от центра спирали в верхний полюс.


