Методичка по электротехнике — энергообеспечение предприятий
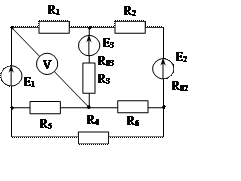
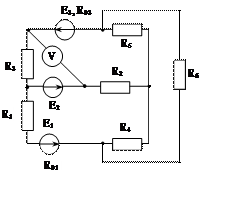
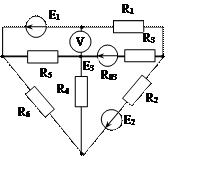
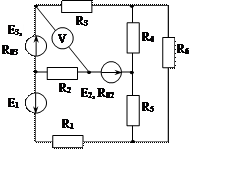
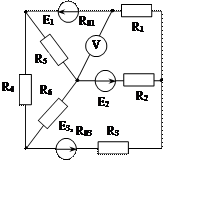
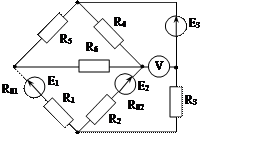
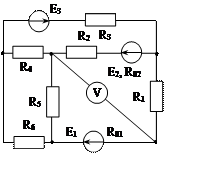
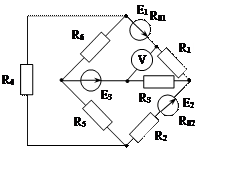
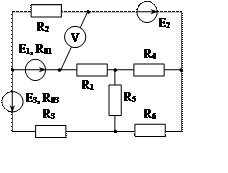
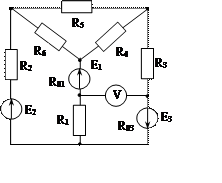
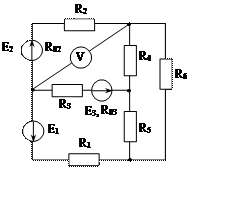
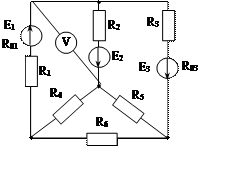
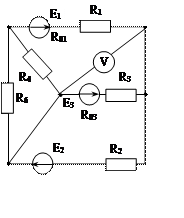
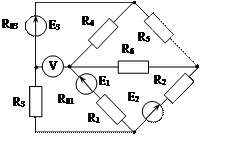
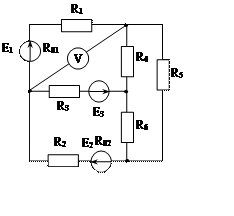
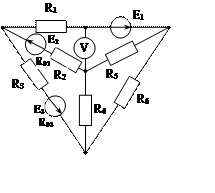
Задача 1. Для эл. цепи, схема которой изображена на рис. 1.1 – 1.50, по заданным в табл. 1 сопротивлениям и эдс выполнить следующее:
1. Составить систему уравнений, необходимых для определения токов по первому и второму законам Кирхгофа;
2. Найти все токи, пользуясь методом контурных токов;
3. Определить токи методом двух узлов, преобразовав треугольник сопротивлений R4R5R6 в эквивалентную звезду;
4. Определить показание вольтметра и составить баланс мощностей для заданной схемы;
5. 
 Построить в масштабе потенциальную диаграмму для внешнего контура.
Построить в масштабе потенциальную диаграмму для внешнего контура.
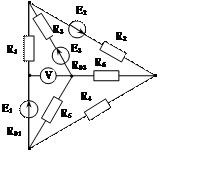 |
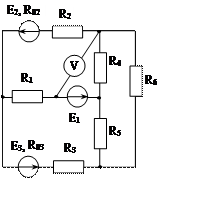
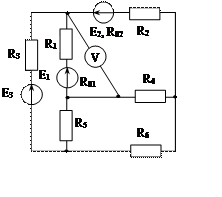 Рис.1.1 Рис. 1.2 Рис. 1.3
Рис.1.1 Рис. 1.2 Рис. 1.3
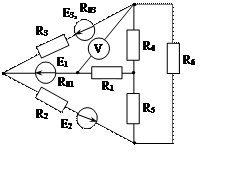 |
Рис. 1.4 Рис. 1.5 Рис. 1.6
 |
 |
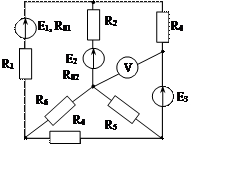 |
Рис. 1.7 Рис. 1.8 Рис. 1.9
 |
 |
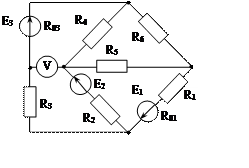 |
Рис. 1.10 Рис. 1.11 Рис. 1.12
 |
 |
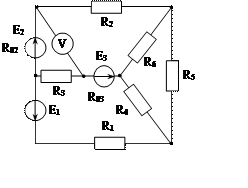 |
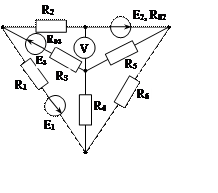 Рис. 1.13 Рис. 1.14 Рис. 1.15
Рис. 1.13 Рис. 1.14 Рис. 1.15
 |
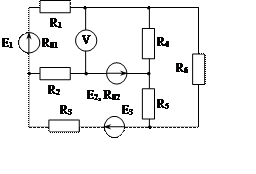 |
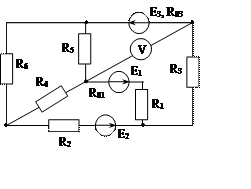
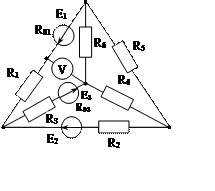
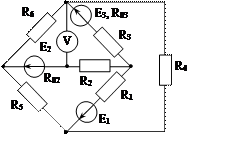 Рис. 1.16 Рис. 1.17 Рис. 1.18
Рис. 1.16 Рис. 1.17 Рис. 1.18
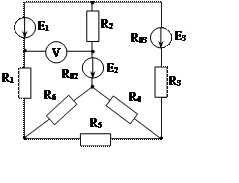
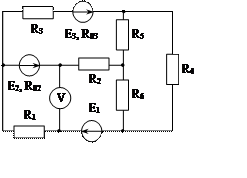
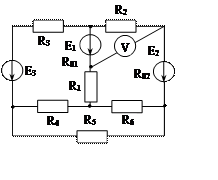 Рис. 1.19 Рис. 1.20 Рис. 1.21
Рис. 1.19 Рис. 1.20 Рис. 1.21
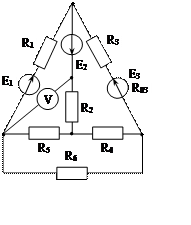 |
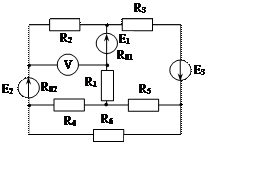
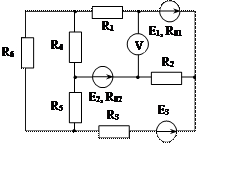 Рис. 1.22 Рис. 1.23 Рис. 1.24
Рис. 1.22 Рис. 1.23 Рис. 1.24
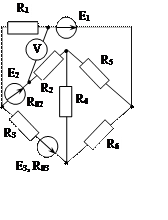 Рис. 1.25 Рис. 1.26 Рис. 1.27
Рис. 1.25 Рис. 1.26 Рис. 1.27
 |
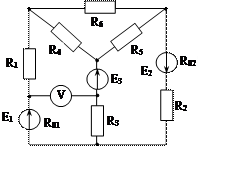 |
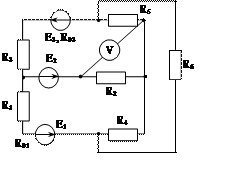
Рис. 1.28 Рис. 1.29 Рис. 1.30
 |
 |
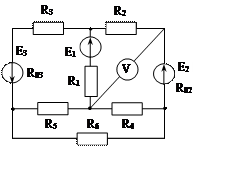 |
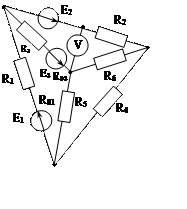
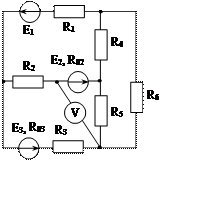
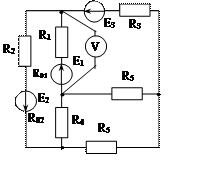
Рис. 1.31 Рис. 1.32 Рис. 1.33
 |
 |
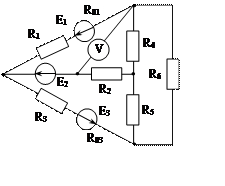 |
Рис. 1.34 Рис. 1.35 Рис. 1.36
 |
 |
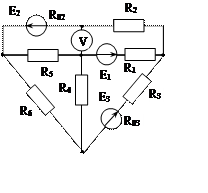 |
Рис. 1.37 Рис. 1.38 Рис. 1.39
 |
 |
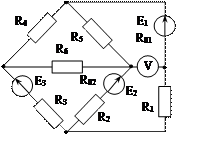 |
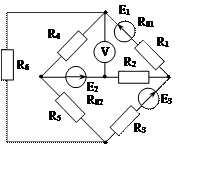
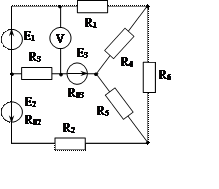
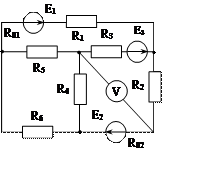 Рис. 1.40 Рис. 1.41 Рис. 1.42
Рис. 1.40 Рис. 1.41 Рис. 1.42
Рис. 1.43 Рис. 1.44 Рис. 1.45
 |
 |
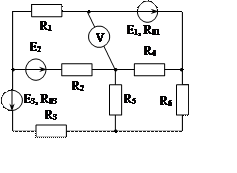 |
Рис. 1.46 Рис. 1.47 Рис. 1.48
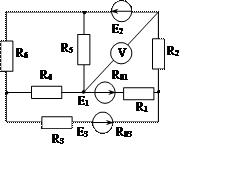 |
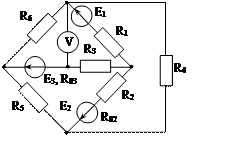 |
Рис. 1.49 Рис. 1.50
Таблица 1
|
Номера |
Е1, В |
Е2, В |
Е3, В |
R01, Ом |
R02, Ом |
R03, Ом |
R1, Ом |
R2, Ом |
R3, Ом |
R4, Ом |
R5, Ом |
R6, Ом |
|
|
варианта |
рисунка |
||||||||||||
|
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 |
1.1 1.2 1.3 1.4 1.5 1.1 1.6 1.7 1.8 1.9 1.10 1.11 1.12 1.13 1.14 1.15 1.16 1.17 1.18 1.19 1.20 1.21 1.22 1.23 1.24 1.25 1.26 1.27 1.28 1.29 1.30 1.31 1.32 1.33 1.34 1.35 1.36 1.37 1.38 1.39 1.40 1.41 1.42 1.43 1.44 1.45 1.46 1.47 1.48 1.49 1.50 |
22 55 36 16 14 20 5 10 6 21 4 4 16 48 12 12 8 72 12 12 9 15 54 36 3 12 30 10 5 40 8 22 55 36 16 14 5 10 6 21 4 4 16 48 12 12 8 72 12 12 9 |
24 18 10 5 25 22 16 6 20 4 9 24 8 12 36 6 6 12 48 30 6 63 27 9 66 30 16 32 10 25 40 24 18 10 5 25 16 6 20 4 9 24 8 12 36 6 6 12 48 30 6 |
10 4 25 32 28 9 30 24 4 10 18 6 9 6 12 40 36 4 6 9 27 6 3 24 9 25 10 10 36 8 10 10 4 25 32 28 30 24 4 10 18 6 9 6 12 40 36 4 6 9 27 |
0,2 0,8 — — 0,9 0,1 0,4 0,8 — — 0,8 0,9 0,2 0,8 — 1,2 1,3 0,7 — 0,5 — 1,0 1,2 — — 1,0 0,6 0,6 0,3 — 0,8 0,2 0,8 — — 0,9 0,4 0,8 — — 0,8 0,9 0,2 0,8 — 1,2 1,3 0,7 — 0,5 — |
— — 0,4 0,6 1,2 — — 0,3 0,8 0,2 — — 0,6 1,4 0,4 0,6 — 1,5 0,4 — 1,0 — 0,9 0,8 0,7 0,4 0,8 — — 0,2 1,0 — — 0,4 0,6 1,2 — 0,3 0,8 0,2 — — 0,6 1,4 0,4 0,6 — 1,5 0,4 — 1,0 |
1,2 0,8 0,5 0,8 — 1,1 0,7 — 1,2 0,6 0,7 0,5 — — 1,2 — 1,2 — 0,4 0,5 0,8 1,2 — 0,8 1,2 — — 1,0 0,8 0,2 — 1,2 0,8 0,5 0,8 — 0,7 — 1,2 0,6 0,7 0,5 — — 1,2 — 1,2 — 0,4 0,5 0,8 |
2 8 4 9 5 1 6 3,5 4 5 2,7 9,0 2,5 4,2 3,5 2,0 3,0 6,0 2,5 3,5 4,5 5,0 8,0 3,0 1,0 1,0 2,0 1,5 1,2 3,0 5,0 2 8 4 9 5 6 3,5 4 5 2,7 9,0 2,5 4,2 3,5 2,0 3,0 6,0 2,5 3,5 4,5 |
1 4 8 3 2 2 4 5 6 7 10 8 6 4 5 3 2 1 1 2 2 3 3 4 4 5 5 6 6 3 3 1 4 8 3 2 4 5 6 7 10 8 6 4 5 3 2 1 1 2 2 |
8 3 3 2 8 6 3 6 4 2 4 1 6 2 1 8 1 10 4 3 8 1 1 2 2 1 3 1 3 2 3 8 3 3 2 8 3 6 4 2 4 1 6 2 1 8 1 10 4 3 8 |
4 2 1 4 2 3 2 6 4 8 8 6 5 12 5 5 6 4 15 3 13 2 4 1 2 1 1 7 2 4 3 4 2 1 4 2 2 6 4 8 8 6 5 12 5 5 6 4 15 3 13 |
10 4 2 1 2 8 5 3 3 1 10 10 10 6 6 7 8 12 2 1 4 12 2 5 7 6 8 1 2 3 2 10 4 2 1 2 5 3 3 1 10 10 10 6 6 7 8 12 2 1 4 |
6 4 7 5 6 4 3 1 3 1 2 4 5 2 9 8 6 4 2 3 3 3 2 1 3 4 5 5 2 2 1 6 4 7 5 6 3 1 3 1 2 4 5 2 9 8 6 4 2 3 3 |
Методические рекомендации по расчету линейных электрических цепей постоянного тока
Метод преобразования схемы
Рассмотрим электрическую цепь, изображенную на рис. 1. Пусть известны величины сопротивлений резисторов r1, r2, r3, r4, r5, r6, э. д. с. Е и ее внутреннее сопротивление r0. Требуется определить токи во всех участках цепи и напряжение, которое покажет вольтметр (сопротивление его бесконечно велико), включенный между точками схемы а и d.
Такие задачи решаются методом свертывания схемы, по которому отдельные участки схемы упрощают и постепенным преобразованием приводят схему к одному эквивалентному (входному) сопротивлению относительно зажимов источника питания. Схема упрощается с помощью замены группы последовательно или параллельно соединенных сопротивлений одним эквивалентным сопротивлением. Так, сопротивления r4 и r5 соединены последовательно и их эквивалентное сопротивление
![]()
Сопротивления r45 и r6 соединены параллельно и, следовательно, их эквивалентное сопротивление 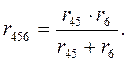
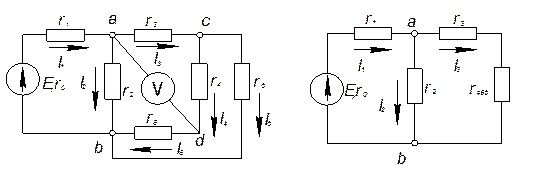
Рис. 1 Рис. 2
После произведенных преобразований цепь принимает вид, показанный на рис. 2, а эквивалентное сопротивление всей цепи найдем из уравнения
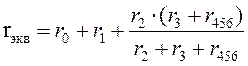 .
.
Ток I1 в неразветвленной части схемы определим по закону Ома:
I1 = E/rэкв.
Воспользовавшись схемой на рис. 2, найдем токи I2 и I3:
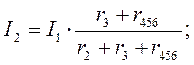
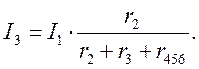
Переходя к рис. 1, определим токи I4, I5 и I6 по аналогичным уравнениям:
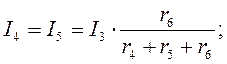
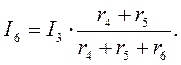
Зная ток I1 можно найти ток I2 другим способом. Согласно второму закону Кирхгофа, Uаb = Е — (r0 + r1) I1, тогда
I2 = Uаb/r2.
Показание вольтметра можно определить, составив уравнение по второму закону Кирхгофа, например, для контура acda:
r3 I3 + r4 I4 = Uаd.
Для проверки решения можно воспользоваться первым законом Кирхгофа и уравнением баланса мощностей, которые для схемы, изображенной на рис. 1, примут вид
I1 = I2 + I3; I3 = I4 + I6;
E•I1 = (r0 + r1)I12 + r2I22 + r3I32 + (r4 + r5)I42 + r6I62.
Законы Кирхгофа
Важным вопросом этого раздела является расчет распределения токов в сложных линейных цепях с несколькими источниками. Классическим методом расчета таких цепей является непосредственное применение законов Кирхгофа. Все остальные методы расчета исходят из этих фундаментальных законов электротехники.
Рассмотрим сложную электрическую цепь (рис. 3), которая содержит 6 ветвей. Если будут заданы величины всех э. д. с. и сопротивлений, а по условию задачи требуется определить токи в ветвях, мы будем иметь задачу с шестью неизвестными. Такие задачи решаются при помощи законов Кирхгофа. В этом случае должно быть составлено столько уравнений, сколько неизвестных токов.
Порядок расчета:
1. Если цепь содержит последовательные и параллельные соединения, ее упрощают, заменяя эти соединения эквивалентными.
2. Произвольно указывают направления токов во всех ветвях. Если принятое направление тока не совпадает с действительным, то при расчете такие токи получаются со знаком “минус”.
3. Составляют (п – 1) уравнений по первому закону Кирхгофа (п — число узлов).
4. Недостающие уравнения составляют по второму закону Кирхгофа, при этом обход контура можно производить как по часовой стрелке, так и против нее. За положительные э. д. с. и токи принимаются такие, направление которых совпадает с направлением обхода контура. Направление действия э. д. с. внутри источника всегда принимают от минуса к плюсу.
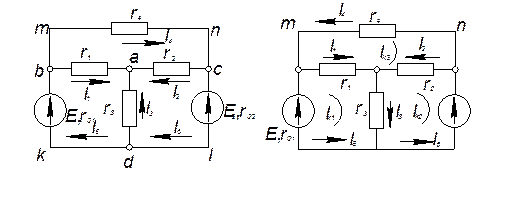
Рис. 3 Рис. 4
5. Полученную систему уравнений решают относительно неизвестных токов. Составим расчетные уравнения для электрической цепи, изображенной на рис. 3. Выбрав произвольно направление токов в ветвях цепи, составляем уравнения по первому закону Кирхгофа для узлов а, b и с:
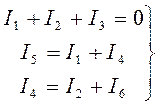 (1)
(1)
Приняв направление оборота контуров по часовой стрелке, составляем уравнения по второму закону Кирхгофа для трех произвольно выбранных контуров:
для контура adkb:
![]() (2)
(2)
для контура bacldkb:
![]() (3)
(3)
для контура bmncab:
![]() (4)
(4)
Решая совместно уравнения (1), (2), (3) и (4), определяем токи в ветвях электрической цепи.
Легко заметить, что решение полученной системы из шести уравнений является весьма трудоемкой операцией.
Метод контурных токов
При расчете сложных электрических цепей целесообразно применить метод контурных токов (метод ячеек), который позволяет уменьшить число уравнений, составляемых по двум законам Кирхгофа, на число уравнений записанных по первому закону Кирхгофа. Следовательно, число уравнений, составляемых по методу контурных токов, равно т — n + 1. При решении методом контурных токов количество уравнений определяется числом ячеек. Ячейкой будем называть такой контур, внутри которого отсутствуют ветви. В нашем случае таких контуров-ячеек три: bаdkb, асlda и mncabm.
Расчет сложных электрических цепей методом контурных токов ведется следующим образом:
1. Вводя понятие «контурный ток», произвольно задаемся направлением этих токов в ячейках. Удобнее все токи указать в одном направлении, например по часовой стрелке (рис. 4) .
2. Составляем для каждого контура-ячейки уравнение по второму закону Кирхгофа. Обход контуров производим по часовой стрелке:
первый контур:
![]() (5)
(5)
второй контур:
![]() (6)
(6)
третий контур:
![]() (7)
(7)
3. Решая совместно уравнения (5), (6), (7), определяем контурные токи. В том случае, когда контурный ток получается со знаком “минус”, это означает, что его направление противоположно выбранному на схеме.
4. Токи во внутренних ветвях схемы определяются как сумма или разность соответствующих контурных токов. В том случае, когда контурные токи в ветви совпадают, берут сумму, а когда направлены навстречу − токи вычитают.
5. Токи во внешних ветвях схемы равны по величине соответствующим контурным токам.
Пример. Рассчитать сложную цепь постоянного тока для схемы, изображенной на рис. 4. Задано: Е1 = 100 В, Е2 = 120 В, r01 = r02 = 0,5 Ом, r1 = 5 Ом, r2 = 10 Ом, r3 = 2 Ом, r4 = 10 Ом. Определить токи в ветвях цепи.
Решение. Используя уравнения (5), (6) и (7), получаем:
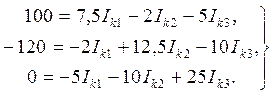
Выразив Ik3 через Ik1 и Ik2:
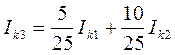
и произведя соответствующие подстановки, получаем:
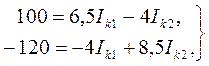
Совместное решение полученных уравнений дает:
![]()
![]()
![]()
Определяем токи в ветвях:
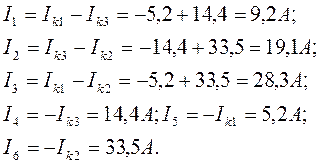
Метод двух узлов
На практике часто используются цепи, в которых параллельно включены несколько источников энергии и приемных устройств. Такие цепи удобно анализировать с помощью метода узлового напряжения (напряжения между двумя узлами).
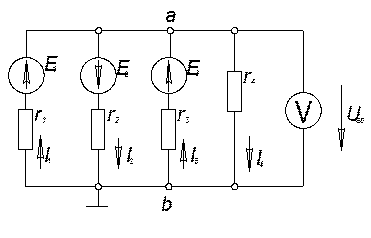
Рис. 5
Пример. Найти токи цепи (рис. 5) и показание вольтметра, если r1 = r2 = r3 = r4 = 10 Ом. Е1 = 10 В, Е2 = 18 В, Е3 = 10 В.
Решение. Найдем узловое напряжение Uab (показание вольтметра):
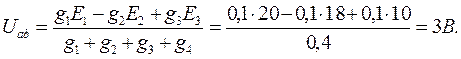
При этом учитываем, что с плюсом записываются эдс, направленные к узлу «а», с минусом – эдс, направленные от узла «а».
Токи в ветвях определяются по закону Ома:
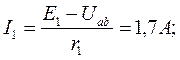
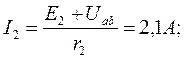
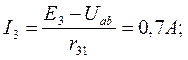
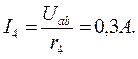
Знаки «плюс» или «минус» выбираются в соответствии с законом Ома для ветви с источником. Если направление э. д. с. и напряжения совпадают с направлением тока, то берется знак «плюс», в противном случае – знак «минус».
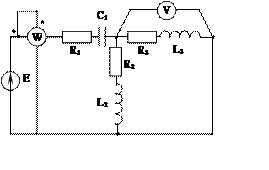
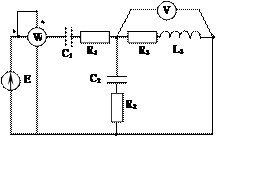
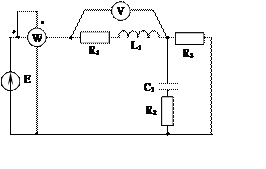
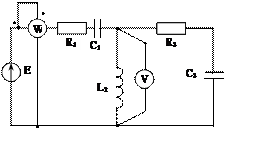
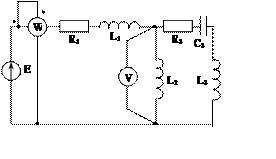
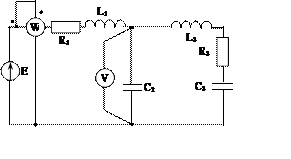
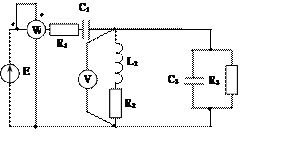
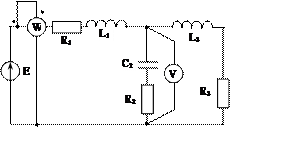
 Задача 2. Для электрической цепи, схема которой изображена на рис. 2.1 – 2.50, по заданным в табл. 2 параметрам и ЭДС источника определить токи во всех ветвях цепи и напряжения на отдельных участках. Составить баланс активной и реактивной мощности. Построить в масштабе на комплексной плоскости векторную диаграмму токов и потенциальную диаграмму напряжений по внешнему контуру. Определить показание вольтметра и активную мощность, измеряемую ваттметром.
Задача 2. Для электрической цепи, схема которой изображена на рис. 2.1 – 2.50, по заданным в табл. 2 параметрам и ЭДС источника определить токи во всех ветвях цепи и напряжения на отдельных участках. Составить баланс активной и реактивной мощности. Построить в масштабе на комплексной плоскости векторную диаграмму токов и потенциальную диаграмму напряжений по внешнему контуру. Определить показание вольтметра и активную мощность, измеряемую ваттметром.
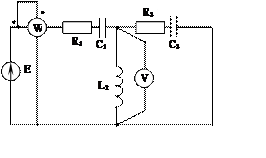
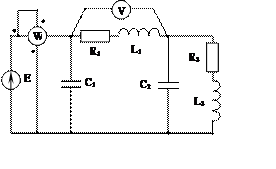
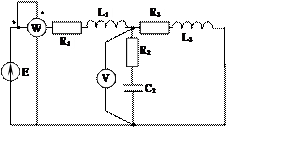 Рис. 2.1 Рис. 2.2 Рис. 2.3
Рис. 2.1 Рис. 2.2 Рис. 2.3
Рис. 2.4 Рис. 2.5 Рис. 2.6
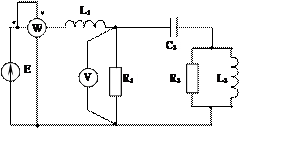 |
 |
 |
|
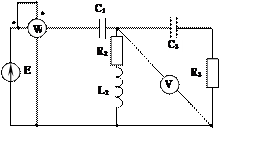
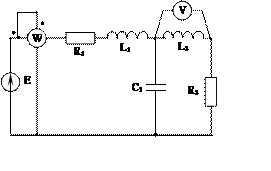
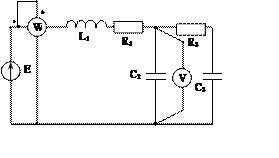 Рис. 2.7 Рис. 2.8 Рис. 2.9
Рис. 2.7 Рис. 2.8 Рис. 2.9
Рис. 2.10 Рис. 2.11 Рис. 2.12
 |
 |
 |
Рис. 2.13 Рис. 2.14 Рис. 2.15
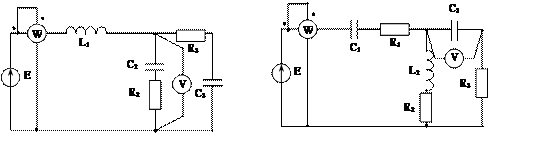 |
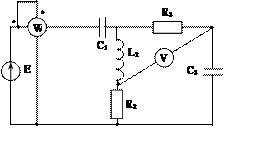 |
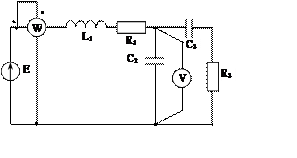
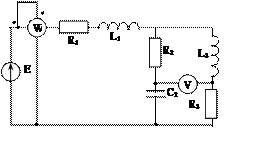
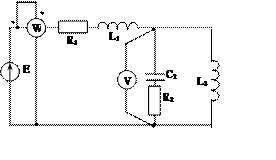 Рис. 2.16 Рис. 2.17 Рис. 2.18
Рис. 2.16 Рис. 2.17 Рис. 2.18
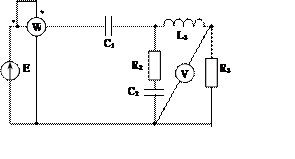
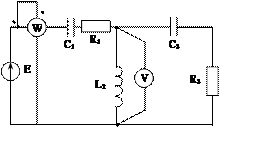
 Рис. 2.19 Рис. 2.20 Рис. 2.21
Рис. 2.19 Рис. 2.20 Рис. 2.21
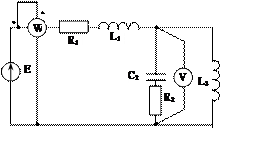
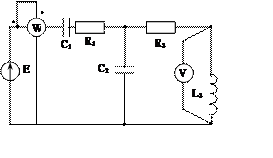
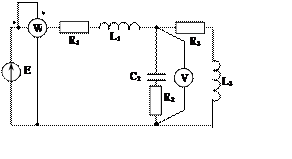 Рис. 2.22 Рис. 2.23 Рис. 2.24
Рис. 2.22 Рис. 2.23 Рис. 2.24
Рис. 2.25 Рис. 2.26 Рис. 2.27
 |
 |
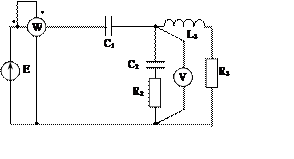 |
Рис. 2.28 Рис. 2.29 Рис. 2.30
 |
 |
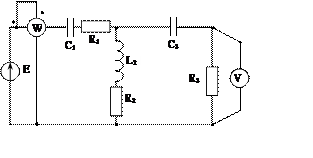 |
Рис. 2.31 Рис. 2.32 Рис. 2.33
 |
|
 |
 |
Рис. 2.34 Рис. 2.35 Рис. 2.36
 |
 |
 |
|
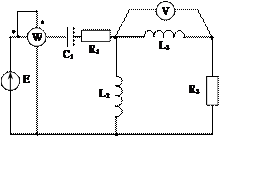
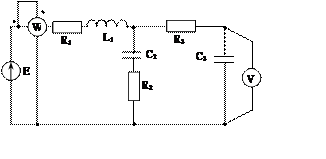
 Рис. 2.37 Рис. 2.38 Рис. 2.39
Рис. 2.37 Рис. 2.38 Рис. 2.39
Рис. 2.40 Рис. 2.41 Рис. 2.42
 |
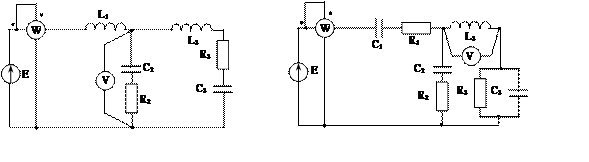 |
Рис. 2.43 Рис. 2.44 Рис. 2.45
 |
 |
 |
Рис. 2.46 Рис. 2.47 Рис. 2.48
 |
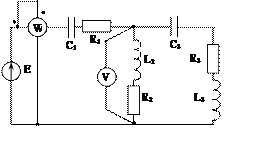 |
Рис. 2.49 Рис. 2.50
Таблица 2
|
Номера |
Е, В |
f, Гц |
С1, мкФ |
С2, мкФ |
С3, мкФ |
L1, мГн |
L2, мГн |
L3, мГн |
R1, Ом |
R2, Ом |
R3, Ом |
|
|
Вари-анта |
Рис. |
|||||||||||
|
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 |
2.1 2.2 2.3 2.4 2.5 2.1 2.6 2.7 2.8 2.9 2.10 2.11 2.12 2.13 2.14 2.15 2.16 2.17 2.18 2.19 2.20 2.21 2.22 2.23 2.24 2.25 2.26 2.27 2.28 2.29 2.30 2.31 2.32 2.33 2.34 2.35 2.36 2.37 2.38 2.39 2.40 2.41 2.42 2.43 2.44 2.45 2.46 2.47 2.48 2.49 2.50 |
150 100 120 200 220 50 100 120 200 220 50 100 120 200 220 150 100 120 200 220 50 100 120 200 220 150 100 100 200 220 50 100 120 200 220 50 100 150 200 220 50 100 120 200 220 50 100 120 200 220 50 |
50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 |
637 — 637 — 637 100 100 — — — — 637 — — 637 100 — 100 637 — — — — 637 637 — 637 — — 637 318 318 — 318 318 — 637 637 — — 637 — 500 500 — 500 500 — 318 318 — |
300 — — 300 — 159 300 — 159 318 637 — 300 — — — 1600 — — 1600 159 159 159 159 159 159 159 159 159 — 637 — — — — 318 — — 318 — — 318 — — 318 159 — 159 318 — 318 |
— 100 — — 100 — — 100 — — — 100 100 100 200 200 200 200 200 — — 200 200 200 — — 637 — 637 637 — 300 300 300 300 — 200 200 200 200 200 200 — 159 159 159 — — 159 159 — |
— 15,9 — 15,9 — — 15,9 15,9 — 15,9 15,9 — 31,8 31,8 — — 31,8 — — 31,8 31,8 15,9 15,9 — — 25 — 25 25 — — — 19,1 — — 19,5 — — 15,9 15,9 — 9,55 — — 9,55 — — 15,9 — — 15,9 |
— 9 15,9 — 47,7 — — — — — — 15,7 — — 15,9 15,9 — 15,9 31,8 — — — — 31,8 — — — — — 9 — — 15,9 15,9 15,9 — 31,8 31,8 — 31,8 31,8 — 15,9 15,9 — — 15,9 — — 31,8 — |
15,9 15,9 15,9 15,9 — 115 115 115 115 — 6,37 — — — — — — — — 95 95 — — 95 95 95 95 95 95 — 31,8 31,8 31,8 31,8 31,8 31,8 95 — 95 95 95 — 95 — 95 31,8 31,8 31,8 31,8 31,8 31,8 |
2 8 8 8 8 10 10 — 10 10 5 — 5 5 5 10 — 10 — 10 15 15 — 15 — 6 6 6 6 6 — — 40 10 — 8 8 8 8 8 4 4 4 40 — 35 35 35 35 35 5 |
3 3 3 3 — 4 — 4 4 4 — 10 — 10 10 2 8 8 8 8 10 — 10 10 10 10 — 4 — — 10 10 — 10 10 10 — 10 — — 40 40 — 10 10 20 — 20 20 20 10 |
4 4 4 4 4 100 100 100 100 100 8 8 8 8 8 10 10 10 10 — 10 10 20 20 20 20 20 — 20 20 40 10 10 40 10 4 4 4 4 4 40 4 4 40 40 40 40 80 80 80 80 |
Методические рекомендации по расчету цепей синусоидального тока
Пример. Рассчитать электрическую цепь синусоидального тока со смешанным соединением приемников. Для схемы, изображенной на рис. 6, известно, что
U = 120 B, r1 = 10 Ом, r2 = 24 Ом, r3 = 15 Ом,
L1 = 19,1 мГ, L3 = 63,5 мГ, С2 = 455 мкФ, f = 50 Гц.
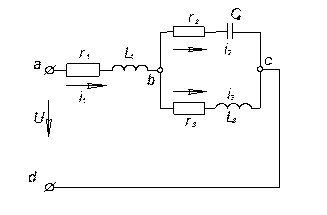
Рис. 6
Определить токи ![]() в ветвях цепи, напряжения на участках цепи
в ветвях цепи, напряжения на участках цепи ![]() , активную, реактивную и полную мощности и построить векторную диаграмму.
, активную, реактивную и полную мощности и построить векторную диаграмму.
Решение. Выражаем сопротивления ветвей цепи в комплексной форме:
Z = r ± jx = ze+jφ;
Z1 = r1+jωL1 = 10+j2π•50•19,1•10-3 = 10+j6 Ом.
Переходя от алгебраической формы записи комплексного числа к показательной, получаем: Z1 = z1e jφ1 = 11,6e j31˚ Ом,
где ![]()
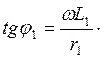
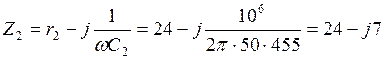 Ом = 25e-j16˚ 15′ Ом;
Ом = 25e-j16˚ 15′ Ом;
Z3 = r3+jωL3 = 15+j2π•50•63,5•10-3 = 15+j20 Ом =25e j53˚ 05′ Ом.

Рис. 7
Выражаем заданное напряжение U в комплексной форме. Если начальная фаза напряжения не задана, то её можно принять равной нулю и располагать вектор напряжения совпадающим с положительным и направлением действительной оси. В этом случае мнимая составляющая комплексного числа будет отсутствовать (рис. 7):
![]() = U = 220 В.
= U = 220 В.
Полное комплексное сопротивление цепи
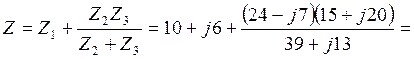
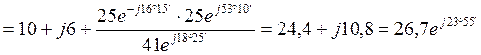 Ом.
Ом.
Определяем ток![]() в неразветвленной части цепи:
в неразветвленной части цепи:
![]()
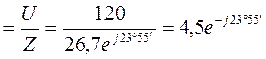 A.
A.
Токи ![]() и
и ![]() в параллельных ветвях могут быть выражены через ток в неразветвленной части цепи:
в параллельных ветвях могут быть выражены через ток в неразветвленной части цепи:
![]() =
= ![]()
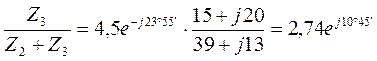 A;
A;
![]() =
=![]()
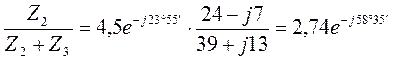 A.
A.
Токи ![]() и
и ![]() можно найти и по-другому:
можно найти и по-другому:
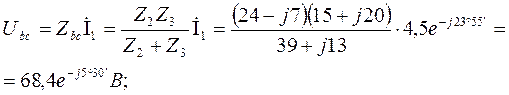
![]()
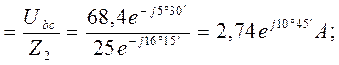
![]()
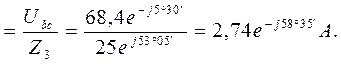
Найдем мощности всей цепи и отдельных её ветвей:
![]()
Для определения активной и реактивной мощностей полную мощность, выраженную комплексным числом в показательной форме, переводим в алгебраическую форму. Тогда действительная часть комплекса будет представлять собой активную мощность, а мнимая – реактивную:
![]()
откуда
Р = 494 Вт; Q = 218 вар.
Активную и реактивную мощности можно найти и по-другому:
Р = Re![]() Вт;
Вт;
![]() Вт;
Вт; ![]() Вт;
Вт;
![]() Вт.
Вт.
Проверка показывает, что Р = Р1 + Р2 + Р3.
![]() = 120 • 4,5 sin 23˚55′ = 218 вар;
= 120 • 4,5 sin 23˚55′ = 218 вар;
![]() вар;
вар; ![]() вар;
вар;
![]() вар.
вар.
Учитывая, что Q1 и Q3 положительны (реактивная мощность индуктивных катушек), а Q2 отрицательно (реактивная мощность конденсатора), получим
Q = Q1 – Q2 + Q3 = 218 вар.
На рис. 8 приведена векторная диаграмма токов и напряжений, построенная по расчетным данным. Порядок её построения следующий: по результатам расчетов отложены векторы токов ![]()
![]() и
и![]() , затем по направлению
, затем по направлению ![]() отложен вектор
отложен вектор ![]() и перпендикулярно к нему в сторону опережения – вектор
и перпендикулярно к нему в сторону опережения – вектор![]() . Их сумма дает вектор Z1
. Их сумма дает вектор Z1![]() . Далее в фазе с
. Далее в фазе с ![]() построен вектор
построен вектор ![]() и перпендикулярно к нему в сторону отставания вектор
и перпендикулярно к нему в сторону отставания вектор ![]() , а их сумма дает вектор напряжения на параллельном участке Ubc. Тот же вектор может быть получен, если в фазе с
, а их сумма дает вектор напряжения на параллельном участке Ubc. Тот же вектор может быть получен, если в фазе с ![]() отложить
отложить ![]() и к нему прибавить вектор
и к нему прибавить вектор ![]() , опережающий
, опережающий ![]() на 900. Cумма векторов Z1
на 900. Cумма векторов Z1![]() и Ubc дает вектор приложенного напряжения U.
и Ubc дает вектор приложенного напряжения U.
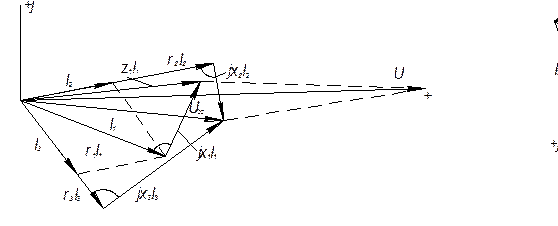 Рис. 8
Рис. 8
Вопросы для подготовки к экзамену по электротехнике
(для студентов специальности ЭОП)
1. Дать определение электрической цепи и ее основных элементов, эквивалентной схемы замещения (модели) реальной электроустановки. Объяснить физическую суть активного, индуктивного и емкостного сопротивлений.
2. 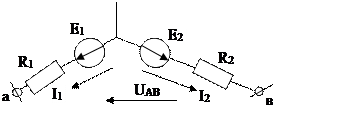 Дать определения понятий ЭДС, напряжения, тока. Выразить напряжение UАВ через величины Е1, Е2 и токи I1 и I2 для заданной цепи, объяснить.
Дать определения понятий ЭДС, напряжения, тока. Выразить напряжение UАВ через величины Е1, Е2 и токи I1 и I2 для заданной цепи, объяснить.
3. Схемы замещения источников энергии. Источники ЭДС, источники тока как схемы замещения реальных источников энергии, их свойства, характеристики, переход от одной схемы к другой.
4. 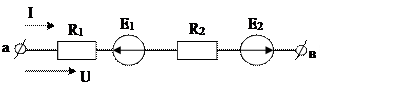 Объяснить применение закона Ома для участка цепи с ЭДС. Вывести формулы для расчета тока в заданной цепи.
Объяснить применение закона Ома для участка цепи с ЭДС. Вывести формулы для расчета тока в заданной цепи.
5. 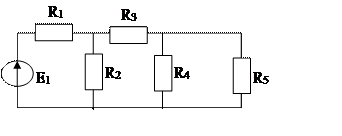 Показать на примере заданной схемы метод расчета простейшей цепи (преобразования схемы).
Показать на примере заданной схемы метод расчета простейшей цепи (преобразования схемы).
6. 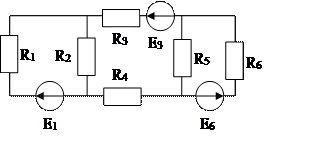 Дать определения законов Кирхгофа для электрической цепи. Объяснить методику расчета электрической цепи непосредственным применением законов Кирхгофа на примере заданной схемы.
Дать определения законов Кирхгофа для электрической цепи. Объяснить методику расчета электрической цепи непосредственным применением законов Кирхгофа на примере заданной схемы.
7. Метод контурных токов. Показать вывод обобщенных уравнений на примере заданной цепи.
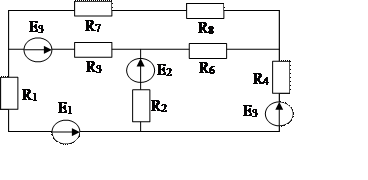 |
8. 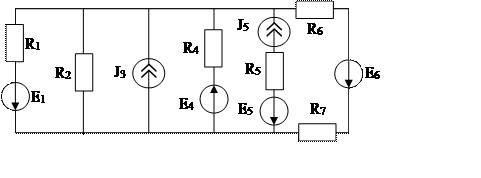 Показать расчет токов в ветвях заданной цепи методом двух узлов.
Показать расчет токов в ветвях заданной цепи методом двух узлов.
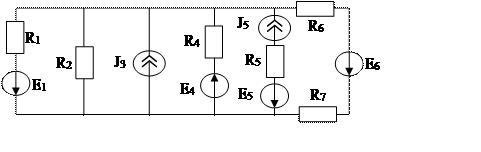 |
9.  Показать последовательность расчета токов в электрической цепи с преобразованием схем треугольника и звезды на примере заданной схемы.
Показать последовательность расчета токов в электрической цепи с преобразованием схем треугольника и звезды на примере заданной схемы.
10. Основные понятия синусоидальной функции электрической величины: амплитуда, начальная фаза, угловая частота. Определить мгновенного значение тока 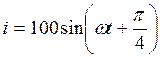 (для времени
(для времени 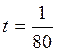 с, если f = 50 Гц).
с, если f = 50 Гц).
11. Дать определение действующим и средним значениям электрических величин. Вывести формулы для определения этих значений через амплитудное значение. Дать определение и доказать числовое значение коэффициентов амплитуды и формы кривой для синусоидальных величин.
12. Объяснить назначение и способ построения волновых диаграмм электрических величин. Определить сдвиг по фазе двух синусоидально изменяющихся величин 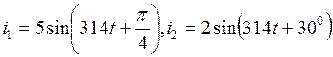 . Изобразить графически.
. Изобразить графически.
13. Объяснить назначение и метод построения векторных диаграмм. Найти с помощью векторной диаграммы ток в неразветвленной части цепи, если к узлу подходят два тока 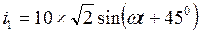 А,
А, 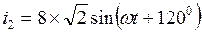 А.
А.
14. Описать процесс в цепи с активным сопротивлением, включенной к источнику синусоидальной ЭДС. Изобразить зависимости рассматриваемых величин в функции времени (волновая диаграмма), построить векторную диаграмму.
15. Описать процесс в цепи с индуктивностью, подключенной к источнику синусоидальной ЭДС. Дать определение и объяснить физическую суть индуктивного сопротивления, угла сдвига фазы между током и напряжением. Построить зависимости тока, напряжения и мощности на индуктивности в функции времени (волновые диаграммы) и векторную диаграмму.
16. Описать процесс с емкостью, подключенной к источнику синусоидального напряжения. Дать определение и объяснить физическую суть емкостного сопротивления, угла сдвига фаз между током и напряжением. Построить зависимости тока, напряжения, мощности на емкости в функции времени (волновая диаграмма) и векторную диаграмму.
17. Используя второй закон Кирхгофа и соотношения между напряжением и током на элементах R, L, С вывести формулу для расчета полного сопротивления цепи с последовательно соединенными элементами R, L, С. Построить векторную диаграмму напряжений этой цепи.
18. Используя первый закон Кирхгофа и соотношения между напряжениями и токами на элементах R, L, С вывести формулу для расчета полной проводимости цепи переменного тока с параллельно соединенными элементами R, L, С. Построить векторную диаграмму токов этой цепи.
19. Дать определение резонанса напряжений, математического выражения условия его существования. Особенности режима цепи при резонансе: ток, напряжение, cosφ, векторная диаграмма цепи. Добротность контура.
20. Дать определение резонанса токов, изобразить векторные диаграммы токов в режиме резонанса для цепи с идеальными L и С; для цепи, где последовательно с L и С включены активные сопротивления. Изобразить частотные характеристики для цепи с резонансом токов, показать практическое использование режима резонанса в электроэнергетике.
21. Дать объяснения понятия коэффициента мощности, формулу определения и способы повышения его величины.
22. Изображение синусоидальных электрических величин в виде векторов и комплексных чисел. Объяснить сущность, целесообразность такого представления синусоидальных электрических величин.
23.  Сопротивление, проводимость в комплексной форме неразветвленной цепи треугольники сопротивлений и проводимостей рассчитать комплексное сопротивление заданной цепи. L1 = 0,03 Гн, С2 = 200 мкФ
Сопротивление, проводимость в комплексной форме неразветвленной цепи треугольники сопротивлений и проводимостей рассчитать комплексное сопротивление заданной цепи. L1 = 0,03 Гн, С2 = 200 мкФ
R1 = 10 Ом, R2 = 15 Ом,
R3 = 10 Ом, f = 50 Гц,
L2 = 0,03 Гн.
24. Комплексная мощность: полная, реактивная, активная составляющие. Треугольник мощностей. Соотношение между составляющими комплексной мощности для последовательной и параллельной схем замещения. Баланс мощности в цепях.
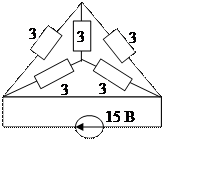
25.  Топографическая диаграмма: определение, методики построения, применение. С помощью топографической и векторной диаграмм определить в заданной цепи токи I1 и I2 и напряжение на входе
Топографическая диаграмма: определение, методики построения, применение. С помощью топографической и векторной диаграмм определить в заданной цепи токи I1 и I2 и напряжение на входе ![]() 1, если ток İ3 = 1 А. Значения сопротивлений в Омах указаны на схеме.
1, если ток İ3 = 1 А. Значения сопротивлений в Омах указаны на схеме.
26. С помощью топографической диаграммы определить напряжение в заданной схеме, если параметры элементов цепи заданы в Омах, а ![]() ав = 100 В.
ав = 100 В.
 |
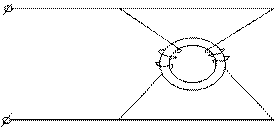
27. Дать определение цепи с взаимоиндукцией, одноименных зажимов индуктивно связанных элементов. Метод экспериментального определения одноименных зажимов. Составить эквивалентную схему замещения заданной цепи.
 |
28. Последовательное соединение индуктивно связанных элементов цепи. Уравнения и сопротивления цепи в комплексной форме. Топографическая диаграмма, емкостный эффект.
29. Уравнения, сопротивления, векторная и топографическая диаграмма цепи с параллельным соединением индуктивно связанных элементов цепи.
30. Составить систему уравнений по законам Кирхгофа для расчета токов в заданной цепи с индуктивными связями.
 |
31. Принцип работы, схема замещения, уравнения и векторная диаграмма трансформаторов без ферромагнитного сердечника.
32. Обосновать метод преобразования двух индуктивно – связанных элементов, присоединенных к одному узлу в эквивалентную схему без индуктивной связи.
33. 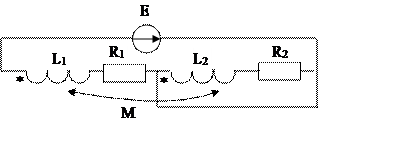 Определить входное сопротивление заданной цепи, применив при расчете эквивалентную замену индуктивных связей электрическими.
Определить входное сопротивление заданной цепи, применив при расчете эквивалентную замену индуктивных связей электрическими.
34. Основные понятия о четырехполюснике, назначение, схема, основные формы записи уравнений четырехполюсника.
35. Дать вывод математической связи между коэффициентами четырехполюсника и параметрами П и Т образными схемами замещения.
36. Составить формулу расчета постоянных четырехполюсника по данным опытов холостого хода и короткого замыкания при включении источника к первым зажимам и опыта короткого замыкания при подключении источника ко вторым зажимам.
37. Методика построения круговой диаграммы активного двухполюсника. Определение электрических величин по элементам диаграмм. Расчет масштабов электрических величин.
38. Методика построения круговой диаграммы четырехполюсника. Определение электрических величин по элементам диаграмм. Расчет масштабов электрических величин.
39. Нелинейные электрические цепи. Свойства нелинейных элементов и их характеристики. Статические и дифференциальные сопротивления. Замена нелинейного сопротивления эквивалентным линейным и ЭДС.
40. Расчет простейших нелинейных цепей при их последовательном, параллельном и смешенном соединениях
41. Магнитные свойства веществ. Основные характеристики, свойства магнитных материалов и величин (В, Н, μ).
42. Магнитные цепи. Определения. Законы магнитных цепей. (Законы полного тока, Ома, Кирхгофа).
43.
|
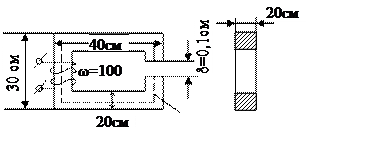 Расчет неразветвленных магнитных цепей. Прямая задача. На примере магнитной цепи (из стали (Э).
Расчет неразветвленных магнитных цепей. Прямая задача. На примере магнитной цепи (из стали (Э).
В(Тл)
|
|
|||||||
100 300 500 Н,![]()
44. 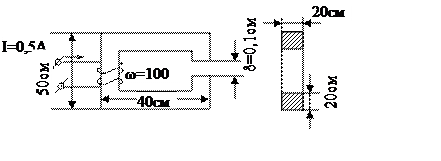 Расчет неразветвленных магнитных цепей. Обратная задача на примере заданной цепи. Материал – электротехническая сталь (Э).
Расчет неразветвленных магнитных цепей. Обратная задача на примере заданной цепи. Материал – электротехническая сталь (Э).
Требования к оформлению контрольной работы:
1. Вариант контрольной работы выбирается по двум последним цифрам учебного шифра студента.
2. На титульном листе контрольной работы должны быть указаны: шифр; дисциплина; фамилия, имя, отчество; курс; факультет; специальность.
3. Работы, оформленные небрежно, вызывающие затруднения при их чтении, возвращаются студенту для переработки.
4. На страницах оставлять поля шириной не менее трех сантиметров для замечаний рецензента.
5. Все расчеты должны сопровождаться краткими пояснениями.
6. Схемы, векторные диаграммы, графики должны быть выполнены в соответствии с требованиями ЕСКД.
7. Работа должна быть подписана с указанием даты ее завершения.
Литература
а) Основная литература
1. Бессонов Л. А. Теоретические основы электротехники, 1ч. — М.: Высшая школа, 2001г.
2. Теория электрических цепей / Под ред. Зевеке Г. В. — М.: 1990.
3. Бессонов Л. А. Сборник задач по ТОЭ. — М.: 2001г.
4. Шебес М. Р. Задачник по ТОЭ. — М.: 2003г.
б) Дополнительная литература
1.Попов В. П. Основы теории цепей. — М.: Высшая школа,1995г.
2. Атабеков Г. И. Теоретические основы электротехники 1,2 ч. — М.: 1978г.
3.Панфилов Д. И., Иванов В. С., Чепурин И. Н. Электротехника и электроника в экспериментах и упражнениях. Практикум на Electronics Workbench. т.1. — М.: 2001г.
4.Прянишников Д. И., Петров Е. А., Осипов Ю. М. Электротехника и ТОЭ в примерах и задачах. — Санкт-Петербург: 2001г.



