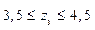Методичка по сопротивлению материалов

ВВЕДЕНИЕ

Сопротивление материалов – это наука об инженерных методах расчетов элементов машин и конструкций на прочность, жесткость и устойчивость. В сопротивлении материалов широко применяются методы теоретической механики и математики, а также используются данные из разделов физики, в которых изучаются различные свойства материалов. Изучение дисциплины сопротивление материалов следует начать с основных понятий, таких как: расчетная схема и составляющие ее элементы: стержни, оболочки, пластины и массивные тела. При расчетах стержневых конструкций следует вспомнить сведения, изучаемые в курсе статики, а именно виды опор: шарнирные подвижные и неподвижные, глухая заделка, а также вспомнить какие реакции возникают в каждом виде этих опор. Необходимо усвоить, что сопротивление материалов решает три основных задачи: проверочный расчет, проектный расчет, определение грузоподъемности. При решении этих задач основным методом сопротивления материалов является метод сечений, когда проводится сечение тела некоторой поверхностью, и после ввода внутренних сил между разрезанными частями, рассматривается равновесие одной из частей. Необходимо запомнить, что в общем случае нагружения в поперечном сечении стержня может возникать шесть внутренних силовых факторов: нормальная сила, две поперечных силы, два изгибающих момента и крутящий момент. Следует обратить внимание на то, что конструкции могут быть как статически определимые (решаемые при помощи статики), так и статически неопределимые (решаемые при помощи уравнений совместности деформаций).

Указания к задаче 1

Для исследования прочности любого тела необходимо знать величину внутренних сил, возникающих в данном теле под действием на него внешних сил. Для определения внутренних сил в сопротивлении материалов используют метод сечений. В общем случае произвольного нагружения стержня в его поперечных сечениях могут возникать шесть внутренних силовых факторов:

  усилие вдоль оси z — продольная сила N;

  усилия вдоль осей х и у — поперечные силы Qx и Qy соответственно;

  момент относительно продольной оси z — крутящий момент МzºТкр;

  моменты относительно осей х и у — изгибающие моменты Мх и My соответственно.

Так как существует шесть внутренних силовых факторов, то при решении пространственных задач необходимо составлять шесть уравнений равновесия:

.

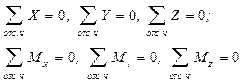Для определения опасного сечения, то есть сечения, в котором внутренние силы имеют наибольшую по абсолютному значению величину, необходимо строить эпюры.

Эпюрой внутренней силы называется график, отображающий изменение внутренней силы по длине бруса, при переходе от одного поперечного сечения к другому.

ПРИМЕР

Для стержня изображенного на рис. 1а определить внутренние силовые факторы в произвольном поперечном сечении и их построить эпюры. F1 = 100 Н, F2 = 300 Н, q = 75 Н/м, a = 0,3 м, b = 0,2 м, l = 2 м.

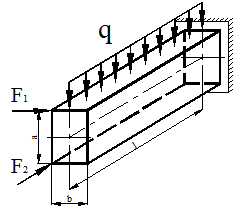
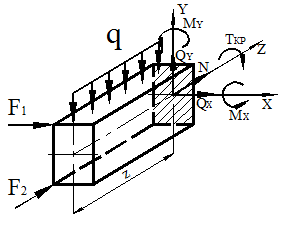
а) б)

Рисунок 1.

Решение.

Рассекаем брус на произвольном расстоянии z от его свободного конца. Отбрасываем правую часть. Располагаем оси координат в центре тяжести сечения. Действие правой части бруса на его левую часть заменяем внутренними силами: N, Qx, Qy, Mx, My, Ткр (рис. 1 б).

Уравновешиваем, то есть, записываем уравнения равновесия и определяем значения внутренних силовых факторов.

;

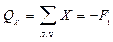QX = — 100Н.

;

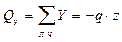при z = 0 Qy = 0;

при z = l Qy = —150 Н.

;

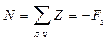N = — 300Н.

;

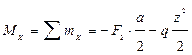при z = 0 Mx = — 45 Н×м;

при z = l Mx = —195 Н×м.

;

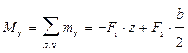при z = 0 My = 30 Н×м; при z = l My = — 170 Н×м.

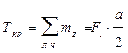; Ткр = 15 Н×м.

Строим эпюры внутренних силовых факторов (рис 2). Опасное сечение в данном брусе будет находиться в заделке, так как в этом сечении значения всех В. С.Ф. имеют наибольшие величины.

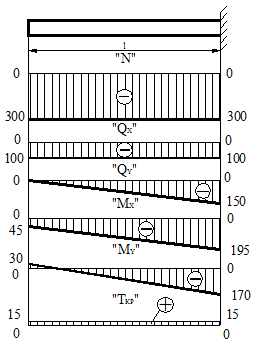
Рисунок 2.

Указания к задаче 2

Растяжением называется такой вид деформации, при котором в поперечном сечении бруса, возникает единственный внутренний силовой фактор – продольная сила.

Для правильного составления уравнений равновесия, при действии на стержень продольной силы, необходимо знать правило знаков, представленное на рис. 3.

Нормальные напряжения при растяжении-сжатии определяются по формуле:

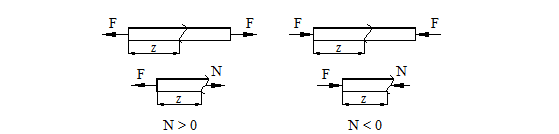
Рисунок 3.

,

где S – площадь поперечного сечения стержня.

Условие прочности выглядит следующим образом:

.

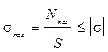Деформации при растяжении-сжатии (абсолютное удлинение) определяется по формуле:

,

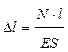где l – длина стержня;

Е – модуль упругости первого рода.

Условие жесткости определяется неравенством вида:

.

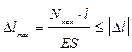ПРИМЕР

Для схемы, изображенной на рис. 4, построить эпюру нормальной силы и определить удлинение стержня, если F1 = 100 кН, F2 = 50 кН, q = 40 кН/м, а= = 1 м, b = 2 м, с = 1,5 м, Е = 2×105 МПа, S = 0,2 м2.

Решение

Разбиваем брус на участки АВ, ВС, CD

Определяем значение нормальной силы на каждом участке

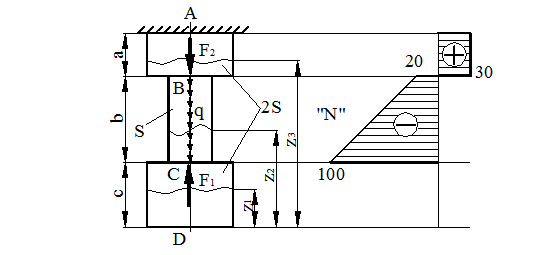
Рисунок 4.

CD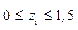

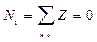
CB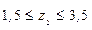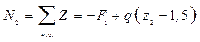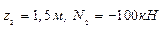

при , при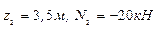

BА