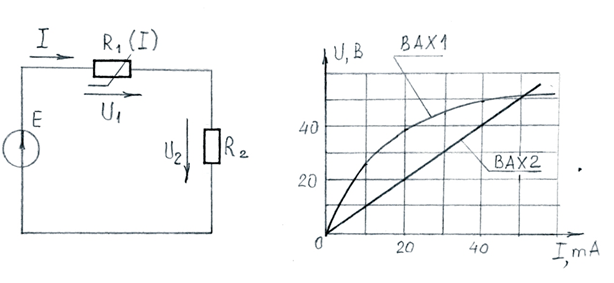
Методы расчета электрических цепей постоянного тока
1.8. Методы расчета электрических цепей постоянного тока.
Закон Ома применяется, как правило, для расчета значения электрических величин на отдельных пассивных и активных участках цепи; законы Кирхгофа применяются при расчете более сложных электрических цепей.
Метод контурных токов – широко распространенный метод расчета сложных электрических цепей с несколькими контурами и с несколькими источниками электрической энергии.
В основе этого метода лежат законы Кирхгофа и 2 предположения:
— в каждом контуре протекают независимые друг от друга расчетные токи, называемые контурными;
— ток в каждой ветви равен алгебраической сумме контурных токов, замыкающихся через эту ветвь. Для проверки правильности вычисления токов в каждой ветви составляется баланс мощности для электрической цепи: мощность, развиваемая источниками электрической энергии, равна мощности всех приемников цепи.
Решить задачу.
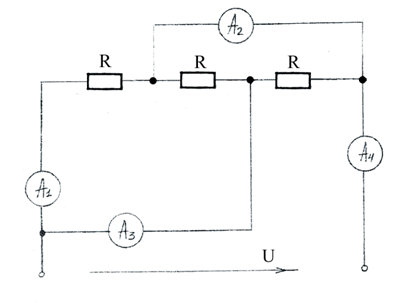
Задача 1.9.
Используя метод контурных токов, найти показания амперметров А1, А2, А3, А4, если R = 30 Ом, U = 150 В.
Метод двух узлов применяется для расчета электрических цепей (участков) с двумя узлами, между которыми включены параллельно активные и пассивные ветви. По расчетной формуле определяется напряжение между узлами, а затем по закону Ома рассчитывается токи в ветвях.
Решить задачу.
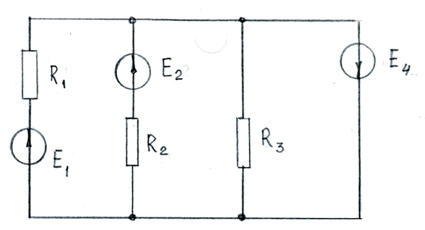
Задача 1.10.
Применяя метод двух узлов для указанной схемы, где
Е1 = 200 В, Е2 = 100 В, Е4 = 90 В, R1 = 20 Ом, R2 = 10 Ом, R3 = 30 Ом,
R4 = 15 Ом, определить токи в ветвях.
2. НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА
Нелинейными называют цепи, в которых сопротивление резистивных элементов не постоянны и зависят от напряжения и тока. Если для линейной цепи постоянного тока задается величина сопротивления резистивного элемента, то для нелинейной цепи задается вольтамперная характеристика нелинейного элемента (ВАХ НЭ) (рис. 2.1. кривая 1)
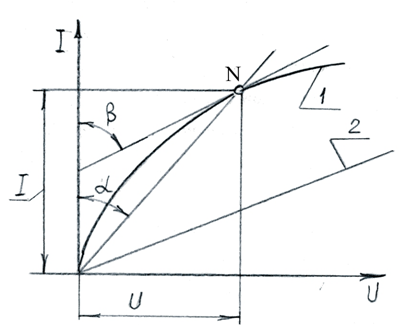
Рис 2.1
Для сравнения на рис 2.1построена прямая 2 – ВАХ линейного элемента.
Каждой точке ВАХ НЭ соответствует определенное сопротивление
R = U/I = (mu/mi)tgα, которое пропорционально тангенсу угла наклона прямой ON, проведенный из начала координат к точке; в которой хотим определить сопротивление, к оси токов (mu – масштаб напряжения, mi – масштаб токов). Это сопротивление называется статическим и представляет собой сопротивление элемента постоянному току.
Кроме статического сопротивления НЭ для каждой точки ВАХ можно определить дифференциальное(динамическое) сопротивление Rдиф, которое равно отношению приращения напряжения ∆U к приращению тока ∆I в данной точке при ∆U и ∆I, стремящихся к нулю.
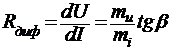 ,
,
т. е. пропорционально тангенсу угла наклона касательной в данной точке характеристики к оси токов. Дифференциальное сопротивление характеризует НЭ при малых изменениях напряжения и тока.
Задача расчета нелинейной цепи постоянного тока состоит в определении токов и напряжений на участках нелинейной цепи при заданных ВАХ, сопротивлениях линейных элементов и ЭДС источников. Задача решается графическим методом.
Возможны соединения элементов последовательное, параллельное и смешенное.
Для закрепления материала предлагается решить задачи:
Задача 2.1.
В схеме с последовательным соединением линейного и нелинейного резисторов с заданными ВАХ и токомI=25мА, определить ЭДС Е источника.
Задача 2.2.
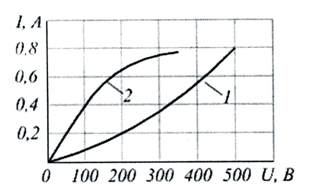
Два нелинейных элемента, ВАХ которых (1и 2) изображены на рисунке, соединены последовательно. Напряжение на первом элементе равно 200 В. Определить напряжение на втором элементе.
Задача 2.3.
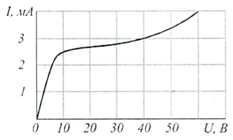
При напряжении U = 10 В определить сопротивление нелинейного элемента с заданной ВАХ
Задача 2.4.
ВАХ U = f(I) нелинейного элемента имеет максимум при токе 5 А и напряжении 350 В. Определить при этом дифференциальное сопротивление.
3. ЭЛЕКТРИЧЕСКИ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
3.1. Получение синусоидальной ЭДС. Основные величины, характеризующие синусоидальные функции времени (напряжение, ЭДС и ток) и основные параметры, однозначно их определяющие (амплитуда, угловая частота, начальная фаза). Величины используемые для характеристики синусоидальных функций времени (период, частота, сдвиг фаз между напряжением и током, действующие значения напряжения, ЭДС и тока).
Для питания электрической цепи переменным током необходимо получить переменную ЭДС.
Простейшим генератором синусоидального тока является проводник в виде прямоугольной рамки, который вращается с постоянной угловой скоростью ω=const в постоянном однородном магнитном поле (рис. 3.1)
Рис. 3.1
В момент начала отсчета (t=0) рамка расположена под углом ψе к плоскости, перпендикулярной линиям магнитного поля.
Согласно закону электромагнитной индукции в каждом продольном проводнике вращающейся рамки будет наводиться изменяющаяся ЭДС e=Blυn, где В – магнитная индукция; l–длина продольного проводника; υn – скорость пересечения магнитных линий, которую можно выразить через ν –линейную скорость движения проводника: 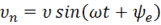 , где ωt – угол поворота рамки за время tотносительно начала отсчета. С учетом последнего, выражение для мгновенного значения ЭДС запишется:
, где ωt – угол поворота рамки за время tотносительно начала отсчета. С учетом последнего, выражение для мгновенного значения ЭДС запишется:
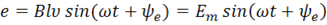 ,
,
где Em=Blν – амплитуда ЭДС.
График изменения ЭДС при вращении рамки показан на рисунке 3.2
Рис. 3.2
В линейных цепях синусоидального тока и ЭДС, и напряжение, и ток являются синусоидальными функциями времени:
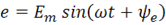 ;
;
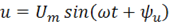 ;
;
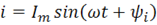 ,
,
где e, u, i – мгновенные значения ЭДС, напряжения и тока соответственно;
ωt+ψe, ωt+ψu, ωt+ψi–фазовые углы ЭДС, напряжения и тока (фазовый угол отсчитывается от точки перехода синусоидальной функции через ноль к положительному значению);
ψe, ψe, ψe – начальные фазы ЭДС, напряжения и тока;
Em, Um, Im – амплитуды (максимальные значения) синусоидальных функций;
Для характеристики синусоидальных функций (кроме указанных) используются следующие величины:
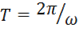 – период (наименьший интервал времени, по истечению которого мгновенные значения периодической величины повторяются);
– период (наименьший интервал времени, по истечению которого мгновенные значения периодической величины повторяются);
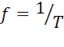 – частота (число периодов в секунду);
– частота (число периодов в секунду);
φ – сдвиг фаз между напряжением и током, φ=ψu-ψi;
E, U, I – действующие значения (среднеквадратичные значения) переменных величин за период:
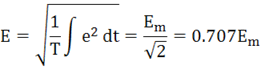
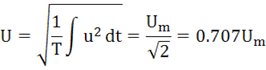
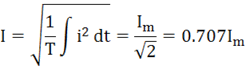
Для закрепления материала решить задачи:
Задача 3.1.
Определить начальную фазу тока, заданного графически на представленном рисунке. Написать уравнение синусоидального тока в численном выражении.
Задача 3.2.
Чему равно действующее значение синусоидального тока
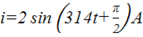 ?
?
Задача 3.3.
Чему равен период Т синусоидального тока, если его частота f=200 Гц?