Нелинейные электрические и магнитные цепи

Задача. К трехпроводной трехфазной сети с линейным напряжением Uл=220 В подключен приемник, фазы которого соединены звездой (Рис.19). Заданы сопротивления Rа=10 Ом, Rв=5 Ом, Xв=8,66 Ом, Хс=10 Ом. Определить токи в ветвях, построить совмещенную топографическую диаграмму напряжений и векторную диаграмму токов.

Решение.

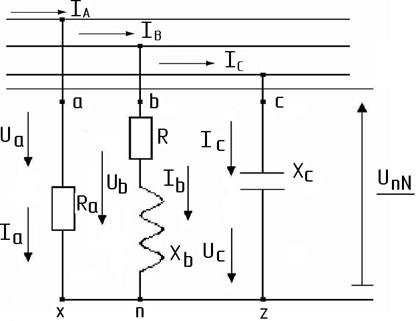
Рис. 19

1)  Фазные напряжения источника образуют симметричную систему

UA=Uфej0=(Uл/)еj0=127еj0 В;

UВ=Uфe-j120°=127 e-j120°= -63,5-j110 В;

UВ=Uфej120°=127 ej120°= -63,5+j110 В.

2)  Комплексные сопротивления фаз приемника: Zа=Rа+jXa= Rа=10 Ом; Zв=Rв+jXв= 5+j8,66=10ej60° Ом; Zс=Rс-jXс= — jXс =-j10=10e-j90° Ом.

Их комплексные проводимости: Yа=1/Zа=1/10=0,1 См; Yв=1/Zв=1/10ej60° =

=0,1e-j60°=0,1(cos60°-jsin60°)=0,1(0,5-j0,866) См; Yс=1/Zс=1/(-j10)=0,1ej90° См.

3)  Смещение нейтрали n относительно N по методу двух узлов

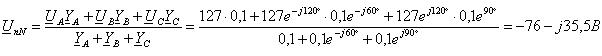
4)  Фазные напряжения приемника из уравнений, составленных по второму закону Кирхгофа для контуров через фазные напряжения источника, приемника и смещения нейтрали:

Ua=UA-UnN=127-(-76-j35,5)=203+j35,5=||=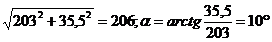

=206ej10° В;

Uв=UВ-UnN=-63,5+j110-(-76-j35,5)=12,5-j74,5=75,5e-j80°30’ В;

Uc=UC-UnN=-63,5+j110-(76-j35,5)=12,5+j145,5=145,6ej85° В;

5)  Фазные токи и токи в линии:

IA=Ia=Ua/Za=206ej10°/10=20,6ej10° A;

IB=Iв=Uв/Zв=75,5e-j80°30’/10ej60° =7,55e-j140°30′ A;

IС=Iс=Uс/Zс=145,6ej85°/10e-j90°=14,5ej175° A;

6) Для построения векторной диаграммы выбираем масштабы напряжения МU=40 В/см и тока МI=5 А/см. Строим симметричную топографическую диаграмму (Рис.20) напряжений генератора и вектор смещения нейтрали UnN=84ej205°=-76-j35,5 В.

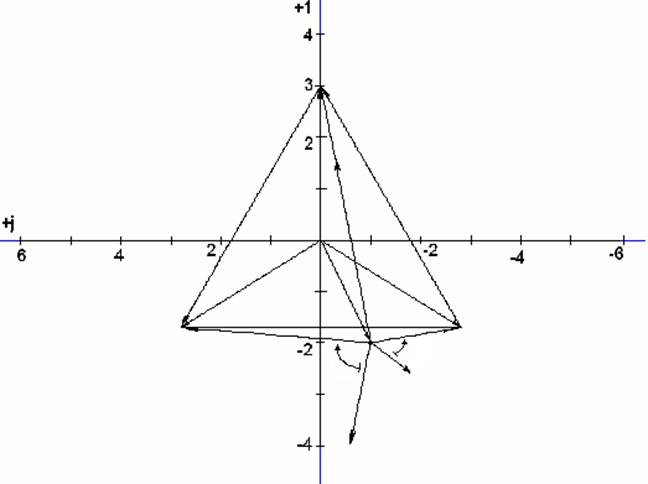
А, а

Ua UAB

UА Ia

N

UCA

UC UnN UB

C, c B, b

Uc φc φb Ub UBC

n

Ib

Ic

Рис. 20

Практическое занятие № 5

Нелинейные электрические и магнитные цепи.

Общие сведения

Нелинейными электрическими и магнитными элементами и цепями называются такие, у которых основные параметры (сопротивление , индуктивность , емкость ) зависят от напряжений, токов, магнитных потоков или других величин.

Различают неуправляемые нелинейные элементы (НЭ) (лампы накаливания, полупроводниковые резисторы, диоды, катушка индуктивности с магнитопроводом и др.), имеющие одну вольт-амперную (вебер-амперную) характеристику (ВАХ) и управляемые (транзисторы, тиристоры), имеющие семейство ВАХ.

1. Нелинейные электрические цепи постоянного тока. Они могут быть с последовательным, параллельном и смешанном включением нелинейных (или линейных и нелинейных) сопротивлений. Нелинейные цепи рассчитываются графическим или аналитическим методами. Графический метод применяется чаще. Этот метод сводится к нахождению ВАХ всей цепи по ВАХ элементов входящих в цепь.

В неразветвленной цепи согласно 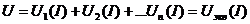суммируются напряжения НЭ при одинаковых токах .

При параллельном соединении общий ток нелинейной цепи 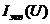равен по первому закону Кирхгофа сумме токов нелинейных элементов при одинаковых напряжениях

В схемах со смешанным включением НЭ расчет проводят с применением правил преобразования схем.

Если линейный элемент соединен с НЭ то рабочую точку находят с помощью второго закона Кирхгофа методом пересечения характеристик (рис. 21 а): 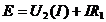на пересечении ВАХ НЭ и прямой определяющей уравнение цепи (рис. 21 б).

Это уравнение цепи является прямой и называется нагрузочной характеристикой. Строится по точкам холостого хода цепи 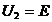и короткого замыкания НЭ ,

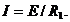
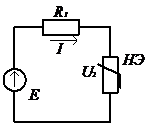
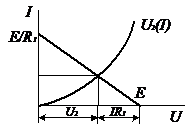
а) б)

Рис. 21

2. Магнитные цепи с постоянной магнитодвижущей силой (МДС).

Постоянный магнит и электрический ток возбуждают магнитное поле. Величина и направление магнитного поля характеризуются его напряженностью . Например, для катушки с током напряженность определяется МДС приходящейся на единицу длины магнитной линии.

Магнитное поле изменяет состояние среды, характеризуемое магнитной индукцией 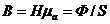, где — абсолютная магнитная проницаемость среды; — магнитный поток; — площадь поперечного сечения; — число витков катушки.

Магнитные цепи рассчитываются по аналогии с электрическими цепями по первому и второму законам Кирхгофа:

— алгебраическая сумма магнитных потоков любого узла магнитной цепи равно нулю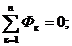

— алгебраическая сумма МДС, действующих в замкнутом контуре, равна алгебраической сумме магнитных напряжений на магнитных сопротивлениях контура (закон полного тока)

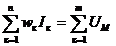, где 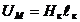— магнитное напряжение;

— длина участка магнитной цепи;

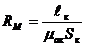— магнитное сопротивление магнитной цепи.