Определение показателя преломления с помощью явления

Таким образом, углы дифракции, под которыми наблюдаются максимумы, определяются условием

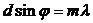. (7)

Здесь m = 0, ±1, ±2,… — порядок дифракционного максимума.

Описание установки

Оптическая схема установки представлена на рис. 5. Излучение лазера 1, проходит через диафрагму, роль которой играет колпачок – насадка на излучателе, и падает на объект 2 (щель, круглое отверстие или дифракционная решетка, которые в данной работе могут быть как вмонтированы в колпачок излучателя, так и предложены отдельно). Дифрагированный свет наблюдается на экране 3. Поскольку в работе используется когерентное излучение лазера, дифракционную картину можно наблюдать на экране без помощи линзы. Но в этом случае лучи, приходящие в одну точку экрана от разных зон, попадают туда под разными углами. Однако, если расположить экран на расстоянии много большем размеров области взаимодействия светового пучка с объектом

(удлинить путь луча позволяют поворотные зеркала 4), то можно считать, что все лучи приходят в заданную точку под одним и тем же углом j. Из рис. 6 видно, что

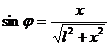(8)

Измерив расстояние от объекта до экрана l и расстояние x от точки, соответствующей нулевому порядку дифракции (главному максимуму), до точки, соответствующей m-му порядку (рис. 6), можно определить размеры объектов по формулам (1), (4), (7), (8).

Итак, согласно вышесказанному, по расположению максисумов и длине волны можно определить размеры препятствий. А по отношению интенсивностей различных максимумов можно найти форму препятствий, например, форму штрихов решетки и различить пиловидную, прямолинейную и различные другие формы, даже не глядя на решетку. Этот принцип служит для определения положения атомов в кристалле, однако, из-за малых размеров препятствий необходимо применять излучение с очень малыми длинами волн, например, рентгеновские лучи.

Порядок выполнения работы

Упражнение 1. Изучение дифракции на щели.

1.  Установить экран таким образом, чтобы лазерный пучок попадал на горизонтальную линию экрана.

2.  С помощью поворотных зеркал получить на экране изображение дифракционных максимумов, расположить их симметрично относительно центра экрана.

3.  Используя миллиметровую сетку, нанесенную на экране, измерить расстояние от середины нулевого максимума до минимума (рис. 6). Измерения провести для нескольких m. Результаты измерений занести в таблицу.

4.  По формулам (1) и (8) найти ширину щели h для каждого xm.

5.  Вычислить среднее значение h.

6.  Оценить погрешность измерений.

Упражнение 2. Изучение дифракции на круглом отверстии.

1.  См. пункт 1 упражнения 1.

2.  С помощью поворотных зеркал получить на экране изображение дифракционных колец, расположить их симметрично относительно центра экрана.

3.  Измерить расстояние xm от нулевого до m-го максимума, используя миллиметровую сетку, нанесенную на экран. Измерения провести для нескольких m. Результаты измерений занести в таблицу.

4.  По формулам (4) и (8) найти диаметр отверстия а для каждого xm.

5.  Вычислить среднее значение диаметра отверстия .

6.  Оценить погрешность измерений.

Упражнение 3. Определение периода дифракционной решетки.

1.  См. пункт 1 упражнения 1.

2.  Получить на экране изображение дифракционных максимумов, (в случае использования дифракционных решеток с малым периодом, возможно, придется отказаться от системы зеркал и располагать экран непосредственно за решеткой).

3.  Измерить расстояние xm от нулевого до m-го максимума, используя миллиметровую сетку, нанесенную на экран. Измерения провести для нескольких m. Результаты измерений занести в таблицу.

4.  По формулам (7) и (8) вычислить период дифракционной решетки d для каждого xm..

5.  Вычислить среднее значение периода решетки .

6.  Оценить погрешность измерений.

Контрольные вопросы.

1.  Что называется дифракцией света?

2.  Основные виды дифракции. Какой из них изучается в данной работе?

3.  Сформулируйте принцип Гюйгенса – Френеля.

4.  Сформулируйте условие максимума для дифракции на длинной и узкой щели.

5.  Как измерить диаметр отверстия с помощью явления дифракции?

6.  Как влияет диаметр отверстия на размеры дифракционной картины?

7.  Как измерить ширину щели с помощью явления дифракции?

8.  Что такое дифракционная решетка?

9.  Что называется периодом дифракционной решетки?

10.  Сформулируйте условие максимумов для дифракционной решетки.

ЛАБОРАТОРНАЯ РАБОТА 4

Определение показателя преломления с помощью явления

поляризации света

Цель работы: знакомство с явлением поляризации света, изучение явлений, связанных с поляризованным светом, знакомство с явлением полного внутреннего отражения света, определение значения показателя преломления стекла.

Оборудование: лазер, два поляризационных фильтра (свет, испускаемый лазером, является частично поляризованным, поэтому выполнить работу можно и без использования поляризационных фильтров), стеклянная призма на вращающемся столике с угловой шкалой, экран.

Описание метода измерения.

Показатель преломления вещества является важным параметром в качественных обсуждениях того, как вещество воздействует на свет. Он является одним из нескольких констант вещества, которую можно определить при помощи обычного света. Луч света, падающий на поверхность, может отражаться в соответствии с законом отражения. Однако отраженный луч редко имеет точно такое же распределение колебаний волны, что и падающий. Это различие называется поляризацией, которое проявляется в изменении интенсивности света, зависящей от угла падения света и природы вещества. Поляризация присуща всему электромагнитному излучению. В этой работе исследуется поляризация видимого излучения.

Световая волна представляет собой процесс распространения в пространстве переменного электромагнитного поля. В любой момент времени в каждой точке пространства векторы напряженности электрического и магнитного полей взаимно перпендикулярны. Поляризованным называется свет, в котором колебания этих векторов упорядочены каким – либо образом. Вектор скорости распространения световой волны ортогонален плоскости, в которой лежат векторы Е и Н, так что эти три вектора образуют правую тройку. Плоскость поляризации можно определить как плоскость, содержащую вектор Е и вектор направления распространения волны .