Основые теории колебаний
Введение
Под колебаниями понимаются повторяющиеся ограниченные движения относительно некоего среднего состояния, которое, в частном случае, может быть положением равновесия. Математическим выражением колебательного движения является периодическая функция, описывающая данный процесс. Общий вид периодической функции:
![]()
Это соотношение справедливо для любого момента времени t, где Т – период функции; 1/T = n – частота; используется также круговая частота w = 2pn. Особое значение имеет простейший вид колебательного процесса — гармоническое колебание:
![]() ;
;
здесь А — амплитуда колебания, wt + j — мгновенная фаза.
Строго периодичный процесс на практике не встречается, но мы можем иметь дело с почти периодичным процессом, удовлетворяющим следующему условию:
![]() ,
,
причём оно выполняется для любого наперёд заданного малого e > 0, а T(e) — почти период. Примером такого процесса может служить процесс затухающих колебаний
![]() ,
,
при l << w. Здесь T(e) = 2p/w — почти период.
Важнейшим свойством колебаний является их изоморфизм, т. е. разные физические процессы описываются одними математическими уравнениями. Для описания колебаний используют различные координаты, однако, физические (первичные) не всегда удобны. Тогда выбирают обобщённые координаты, как некоторую комбинацию первичных координат, такие, что по известному закону преобразования координат решение переводится в первичные координаты.
Тема 1. Колебательные системы
Для изучения реальных колебательных систем необходимо построить модель системы, в которой отражается только ограниченное число основных черт, существенных для изучаемых колебательных процессов.
1.1. Классификация колебательных систем
Заменяя реальные динамические системы их соответственно выбранными моделями, мы можем провести последовательную классификацию систем и протекающих в них колебательных процессов по различным признакам.
1. По свойствам параметров системы, т. е. по отношению к признаку суперпозиции, выделяют системы с параметрами, не зависящими от её состояния (линейные системы), и с параметрами, зависящими от состояния системы (нелинейные системы). Для линейных систем изменение величины внешнего воздействия вызывает количественное изменение отклика пропорциональное внешнему воздействию. Результат совокупного воздействия нескольких сил равен сумме реакций воздействия этих сил по отдельности. Для нелинейных систем изменение величины внешнего воздействия может привести к качественному изменению реакции системы.
2. По числу степеней свободы системы бывают дискретные и сплошные. Дискретные системы — это системы, колебательный процесс в которых описывается обыкновенными ДУ; в сплошных системах процесс описывается ДУ в частных производных. Параметром дискретных систем является порядок ДУ (или, что то же самое, число степеней свободы); в сплошных — число измерений.
3. По энергетическим признакам системы делятся на консервативные (энергия сохраняется) и неконсервативные (энергия изменяется). В свою очередь неконсервативные системы делятся на пассивные (которые не содержат источников внутренней энергии) и активные (включают источники внутренней энергии).
4. По условиям действия системы разделяют на автономные (не испытывают внешнего воздействия) и неавтономные (находятся под внешним воздействием). Неавтономные также делятся по способу воздействия. Если непосредственно внешняя сила воздействует на обобщённые координаты, то это силовое воздействие; если внешним воздействием меняется параметр колебательной системы, то такое воздействие называется параметрическим; если меняются и координаты, и параметр, то воздействие смешанное или комбинационное. Нужно отметить, что внешнее воздействие может быть медленным (по сравнению с периодом), малым (по сравнению с амплитудой), случайным, периодическим.
1.2. Уравнения линейных дискретных колебательных систем Вопрос 1
Общим подходом к моделированию колебательных систем, в котором определены кинетическая и потенциальная энергии является формализм Лагранжа. В радиотехнических системах, которые можно представить соединением конечного числа элементов (активных и пассивных), оказывается полезным метод уравнений Кирхгофа (основан на том, что токам и напряжениям ставится в соответствие их изображения по Лапласу):
|
|
(1.1) |
Свойства преобразования Лапласа:
|
1. Линейность: |
(1.2) |
|
2. Правило сдвига: |
(1.3) |
|
3. Дифференцирование: |
(1.4) |
|
4. Интегрирование: |
(1.5) |
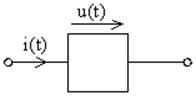
Для линейных двухполюсников, общий вид которых представлен на рис.1, вводят понятия операторного сопротивления и операторной проводимости:
![]() и
и ![]() ,
,
где I(p) и U(p) — изображения по Лапласу тока и напряжения соответственно, т. е.
![]() ,
, ![]() .
.
Определим теперь операторные сопротивления Z и проводимости Y для типовых идеальных двухполюсников, пользуясь свойствами (1.2), (1.4) и (1.5).
|
Рис. 1. Двухполюсник. |
Для резистора: Ri(t) = u(t) Û U(p) = RI(p), тогда Z = R, Y = 1/R. Для конденсатора: Для индуктивности: |
Запишем также законы Кирхгофа в операторной форме:
|
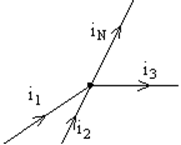
1. Сумма токов, сходящихся в узле, равна нулю, т. е. |
Рис. 2. Иллюстрация к первому правилу Кирхгофа: узел. |
|
|
(1.6) |
|
2. Сумма напряжений на всех элементах произвольного замкнутого контура равна нулю (в операторной форме): |
|
|
|
(1.7) |
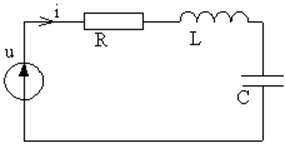
Рассмотрим последовательный и параллельный колебательные контура (см. рис. 3, рис. 4). Можно записать следующие уравнения (для последовательного колебательного контура), которые следуют из закона Ома:
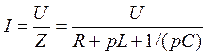
или (если избавиться от p в знаменателе)
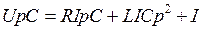 .
.
Теперь, применяя свойства преобразования Лапласа, запишем последнее уравнение в виде
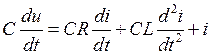 .
.
|
Рис. 3. Последовательный колебательный контур. |
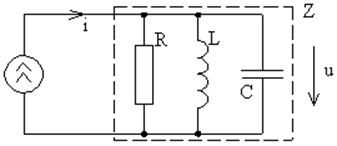
Рис. 4. Параллельный колебательный контур. |
Для параллельного колебательного контура проделаем аналогичные процедуры: из закона Ома, а также правила сложения сопротивлений при параллельном соединении следует, что
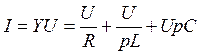 .
.
Приведя к общему знаменателю, получим: 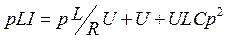 . Перейдём теперь от уравнения в операторном виде к дифференциальному уравнению:
. Перейдём теперь от уравнения в операторном виде к дифференциальному уравнению:
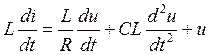
Таким образом, можно получить некоторые операторы:
|
|
(1.8) |
Эти операторы, в общем случае, интегрально-дифференциальные, но это не очень удобно, поэтому мы и приводили уравнения к общему знаменателю и получали при этом уравнения вида
|
|
(1.9) |
где ![]() и
и ![]() — линейные дифференциальные операторы, т. е.
— линейные дифференциальные операторы, т. е.
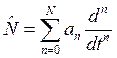 и
и 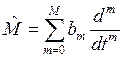 .
.
Применим преобразование Лапласа к (1.9) с учётом свойств (1.2) и (1.4):
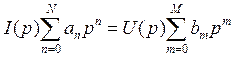 .
.
Формально можно найти операторное сопротивление системы:
|
|
(1.10) |
т. е. операторное сопротивление есть дробно-рациональная функция.
Пусть теперь на линейную систему производится гармоническое воздействие u(t) = Ucos(wt + j). Будем считать, что параметры системы (an и bm) постоянны, т. е. у нас есть система с постоянными параметрами. Из свойств линейных систем с постоянными параметрами вида (1.9) следует, что в установившемся режиме реакция системы на гармонический сигнал будет гармоническим сигналом той же частоты, т. е. i(t) = Icos(wt + y). Воспользуемся методом комплексных амплитуд: поставим во взаимооднозначное соответствие сигналам их комплексные амплитуды, тогда
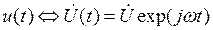 , где
, где 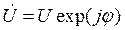 ;
;
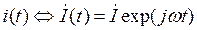 , где
, где 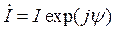 .
.
Для линейных операторов выполняется соотношение:
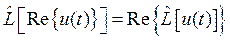 ,
,
с помощью которого можно записать (1.9) в виде:
![]() ,
,
и тогда найдём комплексное сопротивление как отношение комплексных амплитуд:
|
|
(1.11) |
Таким образом, мы нашли сопротивление операторным методом и методом комплексных амплитуд. Операторный метод предполагает, что сигнал начался в момент времени t = 0. Он справедлив как в установившемся, так и в переходном режиме. В методе комплексных амплитуд предполагается, что сигнал начался давно (установившийся режим).
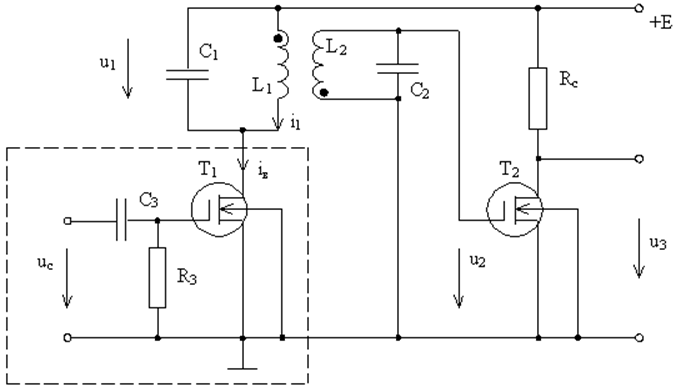
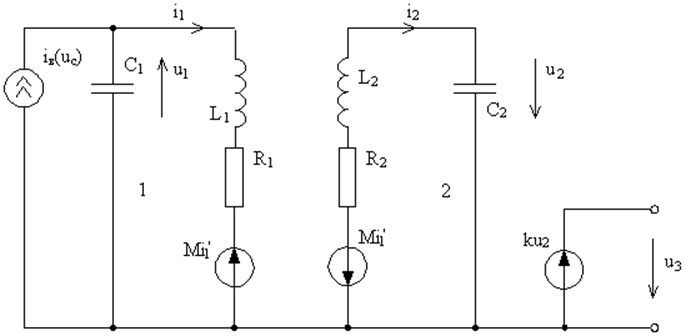
Рассмотрим для примера составление уравнения для резонансного усилителя (см. рис. 5). Полевой транзистор представляет собой источник тока, и приложенное напряжение заставляет его генерировать ток. Таким образом, часть резонансного усилителя, которая на рис. 5 обведена штриховой линией, можно принять за источник тока и перерисовать усилитель в эквивалентном виде, который представлен на рис. 6. Резисторы R1 и R2 описывают потери в резонансных контурах L1C1 и L2C2. Второй каскад на транзисторе T2 усиливает напряжение в k раз, т. е. u3 = ku2.
Выберем в качестве обобщённых координат токи i1 и i2. Запишем второе правило Кирхгофа для первого и второго контуров на рис. 6.
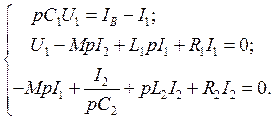
Умножим второе уравнение на pC1, а третье на pC2:
|
Рис. 5. Резонансный усилитель. |
|
Рис. 6. Эквивалентная схема резонансного усилителя. |
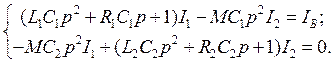
Из этой системы по правилу Крамера найдём I2, а затем по закону Ома для участка цепи найдём напряжение на конденсаторе С2:
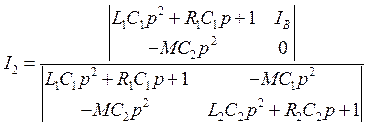 ,
, 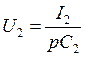
или
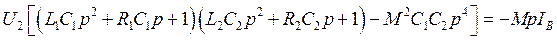 .
.
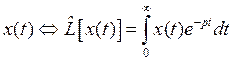
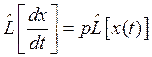 .
.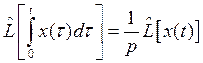 .
.
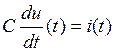 Û I(p) = CpU(p),
Û I(p) = CpU(p), 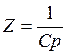 , Y = Cp.
, Y = Cp.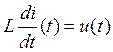 Û U(p) = LpI(p), Z = Lp,
Û U(p) = LpI(p), Z = Lp, 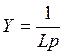 .
.
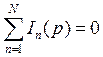
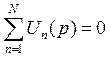
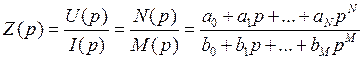 ,
,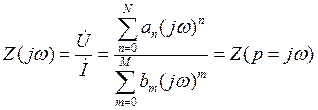 .
.