Параметрические генераторы и усилители
|
|
(5.9) |
Таким образом, частота установившихся колебаний, в принципе, может быть меньше частоты собственных колебаний системы.
Рассмотрим ещё один интересный случай. Итак, мы сказали, что в системе идёт подкачка энергии при параметрическом возбуждении. У нас получается генератор. Обычный генератор преобразует энергию постоянного питания (постоянного напряжения) в энергию гармонических колебаний (переменный ток). Здесь, когда будет превзойдён порог параметрического возбуждения, будет преобразовываться энергия параметрического воздействия. А если есть ещё более сложная система (испытывает и параметрическое и силовое воздействия), то в этом случае, если часть энергии параметрического воздействия перейдёт в усиление вынужденных колебаний, мы получим параметрический усилитель.
5.2. Параметрические генераторы и усилители
Мы сказали, рассматривая простейший колебательный контур (рис. 34), что при определённых условиях (если меняем ёмкость конденсатора вдвое чаще, чем установившийся процесс колебаний и в нужной фазе) идёт подкачка энергии. Мы доказали, что эта подкачка и потери за период пропорциональны квадрату установившейся амплитуды. Потери в системе описываются сопротивлением R (положительным), но если подкачка энергии в системе точно также пропорциональна квадрату амплитуды, как и потери, становится естественно описать параметрическую подкачку в такой системе введением отрицательного сопротивления R –.
Чему должно быть равно это сопротивление? Мы должны его выбрать из тех условий, чтобы эквивалентные отрицательные потери, которые рассматриваем как добавку энергии, равнялись той величине, которую мы посчитали на самом деле. Таким образом, отсюда мы получаем выражение для эквивалентного отрицательного сопротивления, которое вносит в контур параметрическое возбуждение
|
|
(5.10) |
(мы рассматриваем случай первого параметрического резонанса).
Добавление энергии в колебательную систему от источника параметрического воздействия, периодически меняющего энергоёмкий параметр, называется параметрической регенерацией. Естественно, если подкачка энергии в системе превосходит потери в ней, т. е. |R – | > R, то колебания в системе развиваются без внешнего силового воздействия (параметрический генератор). Если |R – | < R, это означает, что параметрическое воздействие не достигло порога параметрического возбуждения (энергия подкачивается, но колебания не возникают). Но, если при этом ещё в контур включить дополнительный источник напряжения, который будет воздействовать на частоте близкой к частоте w0, то возникнут вынужденные колебания. Если они возникнут, то сразу пойдёт подкачка энергии. Она всё равно не будет превосходить потери (т. е. генерации не возникнет), но мы эквивалентно уменьшим потери в системе, т. е. эквивалентно увеличим энергию колебаний. У нас получится параметрический усилитель.
Пусть на вход усилителя воздействует гармонический сигнал на резонансной частоте контура u1 = U1cos(w0t). Тогда для амплитуды тока в контуре получаем
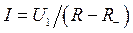 .
.
Тогда падение напряжения на сопротивлении R составит
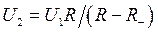 .
.
Таким образом, коэффициент усиления по напряжению равен
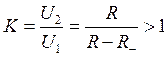 .
.
Коэффициент усиления может быть довольно высоким. Недостаток такого усилителя — узкая полоса Dw » w0/(KQ), где Q = w0L/C0 — добротность контура. По этой причине одноконтурные параметрические генераторы и усилители применяются редко.
|
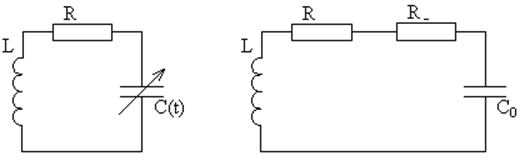
Рис. 34. Колебательный контур с параметрическим воздействием (слева) и эквивалентная схема такого контура (справа). |
Тема 6. Автоколебательные системы с одной степенью свободы
Конструкция, которая генерирует колебания без внешнего воздействия, называется автоколебательной системой. Автоколебательные системы являются автономными (на них нет воздействия), а также активными (генерируют энергию). Колебательный процесс всегда периодический, а это значит, что полная колебательная энергия системы N = T + V (здесь Т — кинетическая энергия) является периодической функцией времени, т. е. N(t + nT) = N(t) (здесь Т — период колебаний). С другой стороны, в системе действует диссипация, тогда из известного уравнения (1.35)
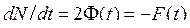 ,
,
где F(t) — функция, характеризующая диссипативные свойства системы, причём для диссипативных систем F(t) > 0. Также для F(t), исходя из предыдущего равенства и периодичности функции N, справедливо
|
|
(6.1) |
Но так как для автономных диссипативных систем функция F(t) всегда положительна (а интеграл от всегда положительной функции не может быть равен нулю), то это значит, что в автономных диссипативных системах устойчивые автоколебания невозможны, т. е. всегда требуется подкачка энергии. Например, если рассмотреть простейший последовательный RLC колебательный контур, то функция диссипации будет F(t) = R(i)i2. Таким образом, чтобы возникли устойчивые колебания, необходимо, чтобы значение R(i) хотя бы на каких-то участках было отрицательным.
6.1. Классификация автоколебательных систем
Любая автоколебательная система состоит из некоторого накопителя колебательной энергии (например, резонансный контур) и системы обратной связи (системы управления), которая обеспечивает подкачку энергии в систему от внешнего источника, так скажем, "в такт". По отношению накопителя к подкачке автоколебательные системы делятся на два широких класса:
1. Осцилляторные системы. В них накопитель энергии является высокодобротным контуром, а добавка энергии от внешнего источника за период колебаний много меньше, чем запас колебательной энергии системы. Это можно объяснить просто. Нам известно, что подкачка должна компенсировать потери. В установившемся режиме подкачка энергии за период в точности равна потерям. Дадим определение добротности: это отношение накопленной энергии к потерям за период. Если добротность велика, то потери за период малы в сравнении с накопленной энергией, следовательно, в осцилляторной системе и подкачка мала в сравнении с накопленной энергией. При этом, если эта подкачка является малым возбуждением, то можно ожидать, что форма колебаний в осцилляторных системах близка к синусоидальной. В этом случае амплитуда и частота колебаний определяются характеристиками системы (характеристиками накопителя) и мало зависит от системы обратной связи.
2. Релаксационные системы. Накопитель является апериодической системой, а обмен энергией накопителя с внешним источником за период колебаний сравним с запасом энергии в накопителе. Форма колебаний далека от синусоиды и сильно зависит от свойств обратной связи (например, RC мультивибратор).
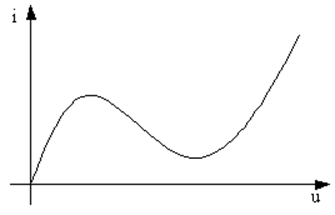
В качестве знакопеременного сопротивления в автоколебательных системах могут использоваться нелинейные двухполюсники. Нелинейность может быть двух видов: N-типа и S-типа (рис. 35, 36) в зависимости от вида ВАХ нелинейного двухполюсника. Причём, как видно из ВАХ, функции двузначные, поэтому двухполюсники N-типа удобно описывать функцией, где в качестве аргумента взято напряжение, т. е. i = j(u); а S-типа описывать функцией, аргументом в которой будет ток, т. е. u = y(i).
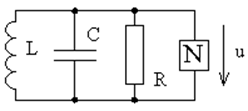
В случае параллельного подсоединения нелинейного двухполюсника с отрицательным дифференциальным сопротивлением к параллельному контуру необходимо использовать элемент с характеристикой N-типа, показанной на рис. 35, так как общим для всех элементов такой колебательной системы является напряжение u.
|
Рис. 35. ВАХ нелинейного двухполюсника N-типа. |
Рис. 36. ВАХ нелинейного двухполюсника S-типа. |
Уравнение Кирхгофа для этой системы (рис. 37) имеет вид
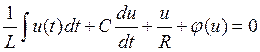
или после дифференцирования
|
|
(6.2) |
где j’(u) = di/du — дифференциальная проводимость нелинейного элемента с падающей характеристикой, называемая также крутизной характеристики. Исследуем систему, которая описывается уравнением (6.2), на устойчивость. Для этого рассмотрим состояние равновесия u0. Мы приложили малую амплитуду колебаний, и смотрим, будут ли они нарастать, или будут оставаться постоянными. В этой ситуации при очень малых амплитудах колебаний мы можем положить, что j’(u) » const. Характеристическое уравнение будет иметь вид
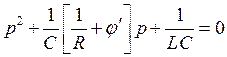 ,
,
решение которого
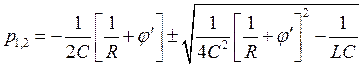 .
.
Так как решение уравнения (6.2) имеет вид
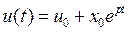 ,
,
то отсюда видно, что условие нарастания амплитуды колебаний следующее Re(p1,2) > 0. Для этого нужно, чтобы, во-первых, j’(u0) < 0 и, во-вторых, |j’(u)| > 1/R.
|
Рис. 37. Схема колебательной системы с нелинейным активным элементом с характеристикой N-типа. |
Рис. 38. Схема колебательной системы с нелинейным активным элементом с характеристикой S-типа. |
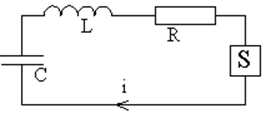
При последовательном соединении элементов (рис. 38) общим для всех элементов является ток i. Из правил Кирхгофа по аналогии, уже продифференцировав и разделив на L, получим уравнение движения в такой системе
|
|
(6.3) |
Проверяя на устойчивость, мы получаем условие неустойчивости колебаний относительно некоторого состояния покоя i0: y’(i0) < 0, |y’(i0)| > R.
Видно, что для обоих случаев первичные координаты разные (в (6.2) это напряжение u0, в (6.3) это ток i0), но на самом деле структура уравнений одна и та же, что в лишний раз подчёркивает изоморфизм процесса. Таким образом, уравнения (6.2) и (6.3) могут быть записаны в безразмерных обобщённых координатах и с безразмерным временем t = wt, где w2 = 1/(LC) в одинаковой форме
|
|
(6.4) |
Если функция ![]() , то это консервативная система (линейный осциллятор); если
, то это консервативная система (линейный осциллятор); если 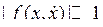 , то система близка к консервативной (здесь функция в общем случае описывает и нелинейность и диссипацию). Соответственно, если система близка к линейной, т. е. имеет малую нелинейность и малую диссипацию, то она называется томпсоновской (автоколебательная система с одной степенью свободы и малыми нелинейностью и диссипацией). Малость диссипации определяется по сравнению с запасённой энергией, т. е. томпсоновская система — это частный случай осцилляторной системы.
, то система близка к консервативной (здесь функция в общем случае описывает и нелинейность и диссипацию). Соответственно, если система близка к линейной, т. е. имеет малую нелинейность и малую диссипацию, то она называется томпсоновской (автоколебательная система с одной степенью свободы и малыми нелинейностью и диссипацией). Малость диссипации определяется по сравнению с запасённой энергией, т. е. томпсоновская система — это частный случай осцилляторной системы.
Если, как обычно, положить ![]() , то уравнение фазовых траекторий для системы (6.4):
, то уравнение фазовых траекторий для системы (6.4):
|
|
(6.5) |
Из физических определений известно, что если система является автоколебательной, то в ней должен существовать стационарный колебательный процесс, который на фазовой плоскости соответствует замкнутой фазовой траектории. Если автоколебания в системе устойчивы, то и замкнутая фазовая траектория также должна быть устойчива, т. е. к ней должны сходиться все фазовые траектории в близкой её окрестности. Подобные предельные фазовые траектории называют предельными циклами.
Уравнение энергетического баланса (6.1) на предельном цикле будет иметь вид
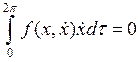 .
.
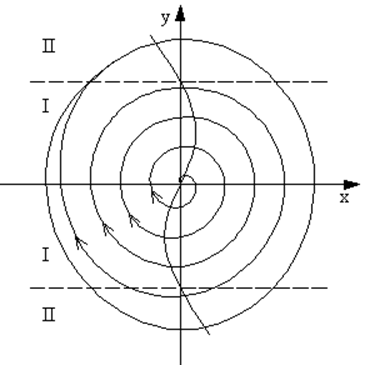
Рассмотрим простейший случай, когда диссипация определяется только скоростью: f(x, y) = f(y). Пусть существует какая-то точка равновесия x = x0, y = 0 (система, приведённая в точку равновесия с нулевой скоростью, в ней остаётся навсегда). В этой точке f(0) = 0. Вблизи равновесия функция f зависит только от y, тогда можно ожидать, что вблизи этой точки f(y) » f ‘(0)y. Для неустойчивости состояния покоя необходимо, чтобы f ‘(0)y < 0. В этом случае в системе происходит увеличение колебательной энергии. График —f(y) для автоколебательной системы с малыми потерями должен иметь вид, показанный на фазовой плоскости рис. 39.
|
Рис. 39.Фазовые траектории для томпсоновской системы. |
При малых f(y) фазовые траектории напоминают окружности, а колебания в системе близки к гармоническим. Подобные автоколебательные системы принадлежат к системам томпсоновского типа. Следовательно, для томпсоновских автоколебательных систем характерна малость f(y) (|f(y)| << 1), что физически означает малую убыль и малое пополнение энергии за период колебаний в стационарном режиме. Начало координат является неустойчивой особой точкой типа фокус, и все траектории, выходящие из начала координат, через большее или меньшее число периодов колебаний (в зависимости от добротности накопительного элемента системы) приходит на предельный цикл. |
В зависимости от знака f(y) вся фазовая плоскость делится на следующие области: I — инкрементная область, в которой вложение колебательной энергии превосходит потери; II — декрементные области, в которых потери превосходят вложения энергии (см. рис. 39).
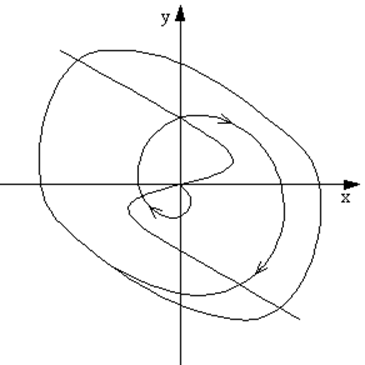
Для автоколебательной системы, для которой функцию f(y) нельзя считать малой (|f(y)| ~ 1), фазовый портрет системы имеет вид, показанный на рис. 40. В такой системе колебания заметно отличаются от гармонических, процесс установления стационарных автоколебаний происходит значительно быстрее, чем в случае, показанном на рис. 39. Энергообмен в системе значительно больше, чем в системах томпсоновского типа, и выход на предельный цикл происходит примерно за период колебаний. Автоколебательная система такого типа занимает промежуточное положение между системами томпсоновского и релаксационного типов (она всё ещё осцилляторная, но уже не томпсоновская).
|
Рефераты по физике сдают здесь
Другие статьиПохожая информацияУзнать стоимость за 15 минут
Распродажа дипломных
Подпишись на наш паблик в ВК
Нужна работа?
|
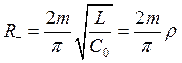
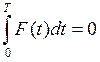 .
.

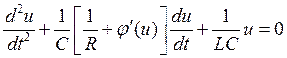 ,
,
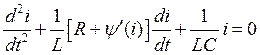 .
. .
.