ВУЗы по физике
Готовые работы по физике
Как писать работы по физике
Примеры решения задач по физике
Решить задачу по физике онлайнПервая пара уравнений максвелла в интегральной форме
Здесь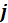 
– омическая плотность тока, связанная с движением зарядов в проводниках; 
— плотность тока смещения, определяемая выражением:
Величина введена для обеспечения непрерывности электрического тока в цепях. Например, если в цепи есть конденсатор. По цепи бежит ток, а между обкладками конденсатора будет течь ток смещения.
Продифференцируем вторую пару еще раз по µ. Т. к.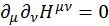 
, получаем уравнение непрерывности плотности тока:
Можно записать это выражение в явном виде. Для этого просуммируем это выражение по µ:
Отсюда получаем уравнение непрерывности плотности тока в явном виде:
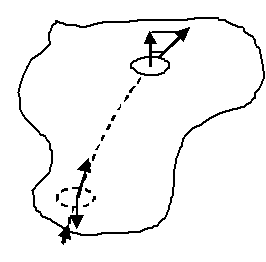
В теории поля под плотностью тока понимают плотность потока электрической жидкости (электрически заряженной), если считать ее несжимаемой, т. е.
С учетом выражения (3.4.19), и определяя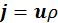 
из (3.4.6), для уравнения непрерывности получим:
Следовательно,
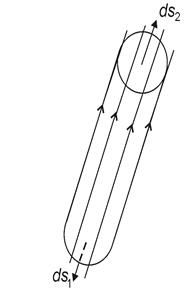
Рассмотрим случай трубки с током (см. рис.).
|
|
Выберем замкнутую поверхность в виде трубки с током так, чтобы боковая поверхность была ограничена линиями тока, а сечения задавались бы векторами нормалями
Если считать, что в единицу времени через единицу площади поперечного сечения трубки тока всегда проходит одно и то же количество жидкости, то |
.
и 
. Вектор 
. Поэтому
В итоге получаем, что
Получили, что внутри объема заряд все время остается постоянным.
§ 3.5. Первая пара уравнений Максвелла в интегральной форме
Уравнения Максвелла в интегральной форме очень удобны при рассмотрении граничных условий и геометрии электромагнитных полей.
Рассмотрим первую пару уравнений в дифференциальной форме.
Для того чтобы получить уравнение в интегральной форме, надо проинтегрировать (3.5.1) по всему пространству:
|
Используя теорему Гаусса-Остроградского, заменяем интегрирование по объему на интегрирование по замкнутой поверхности, которая ограничивает данный объем.
где вектор Скалярное произведение |
. Этот вектор направлен по внешней нормали (см. рис.).
является элементарным потоком Тогда полный поток напряженности магнитного поля через замкнутую поверхность равен нулю, т. е.:
Рассмотри магнитный поток подробнее.
где α – угол между направлениями 
и 
, а 
– проекция на нормаль . Поток может быть как отрицательным, так и положительным. Для выходящих линий магнитного поля α– острый, следовательно,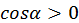 
, и поток 
положителен. Если же линии входящие, то α – тупой угол и поток будет отрицательным. Полный поток линий напряженности магнитного поля состоит из суммы потока входящих линий напряженности и потока выходящих линий, а полный поток, как мы уже знаем, равен нулю:
МГМИМО