Понятие о резонансе напряжений

Общий ток в цепи равен векторной сумме токов.

Для определения угла сдвига фаз между током и напряжением каждой вет­ви вычисляют:

По таблице тригонометрических функций находят, что если cos 1=0,157, то угол сдвига фаз в первой ветви 1=80055’; если cos 2=0,305, то угол сдвига фаз 2=72015’; если cos 3=0,79, то угол сдвига фаз 3=37050’;

Зная угол сдвига фаз между током и напряжением для каждой ветви, построим векторную диаграмму токов и напряжения и определим по ней общую силу тока в цепи.

Для этого отложим  по горизонтали  в выбранном  масштабе  вектор  напряжения U.

Под  углом  1=80°66′  с помощью  транспортира  отложим  вектор  тока I1=7,85 а. Под углом 2=72°15′ (к горизонтали)  отложим  вектор  I2= 10,15 а как продолжение вектора  I1. Под углом 3=37°50′ (к Горизонтали) отложим вектор I3= 19,7 а как продолжение  вектора I2. Общий  ток равен  длине вектора I с учетом  выбранного  масштаба, который соединяет  начало  вектора I1 и конец  вектора I3. Для нашего примера он равен 36,5 а. Общий угол сдвига фаз между током I и напряжением U измеряют с помощью транспортира, он равен 56°.

§ 58. ПОНЯТИЕ О РЕЗОНАНСЕ НАПРЯЖЕНИЙ

В цепи переменного тока с активным, индуктивным и емкостными сопротивлениями, соединенными последовательно  (рис. 59, а), может возникнуть резонанс напряжений.

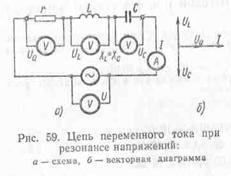
При резонансе напряжения на зажимах индуктивного и емкостного сопротивлений могут стать значительно больше  чем напряжение на зажимах цепи.

Резонанс  напряжений  наступает в том случае, если ин­дуктивное  сопротивление ХL и емкостное  сопротивление  ХC равны между собой, т. е.

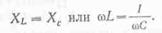
Допустим,  что  подбором  индуктивности  и  емкости  или  изменением частоты создано условие, при котором ХL=ХС. Когда цепь не настроена в резонанс, то ее полное сопротивление

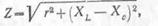
а в рассматриваемой цепи при резонансе (когда ХL=ХC) ее полное; сопротивление

Таким образом, полное сопротивление цепи при резонансе оказывается равным активному сопротивлению.

Уменьшение полного сопротивления цепи приводит к тому, что сила тока в ней возрастает. Напряжение генератора переменного  тока, включенного в цепь, расходуется на активном сопротивлении

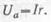
Напряжение на индуктивности определяется согласно закону Ома произведением силы тока на величину индуктивного сопротивления  Так как в цепи увеличилась  сила  тока,  то  напряжение

UL=IXL возросло.

Напряжение на емкости также определяется произведением тока на величину емкостного  сопротивления.  Поэтому  напряжение на емкости Uс=IХс.

В связи с тем, что в последовательно соединенных сопротивле­ниях протекает одинаковый ток и при резонансе индуктивное сопро­тивление ХL равно емкостному сопротивлению Хс, напряжение на индуктивности и напряжение на емкости равны:

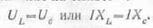
Если одновременно увеличить оба реактивных сопротивления ХL и Хс, не нарушая при этом условия резонанса ХL=Хс, то соответ­ственно возрастут оба частичных напряжения UL и Uс, а сила тока в цепи при этом не изменится. Таким путем можно получить UL и Uс во много раз большие, чем напряжение U на зажимах цепи.

Построим векторную диаграмму (рис. 59, б) для рассматривае­мой цепи при резонансе напряжения. Отложим по горизонтали в выбранном масштабе вектор тока I. В активном сопротивлении ток

и напряжение совпадают по фазе. Поэтому вектор напряжения Uа отложим по вектору тока. Так как напряжение на индуктивности опережает ток на 90°, то вектор UL, отложим вверх под углом 90°.

Напряжение  на  емкости  отстает от тока на 90°, поэтому вектор Uс, равный вектору UL, отложим вниз под углом 90° к вектору тока. На векторной диаграмме видно, что напряжение на индуктив­ности и напряжение на емкости равны и сдвинуты по фазе друг от­носительно друга на 180° и взаимно компенсируются.

Угол сдвига фаз между током и напряжением при резонансе ра­вен нулю. Это значит, что ток и напряжение совпадают по фазе (как в цепи с активным сопротивлением).

Пример. В цепь переменного тока включены последовательно активное со­противление r = 5 ом, индуктивность L = 0,005 гн и емкость 63,5 мкф. Генератор, включенный в цепь, вырабатывает переменное напряжение U=2,5 в с резонанс­ной частотой f=285 гц. Определить индуктивное и емкостное сопротивления, пол­ное сопротивление цепи, ток, протекающий в цепи, напряжение на емкости и на индуктивности.

Решение. Индуктивное сопротивление

Емкостное сопротивление

Индуктивное сопротивление равно емкостному сопротивлению и, следовательно, в цепи наступает резонанс напряжения.

Полное сопротивление цепи при резонансе

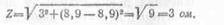
Сила тока в цепи

Напряжение на индуктивности

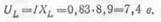
Напряжение на емкости

Как видно из приведенного примера, напряжения на индуктивности  и емкости равны и превышают напряжение генератора.

§ 59. ПОНЯТИЕ О РЕЗОНАНСЕ ТОКОВ

В цепи переменного тока, в которой индуктивность  и  емкость соединены параллельно (рис. 60,а), может возникнуть резонанс токов при условии равенства токов в индуктивности IL„ и емкости IC.

В результате резонанса токов общий ток в цепи может быть от­носительно мал, а в контуре

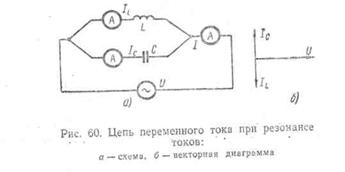
индуктивности и емкости, где происходят электрические колебания, протекает переменный ток, значитель­но больший общего.

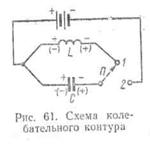
Для понимания сущности резонанса токов выясним, как получаются электрические колебания в цепи, состоящей из параллельно соединенных  индуктивности и емкости.

Для этого рассмотрим схему (рис. 61). Если установить переключатель П в положение 2, то конденсатор заряжается до напряжения источника электрической энёргии.  Перемещением переключателя в положение 1 конденсатор отключается от источника  электрической энергии и оказывается присоединенным к катушке индуктивности. Конденсатор разряжается, и по катушке протекает ток разряда, в результате этого появляется магнитное поле, которое пересекаете «собственные» витки катушки, и в ней возникает э. д. с. самоиндукции, препятствующая увеличению тока.

Ток  будет возрастать постепенно и достигнет наибольшей величины в тот  момент, когда конденсатор разрядится. К этому времени энергия  электрического поля конденсатора превращается в энергию магнитного поля катушки индуктивности.