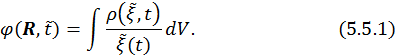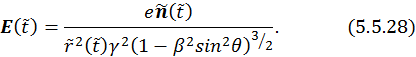Потенциалы и поля произвольно движущегося заряда

А т. к. лапласиан не содержит и , то (5.4.9) примет вид:

где 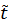– время фиксации поля в точке наблюдения. Сделаем замену переменных:

Подставим (5.4.12) в (5.4.11), получим:

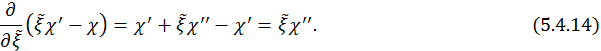
Т. к. , ее можно вынести, и от (5.4.15) останется только:

Это уравнение для плоских электромагнитных волн, распространяющихся вдоль (хотя, в целом, волна сферическая). Решение этого уравнения выглядит следующим образом:

где 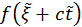– волна, идущая к заряду из бесконечности, а 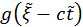– от заряда к бесконечности. Причем, эти два слагаемых имеет смысл: поля на бесконечности спадают. Из бесконечности к заряду ничего не приходит, следовательно,

Это решение (5.4.18) удовлетворяет условию причинности, т. е. поле придет в точку с течением времени, когда 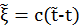. Т. к., это решение является запаздывающим во времени (начало вектора взято в момент времени 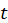, а конец – в 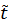). Запаздывающий потенциал в этом случае равен:

2. Найдем решение нашего неоднородного уравнения вблизи от заряда, т. е. при . Отбросить правую часть уравнения (5.4.7) уже нельзя, но в этом случае существенно изменяется левая часть. Временная производная в волновом уравнении значительно уступает по величине координатной производной.

Т. к.

то в (5.4.7) остаются члены:

Решением этого уравнения является потенциал

Чтобы найти все поле, нужно применить принцип суперпозиции полей.

Результирующий потенциал запишется в виде:

где роль играет элемент объема клеточки с зарядом . Таким образом, (5.4.26) – полный запаздывающий скалярный потенциал. Обобщая на случай векторного потенциала, имеем:

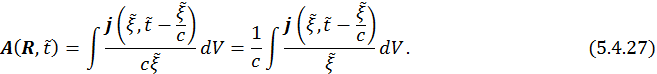
Здесь является немой переменной, т. к. при интегрировании она уйдет, и останутся только те переменные, которые характеризуют поле движущегося заряда.

Четырехмерный векторный потенциал будет равен:

Это выражение характерно тем, что в левой части стоит время 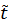— которое соответствует наблюдению, а правой части стоит момент времени t – который соответствует моменту излучения, это траекторное время. Так как 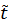более поздний момент времени, то эти потенциалы получили название запаздывающие потенциалы.

Следует заметить, что с математической точки зрения возможно решение, связанное с волной, идущей от наблюдателя к источнику излучения. В этом случае, такое решение будет называться опережающим потенциалом.

С физической же точки зрения такое решение бессмысленно, т. к. поле создается зарядами, потому что нарушается принцип причинности. Таким образом, опережающие потенциалы мы рассматривать не будем. Однако в теоретической физике опережение поля используют для наведения некоторой симметрии в теории поля. Время запаздывания:

§ 5.5. Потенциалы и поля произвольно движущегося заряда

а) Вывод потенциалов на основе запаздывающих потенциалов.

Но – траекторное время (время появления поля). -функция в (5.5.2) не установит соотношения между 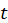и 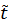. Введем временную -функцию, которая устанавливает связь между 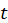и 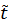. Тогда (5.5.1) можно переписать в виде:

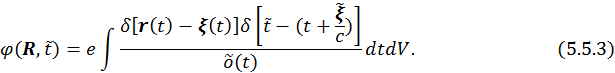
Прежде всего, проинтегрируем (5.5.3) по или по (снимем пространственный интеграл), тогда

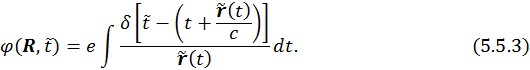
Используем свойство — функции:

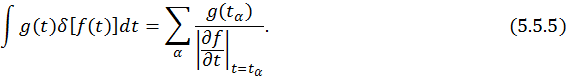
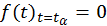Здесь – корень уравнения . Т. к. — функция – четная функция, можно записать:

Запишем в явном виде:

Т. к. не зависит от времени, то

Уравнение 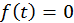имеет в данном случае только один корень 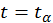(это следует из принципа причинности). При движении атома в сплошной среде может возникнуть два и даже больше корней (излучение Вавилова – Черенкова). В итоге приходим к такому потенциалу:

где .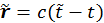

Векторный потенциал согласно (5.4.27) в этом случае равен:

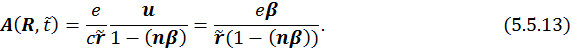
Окончательно, четырехмерный векторный потенциал имеет вид:

Потенциалы называются потенциалами Лиенара – Вихерта.

Теперь нам надо перейти от потенциалов к напряженностям полей, следовательно, возникает математическая проблема: мы должны дифференцировать потенциалы, но у нас разное время в левой и правой части. Таким образом надо научиться дифференцировать функции с запаздывающим потенциалом. Это отдельная задача, которая выходит за рамки нашего курса электродинамики.

А сейчас найдем потенциалы Лиенара – Вихерта с помощью преобразования Лоренца, чтобы убедиться в правильности наших убеждений.

б) Метод преобразований Лоренца для получения потенциалов.

Для покоящегося заряда: кулоновский потенциал и кулоновское поле. Идея: провести преобразования Лоренца из системы покоя заряда (штрихованная система), где потенциал известен, в лабораторную систему. Преобразования Лоренца в общем случае:

тогда

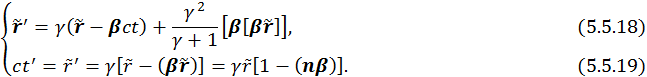
Используя то, что , получим:

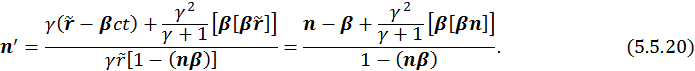
В системе покоя имеем векторный потенциал, равный

Т. к. все четырехмерные векторы преобразуются одинаково, получаем

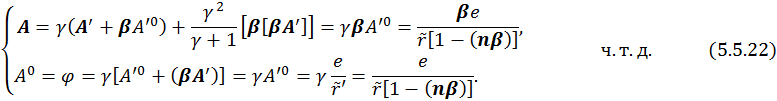
в) Метод преобразований Лоренца для напряженности полей.

В системе покоя у произвольно движущегося заряда есть только кулоновское поле

Учитывая преобразования Лоренца, для напряженностей полей с учетом (5.5.23) получим:

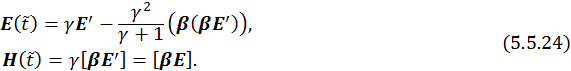
Для электрического поля имеем:

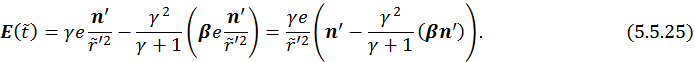
Подставим в (5.5.25) через :

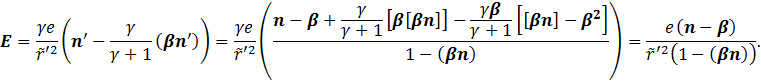
В итоге получаем выражение для электрического поля:

Тогда напряженность магнитного поля:

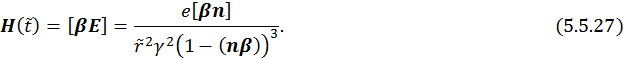
г) напряженности полей равномерно и прямолинейно движущегося заряда.

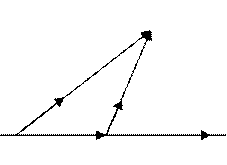
Покажем, что эта формула действительно совпадает с (5.5.26).

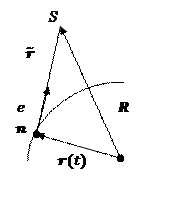
Согласно нашему рисунку

где 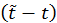– время, в течение которого движется заряд пока свет достигнет точки наблюдения.

Из формулы (5.5.30) следует, что

Подставляем (5.5.30) в (5.5.32) и получим:

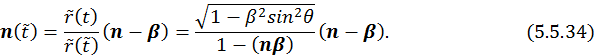
С учетом (5.5.33) и (5.5.34) уравнение (5.5.28) перепишется в виде:

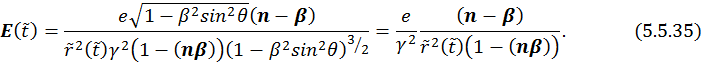
В итоге получаем выражение для электрического поля

которое совпадает с (5.5.26).

Напряженность магнитного поля:

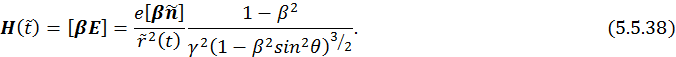
При 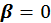выражение (5.5.27) будет равно нулю, как и должно быть.

Эти векторы обладают интересным свойством:

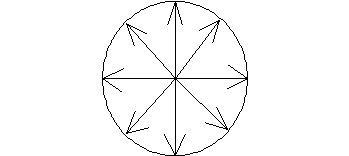
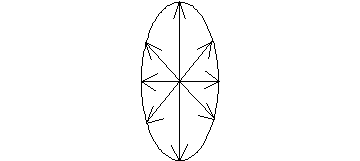
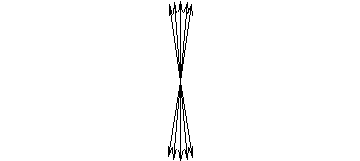
Анализ формулы (5.5.37) показывает, что с увеличением скорости в продольном направлении поле сжимается, а в поперечном увеличивается. Наглядно это можно показать следующим образом: