Прикладные методы решения задач теории упругости

ЛЕКЦИЯ 3 ПРИКЛАДНЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ ТЕОРИИ УПРУГОСТИ

1 Метод Ритца-Тимошенко

2 Метод Бубнова-Галеркина

3 Метод Власова-Канторовича

4 Метод Папковича-Треффца

5 Конечно-разностные методы

1 Метод Ритца-Тимошенко

Метод, предложенный В. Ритцем и распространенный С. П. Тимошенко на задачи строительной механики, позволяем получить приближенное (а в отдельных случаях и точное) решение в перемещениях на основе вариационного принципа Лагранжа изложенного в разд. 1.3. Идею метода, который относится к классу континуальных, поясним на примере решения пространственной задачи теории упругости.

Для построения приближенного решения три перемещения 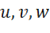представим в виде следующих рядов

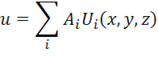
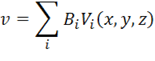
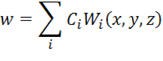
В (1.70) функции 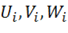называются аппроксимирующими и выбираются заранее. Внося (1.70) в выражение полной энергии (1.30) и выполняя интегрирование, получим

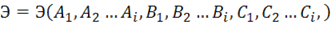
Поскольку полная энергия превратилась таким образом в функцию от коэффициентов, то условие минимума ее, следующее из принципа Лагранжа, будет реализоваться обращением в нуль всех производных от полной энергии по коэффициентам рядов (1.70), т. е. разрешающая система уравнений будет иметь вид:

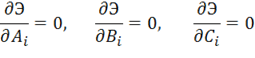
Поскольку полная энергия есть квадратичная функция от перемещений, то уравнения (1.71) будут представлять собой систему линейных алгебраических уравнений, причем количество этих уравнений всегда будет равно количеству членов (коэффициентов), вводимых в рядах (1.70) и, следовательно, система (1.71) будет полной относительно определяемых коэффициентов. Найдя в результате решения этой системы коэффициенты 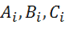можно далее по формуле (1.70) определить перемещения, а затем деформации и напряжения, т. е. получить полное решение задачи.

Таким образом, основная идея метода, кардинально упрощающая решение и, естественно, определяющая его приближенный характер, связана с тем, что искомые перемещения отыскиваются в классе заранее заданных функций, которые выбираются на основе опыта, интуитивно или на основе решений более простых задач. В результате минимизации полной энергии отыскивается распределение перемещений, наиболее близкое к истинному в энергетическом смысле, а в некоторых случаях может быть найдено и истинное поле перемещений, если оно содержится в заданном классе функций. Отметим, что на аппроксимирующие функции должны быть наложены определенные ограничения. Как следует из (1.30), они должны быть дифференцируемыми и поскольку принцип Лагранжа предусматривает сравнение кинематически возможных систем перемещений – удовлетворять геометрическим граничным условиям. При этом возникает и чисто математический вопрос о правомочности представления искомых функций в виде рядов, связанных с полной системы аппроксимирующих функций и сходимостью процесса при увеличении числа членов в рядах к точному решению. При практических расчетах эти вопросы поднимаются редко и в лучшем случае подменяются сравнением результатов при увеличении числа аппроксимирующих функций.

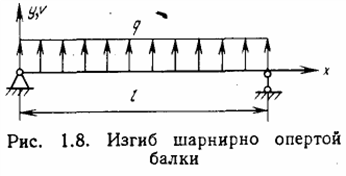
Пример. Рассмотрим изгиб шарнирно опертой балки постоянной жесткости под действием равномерно распределенной нагрузки (рис. 1.8). Геометрические граничные условия в этой задаче имеют следующий вид: при и .

Чтобы удовлетворить им, выберем аппроксимирующие функции в виде синусоид с целым числом полуволн п:

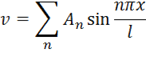
Полная энергия изгибаемой балки определяется равенством (1.33) при 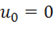, т. е.

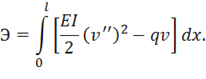
Внося выражение (1.72) и интегрируя, получим

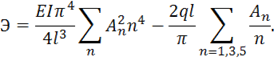
Система уравнений (1.71) принимает вид

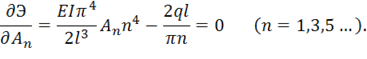
Отсюда

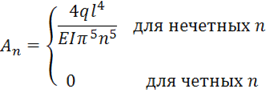
Таким образом, прогиб определяется равенством

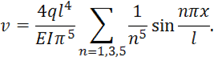
Для анализа сходимости ряда (1.73) рассмотрим прогиб балки в среднем сечении. Внося в (1.73) значение , получим

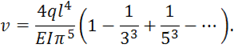
Отсюда видно, что ряд быстро сходится, его второй член составляет лишь 0,41% от первого. Здесь полезно отметить, что сходимость построенного ряда падает при его дифференцировании. Так, например, нормальное напряжение будет определяться через вторую производную от прогиба, для которой ряд будет иметь следующий вид:

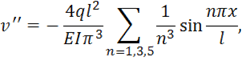
что для среднего сечения дает

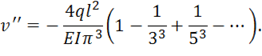
Здесь второй член составляет уже 3,7% от первого.

2 Метод Бубнова-Галеркина

Приближенный метод решения задачи путем сведения ее к системе линейных алгебраических уравнений, основанный на принципе возможных перемещений, был построен И. Г. Бубновым и весьма широко использовался при решении различных задач строительной механики Б. Г. Галеркнным. В рамках этого метода перемещения по-прежнему задаются в форме (1.70), и поскольку аппроксимирующие функции должны удовлетворять геометрическим граничным условиям и быть непрерывны внутри области, занятой материалом конструкции, они являются возможными формами перемещений и могут быть использованы для записи возможной работы всех сил. В рамках трехмерной задачи, используя уравнения (1.29), применяя в них 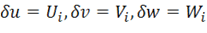и в силу произвольности функций перемещений 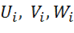приравнивая нулю возможную работу на каждом из этих перемещений, получим

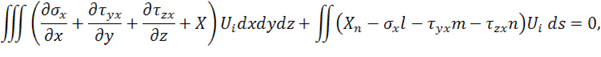
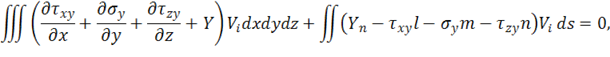
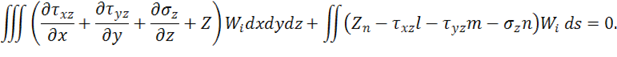
В уравнениях (1.74), естественно, понимается, что функции напряжений в соответствии с законом Гука и формулами Коши заменяются функциями перемещений, которые и представляются рядами (1.70). Представленный уравнениями (1.74) метод решения обычно называют обобщенным методом Бубнова–Галеркина, в рамках которого на аппроксимирующие функции накладывается требование удовлетворения геометрическим граничным условиям.