Происхождение магнитно-статистических полей

Теперь рассмотрим некоторые примеры взаимодействий с учетом того, что внешнее поле создается другой системой зарядов.

а) Взаимодействие точечного диполя в поле, создаваемым одним зарядом, находящимся в начале координат.

Тогда энергия дипольного момента в кулоновском поле заряда согласно (4.3.18) и (4.4.7) имеет вид:

б) Взаимодействие точечного диполя с электрическим полем другого диполя.

Пусть в начале координат находится дипольный момент , который создает внешнее поле, а – другой дипольный момент.

в) Сила, действующая на нейтральную систему с постоянным электрическим дипольным моментом (ЭДМ) со стороны неоднородного внешнего электрического поля.

Согласно общим правилам ньютоновской механики, сила есть

Если подставить сюда потенциальную энергию электрического диполя, то (4.4.12) примет вид:

Т. к. дипольный момент является постоянной величиной, то оператор набла действует только на вектор напряженности электрического поля:

Где согласно (3.1.7)

но магнитное поле отсутствует, следовательно, сила будет равна

г) Момент сил, действующих на нейтральную систему с электрическим дипольным моментом.

Момент сил имеет вид:

В качестве подставим (4.5.16). Тогда (4.5.17) преобразуется в

где

В линейном приближении по получим, что момент сил будет равен

Здесь – напряженность электрического поля в начале координат. Дипольный момент не зависит от выбора начала координат, следовательно,

§ 4.5. Происхождение магнитно-статистических полей

1.  Поля, создаваемые постоянным электрическим током.

Происхождение магнитного поля очевидно: оно создается движущимися зарядами. Т. к. вектор скорости зарядов меняется со временем, т. е. 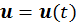, то магнитное поле будет тоже переменным по времени. Однако если система содержит много зарядов, и все они совершают стационарное установившееся движение, то после усреднения по времени можно получить поле, которое будет постоянным. Для определения среднего поля воспользуемся уравнениями Максвелла для магнитного поля из первой (3.1.7) и второй (3.4.11) пары:

Согласно общему правилу, среднее по времени равно

Здесь – период времени. Чем больше , тем точнее формула.

т. к. усреднение проводится по координатам быстродвижущихся зарядов, а дивергенция берется по координатам точки наблюдения. Точно также

Кроме того

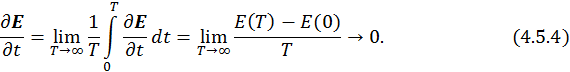
Если само поле меняется в конечных пределах, то при 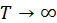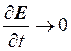. Этот результат известен как теорема о среднем значении производной от некоторой величины, которая меняется в конечных пределах. С учетом этой теоремы можно записать, что

Таким образом, мы получили выражения для средних значений:

Введем средний векторный потенциал согласно правилу:

Тогда если (4.5.7) подставить в (4.5.5), то

где 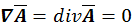– кулоновская калибровка потенциала. В итоге получаем:

Отсюда согласно (4.5.6) получаем

По аналогии со скалярным потенциалом 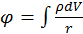можно найти решение для векторного потенциала:

Тогда средний вектор напряженности магнитного поля равен:

где ротор берется по координатам точки наблюдения, а не зарядов. Поэтому

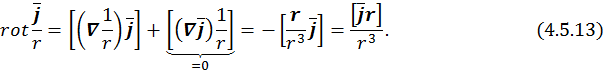
Подставляя (4.5.13) в (4.5.12), получим, что

Если речь идет о кривом проводнике с током, тогда плотность тока будет равна:

где – средняя скорость движения зарядов внутри проводника. Согласно рисунку

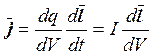. (4.5.16)

Подставим (4.5.16) в (4.5.12). Если ток постоянный, то его можно вынести за знак интеграла. Тогда получим, что

Здесь 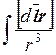– криволинейный интеграл, который берется по контуру с током.

2.  Поле магнитного диполя.

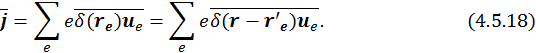
Тогда векторный потенциал будет равен:

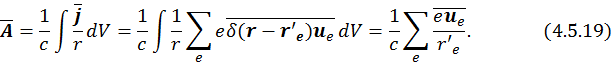
Раскладывая в ряд по малым , получим

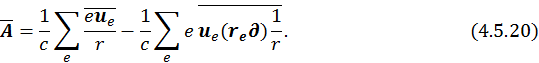
Согласно теореме о среднем значении производной по времени от функции, которая меняется в конечных пределах, первый член выражения (4.4.20) равен нулю, т. к. .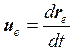

В итоге имеем:

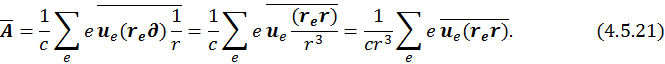
Т. к.

Распишем 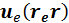и подставим формулу (4.5.22):

С учетом соотношения (4.5.24) примет вид:

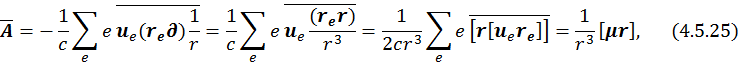
где – магнитный дипольный момент системы:

Векторный потенциал запишется в виде:

Напряженность магнитного поля определяется выражением (4.5.7). Раскрывая там двойное векторное произведение, получим

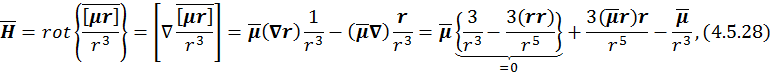
следовательно,

Линии напряженности магнитного поля имеют ту же конфигурацию, что и линии электрического поля. Магнитный дипольный момент является внутренней характеристикой данной системы стационарно движущихся зарядов. Поэтому эта характеристика не зависит от выбора системы координат.

Замечание: найдем связь между магнитным моментом системы зарядов и механическим. Согласно определению (4.5.26)

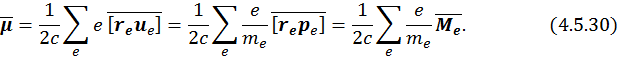
Если все заряды одинаковы по величине, а массы движущихся частиц совпадают, то для всех этих зарядов выполняется следующее соотношение:

где 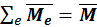– полный механический момент системы. Таким образом, получаем гиромагнитное отношение:

Обратим внимание на то, что для отдельного же электрона гиромагнитное отношение примет другой вид:

§ 4.6. Система зарядов во внешнем магнитном поле

Рассмотрим систему зарядов, находящихся в слабом, неоднородном и постоянном во времени внешнем магнитном поле.