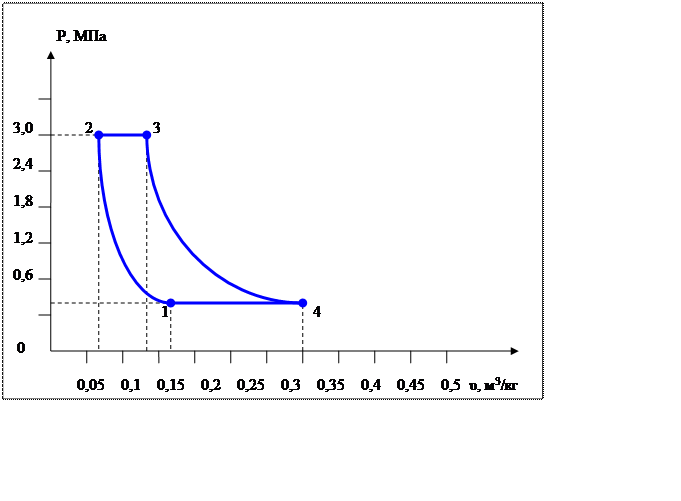
Расчет газового цикла
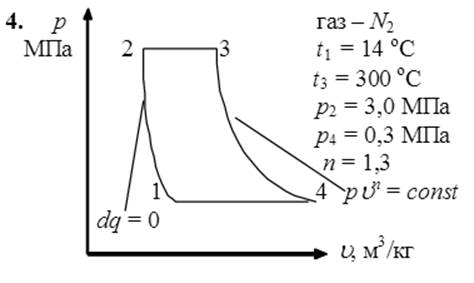
Рассмотрим обратимый цикл, который совершает воздух. Процессы цикла:
1-2 – адиабатное сжатие;
2-3 – изобарный нагрев;
3-4 – политропное расширение;
4-1 – изобарное сжатие;
РАСЧЕТ ГАЗОВОГО ЦИКЛА
|
Точки процессов |
Р, МПа |
υ, м3/кг |
Т, К |
u, кДж/кг |
i, кДж/кг |
|
1 |
0,3 |
0,284 |
287 |
207,788 |
293,027 |
|
2 |
3,0 |
0,055 |
561 |
406,164 |
572,781 |
|
3 |
3,0 |
0,056 |
573 |
414,852 |
585,033 |
|
4 |
0,3 |
0,329 |
337 |
243,988 |
344,077 |
В рυ координатах дан цикл, состоящий из нескольких термодинамических процессов, где отмечены исходные параметры отдельных точек (pi , υi, Ti ) и процессов (n, ∆s, q). На их основе необходимо вычислить неизвестные параметры состояния по характеристическому уравнению состояния для 1 кг заданного газа:
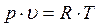 (1.1)
(1.1)
где p – абсолютное давление, Па; υ – удельный объем, м3/кг; R – газовая постоянная, Дж/(кг∙К); T – абсолютная температура, К.
Газовая постоянная определяется по формуле:
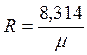 (1.2)
(1.2)
где μ – молекулярная масса газа, кг/моль.
Для политропических процессов показатель политропы n можно вычислить по формуле (например, для процесса 1-2):
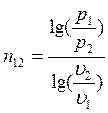 (1.3)
(1.3)
Удельные значения внутренней энергии и энтальпии определяются по выражениям:
, (1.4)
где 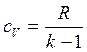 – изохорная удельная теплоемкость, кДж/(кг∙К);
– изохорная удельная теплоемкость, кДж/(кг∙К); 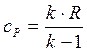 – изобарная удельная теплоемкость газа, кДж/(кг∙К). Значения показателя адиабаты k принять равными: для одноатомного газа – 1,67; для двухатомного газа — 1,41; для трехатомного и многоатомных газов – 1,33.
– изобарная удельная теплоемкость газа, кДж/(кг∙К). Значения показателя адиабаты k принять равными: для одноатомного газа – 1,67; для двухатомного газа — 1,41; для трехатомного и многоатомных газов – 1,33.
В точке 1: по условию t1 = 14°С = 287К; по условию процесс 4-1 – изобарный, поэтому р4 = р1 = 0,3МПа. Газовая постоянная для воздуха равна (согласно (1.2)): 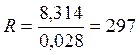 Дж/(кг∙К); тогда из уравнения (1.1) находим удельный объем азота в точке 1:
Дж/(кг∙К); тогда из уравнения (1.1) находим удельный объем азота в точке 1: 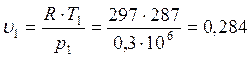 м3/кг;
м3/кг;
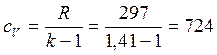 Дж/(кг∙К);
Дж/(кг∙К); 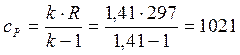 Дж/(кг∙К) → согласно (1.4):
Дж/(кг∙К) → согласно (1.4):
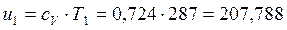 кДж/кг, кДж/кг;
кДж/кг, кДж/кг;
В точке 2: по условию р2 = 3,0МПа; процесс 1-2 – адиабатный, поэтому из уравнения Пуассона получаем:
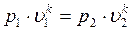 →
→ 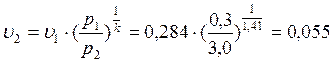 м3/кг;
м3/кг;
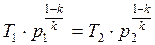 →
→ 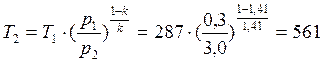 К;
К;
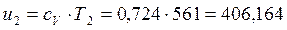 кДж/кг, кДж/кг;
кДж/кг, кДж/кг;
В точке 3: по условию р3 = р2 = 3,0МПа, Т3 = 573К; процесс 2-3 изобарный, поэтому из уравнения процесса: 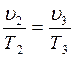 →
→ 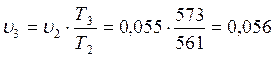 м3/кг;
м3/кг;
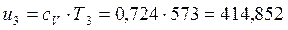 кДж/кг, кДж/кг;
кДж/кг, кДж/кг;
В точке 4: процесс 4-1 – изобарный, поэтому: ![]() МПа; процесс 3-4 политропный, поэтому:
МПа; процесс 3-4 политропный, поэтому: ![]() →
→ 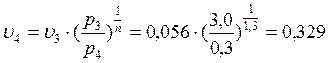 м3/кг;
м3/кг; ![]() →
→ 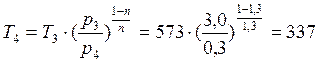 К;
К;
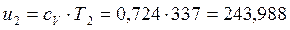 кДж/кг, кДж/кг;
кДж/кг, кДж/кг;
Изменения удельной внутренней энергии и удельной энтальпии для каждого процесса, входящего в цикл, определяются по формулам (например, для процесса 1-2):
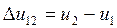 ,
, 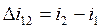 (1.5)
(1.5)
где значения u и i берутся из таблицы 1.1.
Для всех процессов изменение удельной энтропии ∆s , удельную работу изменения объема газа l , удельное количество теплоты q , показатель политропы n , теплоемкость политропного процесса c определяют по известным формулам, данным в литературных источниках.
Доля тепла расходуемого в рассматриваемом процессе на изменение внутренней энергии газа и работу изменения объема определяется по формулам:
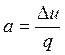 , (1.6)
, (1.6)
|
Процессы |
n |
C, кДж/(кг∙К) |
∆u, кДж/кг |
∆i, кДж/кг |
∆s, кДж/(кг∙К) |
q, кДж/кг |
l, кДж/кг |
a |
b |
|
1-2 |
1,41 |
0 |
198,376 |
279,754 |
0 |
0 |
-198,376 |
∞ |
— ∞ |
|
2-3 |
0 |
1,021 |
8,688 |
12,252 |
0,022 |
11,688 |
3 |
0,743 |
0,257 |
|
3-4 |
1,3 |
-0,265 |
-170,864 |
-240,956 |
0,142 |
54,909 |
225,773 |
— 3,112 |
-4,112 |
|
4-1 |
0 |
1,021 |
-36,2 |
-51,05 |
-0,164 |
-49,7 |
-13,5 |
0,728 |
0,272 |
Теплоемкость политропного процесса: 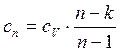 (1.7)
(1.7)
Согласно (1.5):
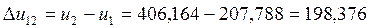 кДж/кг,
кДж/кг, 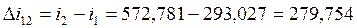 кДж/кг;
кДж/кг;
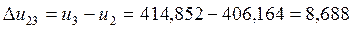 кДж/кг,
кДж/кг, 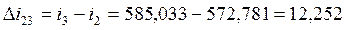 кДж/кг;
кДж/кг;
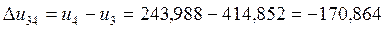 кДж/кг,
кДж/кг, 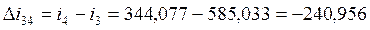 кДж/кг;
кДж/кг;
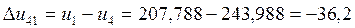 кДж/кг,
кДж/кг, 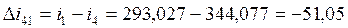 кДж/кг;
кДж/кг;
Согласно (1.3):
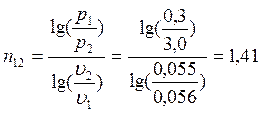 ;
; 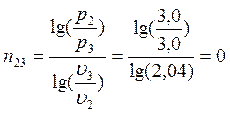 ;
;
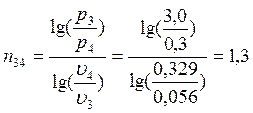 ;
; 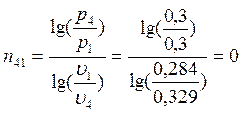 ;
;
Изменение энтропии процессов:
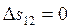 ;
; 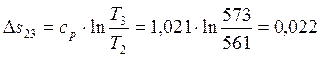 кДж/(кг∙К);
кДж/(кг∙К);
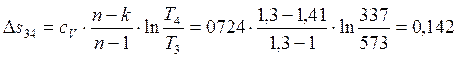 кДж/(кг∙К);
кДж/(кг∙К);
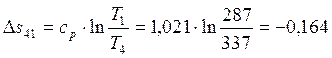 кДж/(кг∙К);
кДж/(кг∙К);
Работа в процессах:
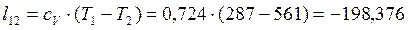 кДж/кг;
кДж/кг; 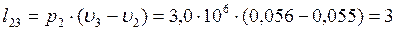 кДж/кг;
кДж/кг;
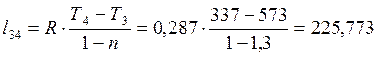 кДж/кг;
кДж/кг; 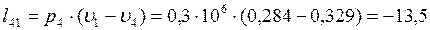 кДж/кг;
кДж/кг;
Согласно первому закону термодинамики теплота процессов равна: 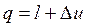 (1.8)
(1.8)
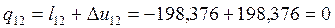 кДж/кг;
кДж/кг; 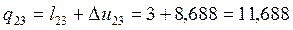 кДж/кг;
кДж/кг; 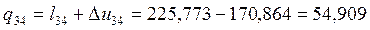 кДж/кг;
кДж/кг; 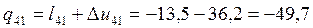 кДж/кг;
кДж/кг;
Согласно (1.6):
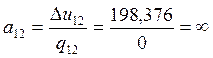 , ;
, ; 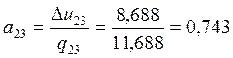 , ;
, ; 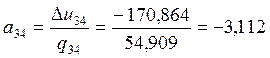 , ;
, ;
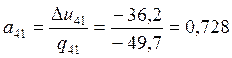 ; ;
; ;
Проверяем правильность вычислений:
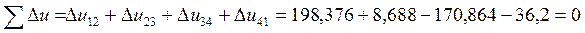 — верно;
— верно;
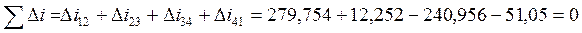 — верно;
— верно;
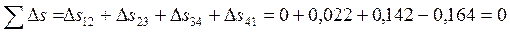 — верно;
— верно;
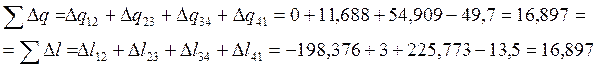 — верно;
— верно;
КПД цикла равен: 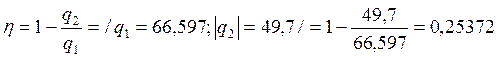 ;
;