Расчет магнитных полей с помощью векторного потенциала
3. Дан прямой длинный проводник, по которому течет ток I. Найдите индукцию магнитного поля в точке наблюдения, находящейся на расстоянии r от провода, считая, что он находится в среде с магнитной проницаемостью ![]() .
.
4. Найдите индукцию магнитного поля в коаксиальном кабеле, используемом для передачи постоянного тока. Ток течет по центральной жиле и возвращается по оболочке. Радиус центральной жилы r1, внутренний и внешний радиусы оболочки – r2 и r3. Пространство между жилой и оболочкой заполнено диэлектриком.
5. Точечный заряд ![]() движется со скоростью
движется со скоростью ![]() . Покажите, что в произвольной точке наблюдения
. Покажите, что в произвольной точке наблюдения 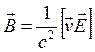 .
.
Дополнительный блок задач
6. Дан круговой виток радиусом ![]() с током
с током ![]() . Найдите интеграл
. Найдите интеграл ![]() вдоль оси витка в пределах от
вдоль оси витка в пределах от ![]() до
до ![]() .
.
7. Дан бесконечный полый цилиндр. Ток ![]() равномерно распределен по поверхности цилиндра и направлен вдоль его оси. Найдите индукцию магнитного поля на оси цилиндра.
равномерно распределен по поверхности цилиндра и направлен вдоль его оси. Найдите индукцию магнитного поля на оси цилиндра.
8. Определите магнитную индукцию в центре шара радиуса ![]() , равномерно покрытого очень большим числом
, равномерно покрытого очень большим числом ![]() витков тонкой проволоки, по которой течет ток
витков тонкой проволоки, по которой течет ток ![]() .
.
9. Сфера радиуса ![]() , имеющая заряд с поверхностной плотностью
, имеющая заряд с поверхностной плотностью ![]() , вращается вокруг диаметра с угловой скоростью
, вращается вокруг диаметра с угловой скоростью ![]() . Найдите индукцию магнитного поля, возникающего в центре сферы.
. Найдите индукцию магнитного поля, возникающего в центре сферы.
10.Принимая орбиту электрона в невозбужденном атоме водорода за окружность радиуса 53 пм, определите индукцию магнитного поля, создаваемого им в центре орбиты.
11.Однородный ток плотности ![]() течет внутри неограниченной пластины толщиной
течет внутри неограниченной пластины толщиной ![]() параллельно ее поверхности. Пренебрегая влиянием вещества пластины, найдите индукцию магнитного поля этого тока как функцию расстояния от средней плоскости пластины.
параллельно ее поверхности. Пренебрегая влиянием вещества пластины, найдите индукцию магнитного поля этого тока как функцию расстояния от средней плоскости пластины.
12.Точечный заряд движется со скоростью 900 м/с. В некоторый момент в точке наблюдения Р напряженность поля этого заряда составляет 600 В/м, а угол между скоростью движения и напряженностью составляет 30º. Найдите индукцию магнитного поля, создаваемого этим зарядом в точке наблюдения.
13.Пусть два положительных точечных заряда ![]() и
и ![]() движутся параллельно друг другу с одинаковой скоростью
движутся параллельно друг другу с одинаковой скоростью ![]() . Найдите отношение магнитной силы к электрической, действующей со стороны первого заряда на второй.
. Найдите отношение магнитной силы к электрической, действующей со стороны первого заряда на второй.
14.Дан длинный соленоид, имеющий N витков и длину l. Магнитная проницаемость сердечника ![]() . Найдите индукцию магнитного поля внутри соленоида, считая, что его поле внутри однородно, а вне – равно 0.
. Найдите индукцию магнитного поля внутри соленоида, считая, что его поле внутри однородно, а вне – равно 0.
15. На сердечнике в виде тора диаметром d имеется обмотка с общим числом витков N. В сердечнике есть узкая прорезь шириной b. При токе I в обмотке магнитная индукция в прорези B0. Найдите магнитную проницаемость сердечника.
Практическое занятие №7
Расчет магнитных полей с помощью векторного потенциала
Решение прямой и обратной задач магнитостатики
Краткие теоретические сведения
Для решения системы уравнений Максвелла в магнитостатическом случае вводится понятие векторного потенциала ![]() , который определяется как решение уравнения
, который определяется как решение уравнения
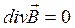 , (7.1)
, (7.1)
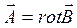 . (7.2)
. (7.2)
На векторный потенциал для однозначности определения накладывается ограничение – кулоновская калибровка
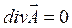 . (7.3)
. (7.3)
Решение системы дает нам уравнение Пуассона
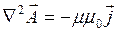 , (7.4)
, (7.4)
где ![]() – вектор плотности тока.
– вектор плотности тока.
В соответствии с определением 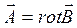 векторный потенциал в общем случае можно рассчитать как
векторный потенциал в общем случае можно рассчитать как
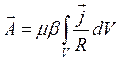 . (7.5)
. (7.5)
Прямой задачей магнитостатики является расчет векторного потенциала и индукции магнитного поля по известному распределению токов, а обратной – нахождение распределения токов по известному векторному потенциалу.
Темы для развернутых ответов
1. Векторный потенциал. Пояснить связь с индукцией магнитного поля.
2. Уравнение Пуассона для векторного потенциала. Привести пример решения.
Литература: [1], глава 6, §37; [3], глава 4, §46-47.
Основной блок задач
1. В сферических координатах две компоненты векторного потенциала равны нулю 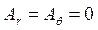 , а третья имеет вид
, а третья имеет вид 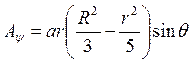 при
при ![]() и
и 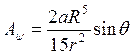 при
при ![]() , где
, где ![]() и
и ![]() – постоянные. Найдите распределение объемной плотности тока, создавшего магнитного поле с данным потенциалом.
– постоянные. Найдите распределение объемной плотности тока, создавшего магнитного поле с данным потенциалом.


