Расчетные выражения для скорости звука в общем виде
Разделим уравнение (1) на dT и умножим на Т при р=const. Тогда имеем:
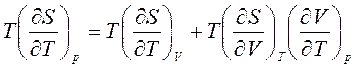 . (2)
. (2)
По определению 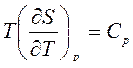 и
и 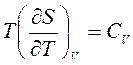 . После их подстановки в (2) получим:
. После их подстановки в (2) получим:
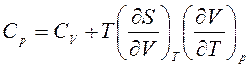 . (3)
. (3)
Производная 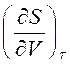 включает калорическую величину – энтропию и неудобна при расчетах. Поэтому заменим эту производную, используя соотношения взаимности Максвелла для смешанных производных от свободной энергии Гельмгольца:
включает калорическую величину – энтропию и неудобна при расчетах. Поэтому заменим эту производную, используя соотношения взаимности Максвелла для смешанных производных от свободной энергии Гельмгольца:
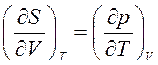 .
.
Тогда, используя уравнение связи в виде:
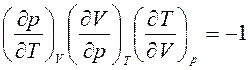 , получим:
, получим:
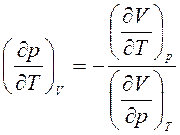 . (4)
. (4)
Подставим выражение (4) вместо 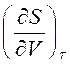 в (3) и получим:
в (3) и получим:
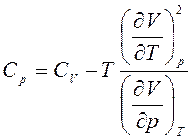 . (5)
. (5)
Покажем, как из уравнения (5) можно получить уравнение Майера для идеального газа, дифференцируя уравнение состояния:
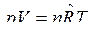 . Тогда
. Тогда 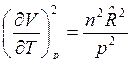 и
и 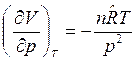 .
.
После подстановки этих производных в (5) получим:
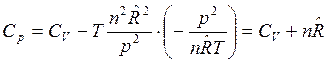 , Дж/К.
, Дж/К.
Таким образом, получили уравнение Майера для общих теплоемкостей Ср и СV системы:
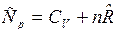 .
.
Получим связь между Ср и CV в другом виде, используя производные от натуральных логарифмов параметров и учитывая, что ![]() .
.
Тогда получим, что
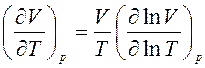 и
и 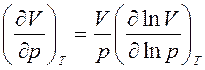 . (6)
. (6)
После подстановки выражений (6) в уравнение (5) с учетом, что 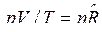 , окончательно получим связь между изобарной и изохорной теплоемкостями в общем виде:
, окончательно получим связь между изобарной и изохорной теплоемкостями в общем виде:
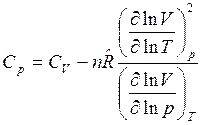 .
.
7.6.Расчетные выражения для скорости звука в общем виде
По определению адиабатная скорость звука равна:
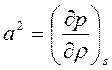 , (1)
, (1)
где плотность газа 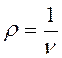 и
и 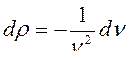 . Тогда:
. Тогда:
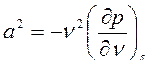 . (2)
. (2)
По уравнению связи частных производных одного параметра по другому имеем:
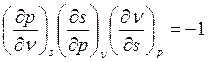 , откуда:
, откуда:
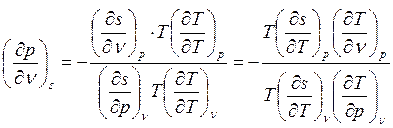 .
.
По определению изобарная и изохорная удельные теплоемкости равны:
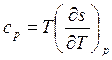 и
и 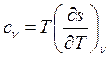 . Тогда
. Тогда
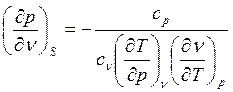 . (3)
. (3)
После подстановки выражения (3) в (2) имеем:
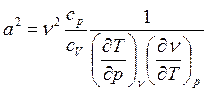 . (4)
. (4)
По уравнению связи:
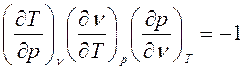 , имеем:
, имеем:
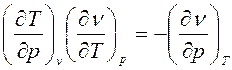 . (5)
. (5)
После подстановки выражения (5) в (4) окончательно имеем выражение для расчета скорости звука в общем виде:
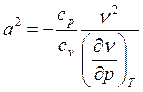 . (6)
. (6)
Из формулы (6) получим формулу для расчета скорости звука в идеальном газе при условии, что удельная газовая постоянная R не зависит от давления и температуры. Тогда из уравнения состояния для 1 кг идеального газа: ![]() , имеем
, имеем 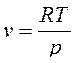 и производную
и производную 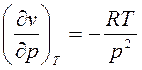 . После подстановки выражения для
. После подстановки выражения для ![]() в формулу (6) получим:
в формулу (6) получим:
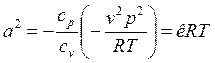 , где
, где 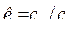 — показатель адиабаты,
— показатель адиабаты, ![]() . Тогда:
. Тогда: 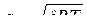 — скорость звука в идеальном газе.
— скорость звука в идеальном газе.
7.7. Максимальная и минимальная теплоты процесса
Уравнения первого закона термодинамики в сложных закрытых ТС при двух фиксированных параметрах имеют вид:
— для изохорно-изотермического процесса (T,V=const): 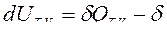 ℒТ,V ;
ℒТ,V ;
— для изобарно-изотермического процесса (T,p=const): 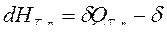 ℒТ, р.
ℒТ, р.
При написании этих уравнений использовалось правило знаков, принятое в термодинамике, т. е. 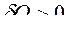 , если теплота подводится к ТС, и
, если теплота подводится к ТС, и ![]() ℒ>0, если работа совершается термодинамической системой. В термохимии принято противоположное правило знаков для теплоты, т. е. теплота
ℒ>0, если работа совершается термодинамической системой. В термохимии принято противоположное правило знаков для теплоты, т. е. теплота 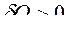 , (положительна), если она отводится от ТС. Тогда для конечных процессов 1-2 уравнение 1-го закона термодинамики будет иметь вид:
, (положительна), если она отводится от ТС. Тогда для конечных процессов 1-2 уравнение 1-го закона термодинамики будет иметь вид:


