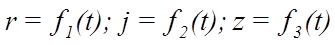Различные формы условий равновесия плоской системы сил
,
имеем три уравнения равновесия:
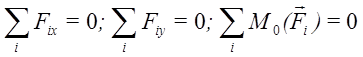
Рис.16
Для плоской системы параллельных сил (Рис. 17) имеем лишь два уравнения равновесия:
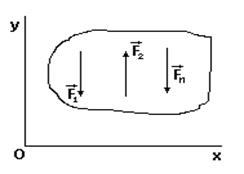
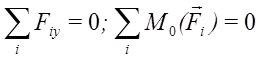
Рис.17
Различные формы условий равновесия плоской системы сил:
1. Ранее приведенная система
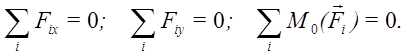
2. Эквивалентная ей система уравнений равновесия для любых трех точек, не лежащих на одной прямой.
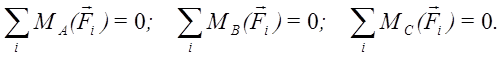
3. Также эквивалентная первой система
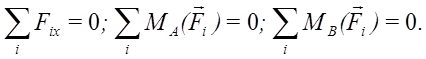
для любых точек А и В, если ось X не перпендикулярна отрезку АВ.
Для плоской системы параллельных сил имеем аналогичную систему уравнений равновесия 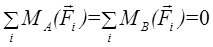 для любых точек А и В.
для любых точек А и В.
Статически определимые и неопределимые системы
Для любой системы сил для разрешимости задач необходимо, чтобы число неизвестных сил не превышало максимального числа возможных уравнений равновесия. Такие задачи называют статически определимыми. В противном случае задача будет статически неопределимой в рамках модели абсолютно твердого тела. Статически неопределимые задачи решаются методами механики твёрдого деформируемого тела.
2. КИНЕМАТИКА
2.1. Основные понятия
Кинематикой называется раздел механики, в которой изучаются геометрические свойства движения тел без учета их инертности (массы) и действующих на них сил.
Под движением мы понимаем в механике изменение с течением времени положения данного тела в пространстве по отношению к другим телам.
2.2. Кинематика точки. Скорость и ускорение точки
в декартовых координатах
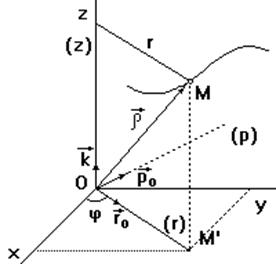
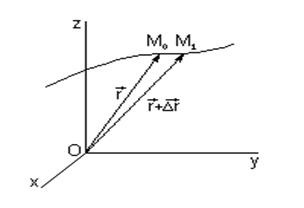 Положение точки М0 определяем радиус-вектором
Положение точки М0 определяем радиус-вектором ![]() (рис. 18). Если точка движется относительно системы отсчета Oxyz, то ее координаты будут функциями времени:
(рис. 18). Если точка движется относительно системы отсчета Oxyz, то ее координаты будут функциями времени:
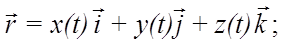
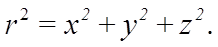
Рис. 18
Скорость и ускорение точки М в некоторый момент времени:
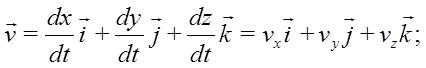
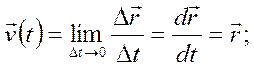
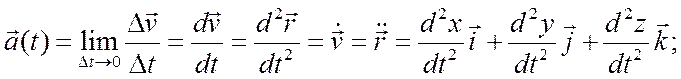
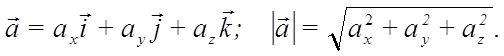
Обозначим через S длину дуги траектории, отсчитываемой с соответствующим знаком от первоначального положения точки на траектории:
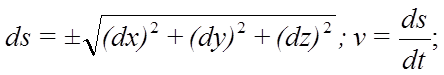
Тогда, очевидно,
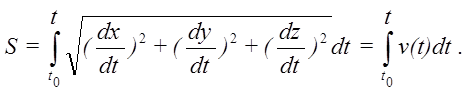
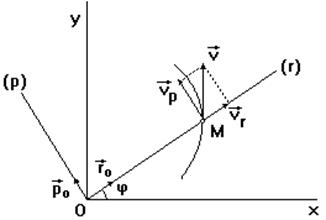
Годограф. К началу неподвижной системы координат О приложим вектор ОР, равный по величине и направлению скорости движущейся точки. При движении точки М по ее траектории точка Р описывает некоторую кривую, называемую годографом скорости точки М. Очевидно, скорость точки годографа Р равна по определению ускорению точки М.
2.3. Скорость и ускорение точки
в естественной системе координат
Определим орт 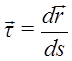 , он направлен по касательной к траектории. Вектор
, он направлен по касательной к траектории. Вектор ![]() ортогонален к орту
ортогонален к орту ![]() .
.
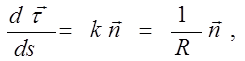
Составим отношение:
где k − кривизна траектории, R − радиус кривизны траектории.
Третий орт ![]() определим как
определим как 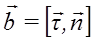
Определим скорость и ускорение точки в естественной системе координат:
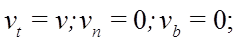
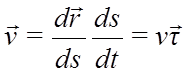
; то есть
Таким образом, скорость точки всегда направлена по касательной к траектории.
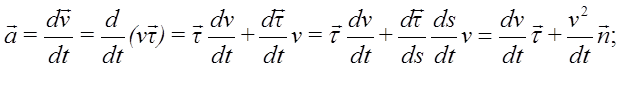
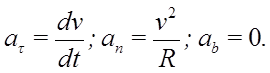
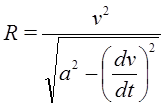 то есть
то есть
Из последних соотношений получим формулу:
2.4. Скорость и ускорение точки в полярных координатах
Положение точки на плоскости известно, если заданы радиус-вектор ![]() и полярный угол φ как функции времени (рис. 19):
и полярный угол φ как функции времени (рис. 19):
![]()
Введем единичный вектор ![]() , направленный по радиус-вектору от полюса О к точке М. Тогда
, направленный по радиус-вектору от полюса О к точке М. Тогда 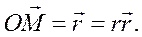
Для скорости получаем :
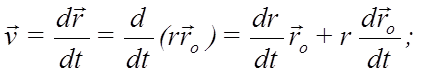
Рис. 19
Для производной по времени от единичного вектора имеем:
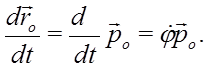
После этого для скорости точки в полярных координатах получаем:
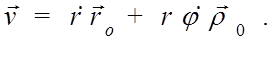
Таким образом, радиальная и трансверсальная составляющие вектора скорости имеют вид:
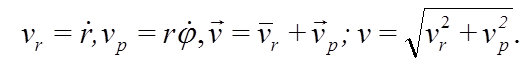
Для ускорения легко получить:
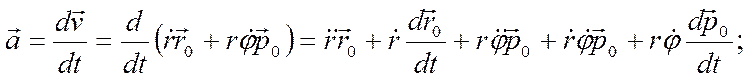
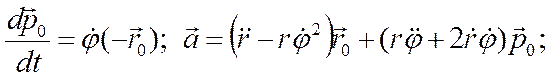
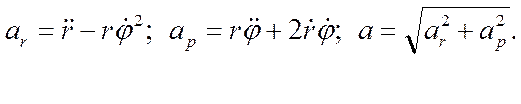
2.5. Скорость и ускорение точек в цилиндрических
координатах
Положение точки М в пространстве определяют заданием трех ее цилиндрических координат как функций времени (рис. 20):