Решение волнового уравнения
Контрольная работа
Задача 1. Решить первую смешанную задачу для волнового уравнения на отрезке.
![]()
![]()
Решение:
Запишем решение для волнового уравнения на отрезке длины ![]() для условий
для условий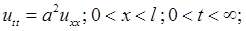
![]() :
:
![]()
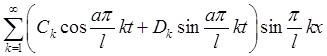 . Где
. Где 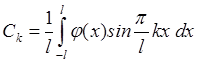 ,
,
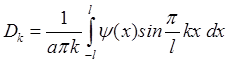 .
.
Для условий задачи после подстановки a и l будет следующее выражение:
![]()
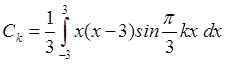 , все
, все ![]() равны нулю, т. к.
равны нулю, т. к. 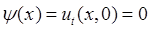 .
. ![]()
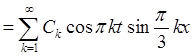 .
.
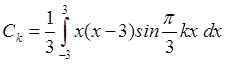 =
= 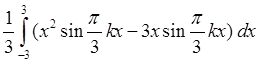 =
=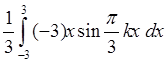 =
=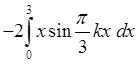 =
=
=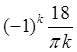 .
.
![]()
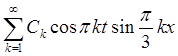 =
= 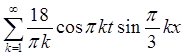 =
= 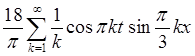 .
.
Ответ: ![]()
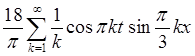 .
.
Задача 2. Решить первую смешанную задачу для волнового уравнения в прямоугольнике.
![]() .
.
Решение:
Запишем решение для волнового уравнения на прямоугольнике для условий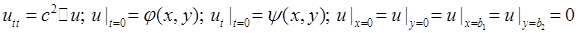 :
:
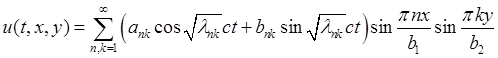 ;
;
![]() =
=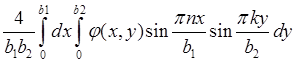 ;
;
![]() =
=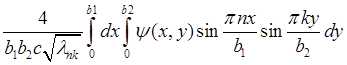 ;
;
![]() =
=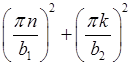 .
.
После подстановки условий задачи получится следующее выражение:
![]()
![]() , так как
, так как 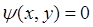 ;
;
![]() =
=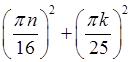 ;
;
![]() =
=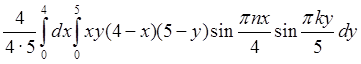 =
=
=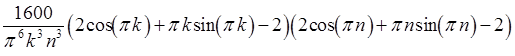 =
=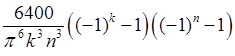 ;
;
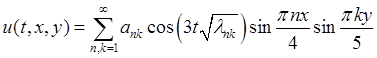 =
=
=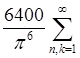
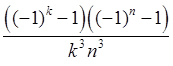
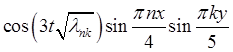 .
.
Ответ: ![]()
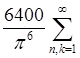
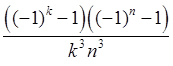
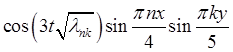 , где
, где ![]() =
=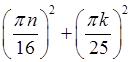 .
.
Задача 3. Решить первую смешанную задачу для волнового уравнения в круге.
![]()
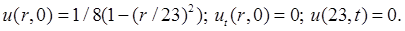
Решение:
Запишем решение для волнового уравнения в круге радиуса ![]() для условий
для условий 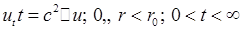 :
:
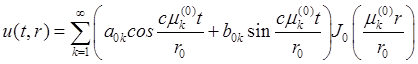 ;
;
![]() =
=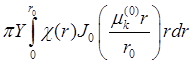 ;
;
![]() =
=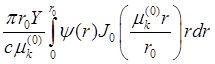 ;
;
Где ![]() =
=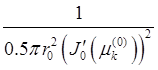 ,
, ![]() — функция Бесселя первого рода,
— функция Бесселя первого рода, ![]() — корень с номером
— корень с номером ![]() уравнения
уравнения ![]() =
=![]() (это уравнение имеет бесконечное число корней).
(это уравнение имеет бесконечное число корней).
Так как ![]()
![]()
![]() .
.
Подставляем значения из условия задачи в выражения для ![]() ,
, ![]() ,
,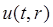 :
:
![]() =
=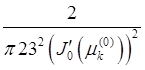
![]() =
=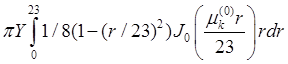 ;
;
![]() =
=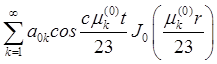 .
.
Ответ: ![]() =
=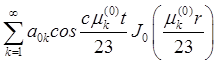 , где
, где ![]() =
=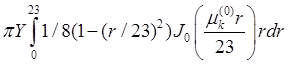 ,
,
![]() =
=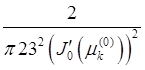 ,
, ![]() — функция Бесселя первого рода,
— функция Бесселя первого рода, ![]() — корень с номером
— корень с номером ![]() уравнения
уравнения ![]() =
=
=![]() .
.
Задача 4. Найти решение первой смешанной задачи для уравнения теплопроводности на отрезке.
![]() ;
; ![]() =
=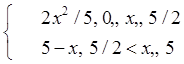 ;
; ![]() .
.
Решение:
Решим задачу для условий записанных ниже:
![]() ;
; 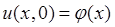 ;
; ![]() .
.
Применим метод разделения переменных Фурье. Будем искать частное решение уравнения в виде![]()
![]()
![]()
![]()
![]()
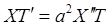
![]()
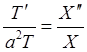 =
=![]() . После преобразования, получим два дифференциальных уравнения:
. После преобразования, получим два дифференциальных уравнения:
1)![]() ;
;
2)![]() .
.
Отыскание ![]() для второго уравнения представляет собой задачу Штурма – Луивилля, собственные значения которой
для второго уравнения представляет собой задачу Штурма – Луивилля, собственные значения которой 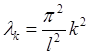 , а собственные функции
, а собственные функции 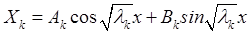 , где
, где ![]() целое и
целое и ![]() .
.
Решение первого уравнения следующее 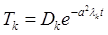 (используется индекс k, так как каждому
(используется индекс k, так как каждому ![]() соответствует свой
соответствует свой ![]() , и получается бесконечное счетное множество решений).
, и получается бесконечное счетное множество решений).
![]() =
=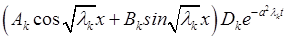 , где
, где ![]() частные решения уравнения
частные решения уравнения ![]() . Из граничных условий следует, что
. Из граничных условий следует, что 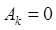 и
и ![]() , обозначим
, обозначим ![]() =
=![]() , и получим
, и получим
![]() =
=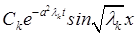 . Запишем общее решение как сумму частных
. Запишем общее решение как сумму частных 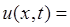
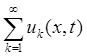 =
=
=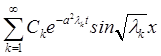 =
=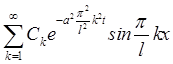 .
. ![]() определим из начальных условий
определим из начальных условий ![]() :
:
![]() =
=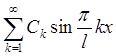 =. Отсюда видно, что
=. Отсюда видно, что ![]() являются коэффициентами разложения
являются коэффициентами разложения ![]() в ряд Фурье по синусам
в ряд Фурье по синусам ![]()
![]() =
= 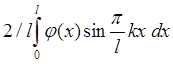 .
.
Найдем ![]() для условий нашей задачи:
для условий нашей задачи:
![]() =
= 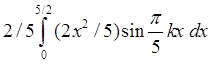 +
+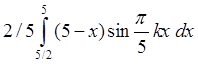 =
=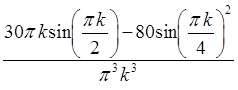
![]()
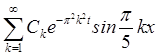 =
=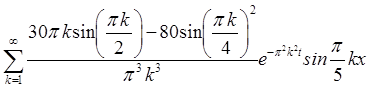 =
=
=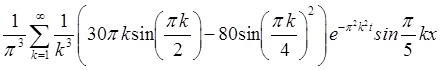 .
.
Ответ: ![]()
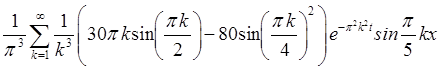 .
.
Задача 5. Найти решение первой смешанной задачи для уравнения теплопроводности в круге.
![]()
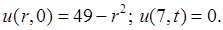
Решение:
Запишем решение для волнового уравнения в круге радиуса ![]() для условий
для условий 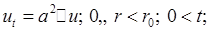
![]() в полярных координатах:
в полярных координатах:
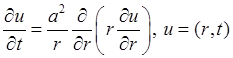 .
.
Будем искать частное решение в виде 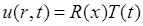 . Тогда
. Тогда 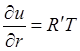 ,
,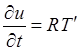
![]()
![]()
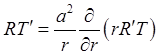
![]()
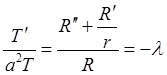 .Отсюда получаем два уравнения:
.Отсюда получаем два уравнения:
1)![]()
2)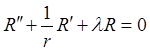 .
.
Решением задачи Штурма-Лиувилля для R будут собственные значения 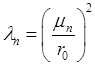 и собственные функции
и собственные функции 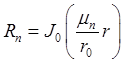 , где
, где ![]() — функция Бесселя первого рода нулевого порядка,
— функция Бесселя первого рода нулевого порядка,![]() — корни уравнения
— корни уравнения 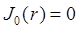 , n – целое число n > 0.
, n – целое число n > 0.
Соответствующие решения уравнения 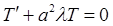 будут такими:
будут такими: 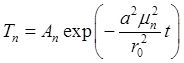 .
.
Тогда ![]() =
=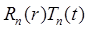 =
=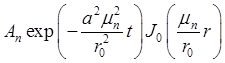 .
.
Общее решение будем искать в виде 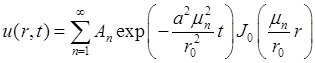 . Воспользуемся начальными условиями
. Воспользуемся начальными условиями 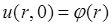 , подставив значение
, подставив значение ![]() и получим:
и получим: 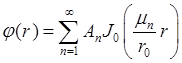
![]()
![]()
![]() — это коэффициенты Эйлера-Фурье разложения функции
— это коэффициенты Эйлера-Фурье разложения функции ![]() в ряд по
в ряд по 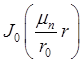
![]()
![]()
![]() =
= 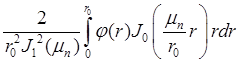 , где
, где ![]() — функция Бесселя первого рода первого порядка.
— функция Бесселя первого рода первого порядка.
В результате мы имеем:
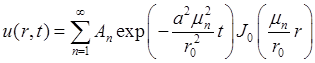 ,
, ![]() =
= 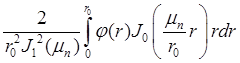 .
.
Подставим значения из условия задачи 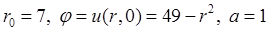 :
:
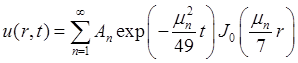 ,
, ![]() =
=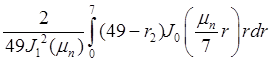 .
.
Ответ: 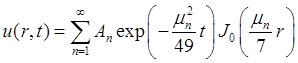 ,
, ![]() =
=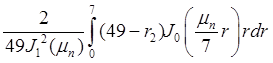 .
.
Задача 6. Используя формулу Пуассона, найти решения задачи Коши для уравнения теплопроводности.
![]() .
.
Решение:
Для условий ![]() формула Пуассона записывается в виде:
формула Пуассона записывается в виде:
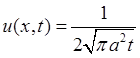
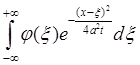 . У нас
. У нас ![]() . После подстановки значений в интеграл, получим:
. После подстановки значений в интеграл, получим:
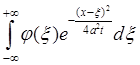 =
=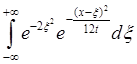 =
=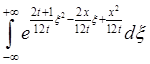 .
.
Результатом вычисления интеграла 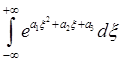 , где
, где 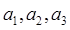 — константы, является выражение:
— константы, является выражение:
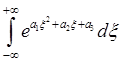 =
=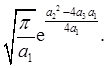 Для интеграла нашей задачи
Для интеграла нашей задачи 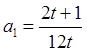 ;
; 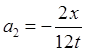 ;
; 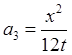 .
.
Тогда после преобразований 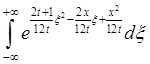 =
=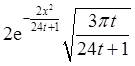 . Таким образом
. Таким образом
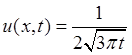
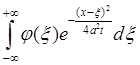 =
=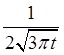
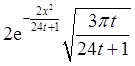 =
=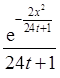 .
.
Ответ: ![]() =
=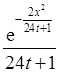 .
.
Задача 7. Найти общее решение уравнения.
![]() .
.
Решение:
Приведем уравнение, данное в условиях, к каноническому виду. Для этого составим характеристическое уравнение ![]() . Разрешим его относительно dy. Получим два уравнения
. Разрешим его относительно dy. Получим два уравнения 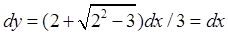 и
и ![]() . После интегрирования уравнения перейдут в
. После интегрирования уравнения перейдут в
1)![]()
2) ![]() .
.
Осуществим замену переменных ![]() .
.
Вычислим частные производные новых переменных по старым переменным: 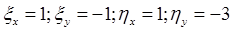 .
.
Так как ![]() выражаются линейно через
выражаются линейно через ![]() , то получим:
, то получим:
![]() ;
;
![]() ;
;
![]() ;
;
Подставим значения производных:
![]() =
= 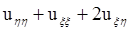 ;
;
![]() =
=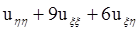 ;
;
![]() =
= 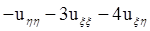 .
.
Из условия задачи получаем 0=![]() =
=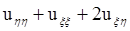 +
+![]()
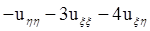 =
=![]() .
.
Общим решением полученного уравнения ![]() =0 (предполагается, что все вторые частные производные непрерывны) является функция линейная относительно переменных:
=0 (предполагается, что все вторые частные производные непрерывны) является функция линейная относительно переменных:
![]() , где
, где 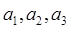 — произвольные константы. При возврате к независимым переменным x, y получится функция
— произвольные константы. При возврате к независимым переменным x, y получится функция ![]() , где
, где 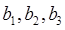 — произвольные константы.
— произвольные константы.
Ответ: ![]() , где
, где 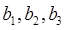 — произвольные константы.
— произвольные константы.
Задача 8. Решить смешанную задачу.
![]()
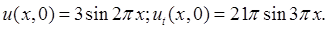
Решение:
Запишем решение для волнового уравнения на отрезке длины ![]() в общем виде:
в общем виде:
![]()
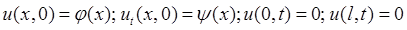 .
.
![]()
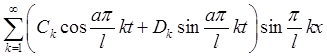 . Где
. Где 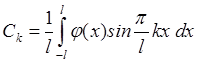 ,
,
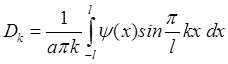 .
.
Для условий задачи после подстановки a и l будет следующее выражение:
![]()
![]()
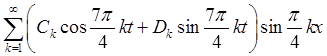 .
.
Так как 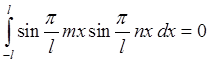 при
при 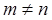
![]()
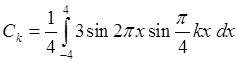 =
=
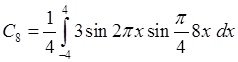
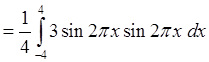 =3. При
=3. При ![]() .
.
Аналогично, для 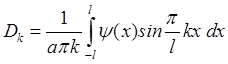 , получим
, получим ![]() =
=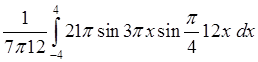 =1. При
=1. При 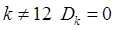 .
.
![]()
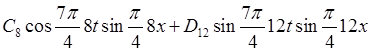 =
=
= 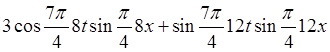 =
=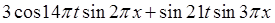 .
.
Ответ: ![]()
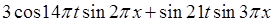 .
.


