Алгоритм решения осесимметричных задач дифракции методом зон Френеля

Рис. 6.6

Результирующее волновое поле представляется в виде ряда

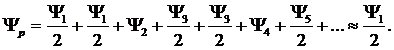. (6.5)

Здесь приближенно считается, что

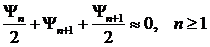
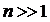и волновые поля приближенно равны 0 для . Следовательно, суммарный вклад большого числа зон Френеля в полное волновое поле равен половине вклада центральной первой зоны.

На основе этого результата можно более точно определить световой луч, идущий из источника S в точку наблюдения P. Площадь поперечного сечения этого луча принимается равной площади

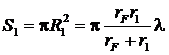(6.6)

первой зоны Френеля, где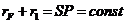, – расстояние между точками O и P на рис. 6.5 и

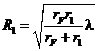
– радиус первой зоны Френеля (рис. 6.7). Иными словами, излучение от

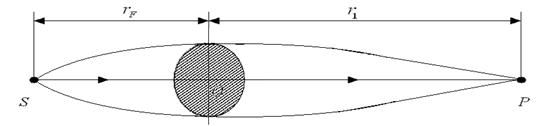
Рис. 6.7

источника S к точке наблюдения P в основном распространяется в пределах первой зоны Френеля переменного радиуса ().

Количественные результаты для осесимметричных задач дифракции получаются с помощью векторных диаграмм на основе специально построенной спирали, которая более детально описывает волновые поля отдельных зон Френеля. С целью получения этой спирали каждый вектор нечетной зоны Френеля на рис. 6.6 дополняется полуокружностью, расположенной справа от него, а каждый вектор четной зоны Френеля – полуокружностью, расположенной слева от него (рис. 6.8).

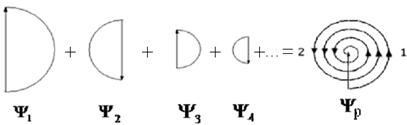
Рис. 6.8

Все эти полуокружности совмещаются таким образом, чтобы их центры находились на одной вертикальной прямой, они сами образовали непрерывную спираль, которая накручивается на конец результирующего вектора, описывающего суммарное волновое поле в точке наблюдения P. Напомним, что длина вектора в два раза меньше длины вектора .

Какой физический смысл имеют эти полуокружности? Если зону Френеля разбить на большое количество кольцевых подзон с одинаковой площадью, то векторы, описывающие волновое поле этих подзон в точке наблюдения P, образуют ломаную линию из векторов одинаковой длины, лежащую на соответствующей полуокружности (см. рис. 6.9 для центральной первой зоны Френеля).

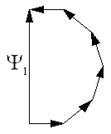
Рис. 6.9

Векторы отдельных подзон, сложенные по правилу треугольника, дают вектор, описывающий волновое поле всей зоны Френеля.

В осесимметричных задачах дифракции круглый непрозрачный диск или непрозрачный плоский экран с круглым отверстием закрывает для выбранной точки наблюдения часть зон Френеля на волновой поверхности, проходящей через диск или отверстие. Спираль на рис. 6.8 позволяет с помощью векторной диаграммы просуммировать вклады вторичных волн всех открытых зон Френеля. Если первичная волна является плоской, то число зон Френеля , которое помещается на круге радиусом r, описывается формулой

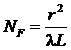, (6.7)

где λ – длина волны, L – расстояние от центра круга до точки наблюдения. Величина называется числом Френеля и используется для оценки числа открытых (случай круглого отверстия в экране) или закрытых (случай непрозрачного круглого диска) зон Френеля.

Алгоритм решения осесимметричных задач дифракции методом зон Френеля

1.  Нарисовать спираль, описывающую действие всех зон Френеля.

2.  Отметить (например, штриховкой) те участки спирали, которые соответствуют закрытым зонам.

3.  Построить вектор, соединяющий начало нештрихованной части спирали с ее концом.

4.  Сравнить полученный вектор по величине и ориентации с вектором, описывающим действие всех зон в точке наблюдения в отсутствие препятствия и сделать вывод о том, как препятствие на пути распространения волны повлияло на ее интенсивность и фазу в точке наблюдения. Изменение длины вектора соответствует изменению амплитуды волны, а угол поворота вектора – сдвигу фазы дифрагированной волны. Интенсивность волны пропорциональна квадрату амплитуды.

Применим этот алгоритм для анализа исторического опыта Араго, сыгравшего важную роль в признании волновой теории света. Если на пути световой волны поставить непрозрачный диск перпендикулярно к направлению её распространения, то в точке наблюдения на оси симметрии всегда имеется светлое пятнышко. Если диск закрывает первые n1 зон Френеля, то все остальные зоны Френеля с n > n1 являются открытыми и их вторичные волны в точке наблюдения всегда дают отличное от нуля суммарное волновое поле.

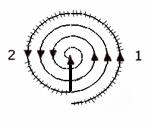
Рис. 6.10

Рис. 6.10 соответствует случаю, когда закрыты первая и вторая зоны Френеля. Волновое поле в точке наблюдения описывается вектором, соединяющим конец левой полуокружности второй зоны с центром спирали. Отсюда следует, что при наличии такого диска волновое поле в точке наблюдения по сравнению с волновым полем в отсутствие диска имеет несколько меньшую амплитуду и такую же фазу (сравниваемые векторы имеют одинаковую ориентацию). С увеличением числа закрытых зон Френеля начало изображающего вектора скользит по спирали, а его конец остается неподвижным. Таким образом, амплитуда волнового поля в точке наблюдения с ростом числа закрытых зон Френеля монотонно уменьшается, всегда оставаясь отличной от нуля.

Опыт Араго показывает невозможность получения нулевого волнового поля с помощью круглого непрозрачного диска сколь угодно большого размера, если точка наблюдения лежит на оси симметрии. Однако практически равное нулю волновое поле легко получается посредством непрозрачного экрана с круглым отверстием, открывающим две первые зоны Френеля. В этом случае волновое поле описывается вектором очень малой длины, соединяющим начало правой полуокружности первой зоны с концом левой полуокружности второй зоны.

Осесимметричная дифракция эффективно используется в оптическом устройстве, которое называется зонной пластинкой. Зонная пластинка представляет собой плоскую непрозрачную пластинку, в которой для заданной точки наблюдения прорезаны только нечетные или только четные зоны Френеля. В результате все вторичные волны, приходящие в точку наблюдения, находятся в фазе и усиливают друг друга при интерференции. Таким образом, происходит фокусировка плоской монохроматической волны падающей на зонную пластинку. Особенность зонной пластинки заключается в том, что её можно использовать как фокусирующую (собирающую), так и дефокусирующую (рассеивающую) линзу. Следует отметить, что плоская технология является более простой, чем технология изготовления линз со сферической поверхностью. Кроме того, возможно создание зонных пластинок для волн различной физической природы, включая акустические волны и радиоволны.

Лекция №7

Дифракция Фраунгофера

1. Приближения геометрической оптики, Френеля и Фраунгофера.