дифракционная решётка

Рис.8.1

Примером оптического спектрального прибора может служить дифракционная решётка, работающая на пропускание. Данная дифракционная решётка представляет собой непрозрачный плоский экран, в котором на одинаковом расстоянии d прорезано большое число N одинаковых параллельный щелей шириной b. Расстояние d называется периодом решётки и удовлетворяет условию

d>b>>λср, (8.6)

где λср – средняя длина волны исследуемого излучения. Величины d,b и N являются основными параметрами дифракционной решётки. Полная ширина дифракционной решетки .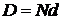

Пусть на решётку нормально падает плоская монохроматическая волна

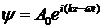, (8.7)

где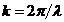, 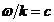и -постоянная амплитуда волны. Волна частично проходит через щели, испытывая дифракцию. Многолучевая интерференция дифрагированных волн наблюдается на экране, который параллелен плоскости решётки и находится на расстоянии L от решётки в дальней зоне дифракции, где волновой параметр 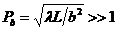и справедливо приближение Фраунгофера (рис.8.2).

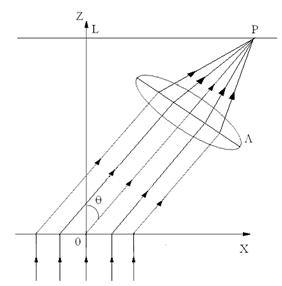
Рис.8.2

Дифрагированные волны, идущие от N щелей, фокусируются в точку наблюдения Р с помощью собирающей линзы L. Точка наблюдения Р задается углом 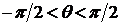между осью z, проходящей через центр решётки, и направлением на эту точку из центра решётки х=0. Угол θ считается положительным, если точка P находится в области x>0, и считается отрицательным, если точка P находится в области x<0.

Волновое поле на поверхности каждой щели рассматривается как вспомогательный источник вторичной волны с интенсивностью в дальней волновой зоне

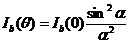, (8.9)

где 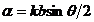, — максимальная интенсивность дифрагированной волны, идущей от одной щели в направлении нормали к плоскости решетки ().

Разность фаз двух параллельных дифрагированных волн, идущих от соседних щелей под углом, описывается формулой

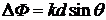, (8.10)

поэтому полное волновое поле в точке наблюдения Р получается путём сложения всех вторичных волн, идущих от N щелей,

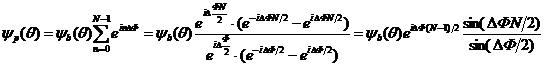. (8.11)

Здесь — волновое поле, созданное излучением от щели с наименьшим расстоянием до плоскости собирающей линзы. В (8.11) использована формула для суммы ряда, члены которого образуют геометрическую прогрессию.

Соответствующая интенсивность с учетом (8.9) определяется выражением

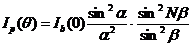, (8.12)

где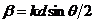. Это угловое распределение интенсивности света, прошедшего через решетку, практически наблюдается только в пределах угловой ширины центрального дифракционного максимума 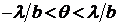одной щели и имеет главные максимумы, побочные максимумы и минимумы.

Главные интерференционные максимумы (спектры), где интенсивность

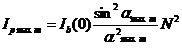, (8.13)

наблюдаются для углов удовлетворяющих уравнению

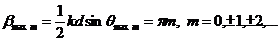(8.14)

или

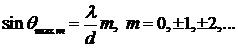. (8.15)

Здесь m – порядок спектра. При выполнении условия (8.15) дифрагированные волны от всех щелей приходят в точку наблюдения в фазе и возникает усиливающая интерференция.

Минимумы интенсивности, где

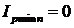, (8.16)

наблюдаются при , удовлетворяющих уравнению

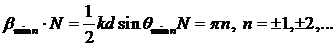(8.17)

причем n≠±N, ±2N,… или

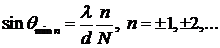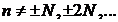; . (8.18)

Здесь n-порядок минимума. Между двумя соседними главными максимумами находиться N-1 минимум.

Анализ выражения (8.12) показывает, что между двумя соседними минимумами интенсивности находится один побочный максимум с такой малой интенсивностью, что эти побочные максимумы практически не видны. Между двумя соседними главными максимумами всего находится N-2 побочных максимума.

График зависимости от приведен на рис 8.3. «Тонкая» структура этого распределения определяется многолучевой интерференцией дифрагированных волн, а «грубая» структура в виде огибающей главных максимумов — дифракцией на отдельной щели.

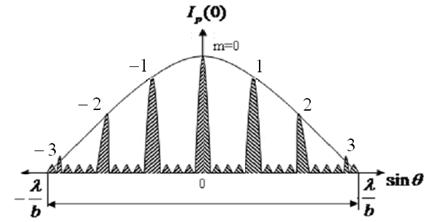
Рис.8.3

Угловая ширина главных максимумов по определению равна разности углов для двух ближайших минимумов слева и справа от главного максимума. Согласно уравнению (8.18) при условии |θ|<<1 и 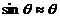угловая ширина равна

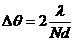(8.19)

и уменьшается с ростом числа щелей как 1/N.

В соответствии с приближением Фраунгофера распределение волнового поля в дальней зоне есть фурье-образ волнового поля на плоскости сразу за дифракционной решёткой. Важнейшей особенностью этого нового распределения волнового поля заключается в том, что пространственное положение главных максимумов (спектров) с m≠0 зависит от длины волны λ и соответственно частоты 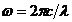падающей на решетку плоской монохроматической волны.