Сложение колебаний разной частоты

Задача 2. Плоская электромагнитная волна падает на экран со щелью. На расстоянии 20 см от центра нулевого максимума находится центр первого дифракционного максимума освещенности экрана, расположенного на расстоянии 50 см от щели. Чему равна ширина щели, если длина волны равна 1 см?

Задача 3. Тонкий луч перпендикулярно проходит сквозь дифракционную решетку и, расщепившись, падает на экран. На сколько надо повернуть решетку вокруг оси, перпендикулярной лучу, чтобы расстояние между дифракционными максимумами увеличилось в два раза?

Задача 4. Кольцевой слой из диэлектрика с показателем преломления n перекрывает вторую зону Френеля (для длины волны l) для точки P. При увеличении толщины слоя до величины h освещенность в этой точке достигла максимальной. Как надо изменить показатель преломления слоя, чтобы при удвоении его толщины освещенность в точке P не изменилась?

занятие 1.3.3

спектры радиоволн

2. Сложение колебаний разной частоты

2.1 Колебания связанных осцилляторов

2.1.1 Знакомство с явлением

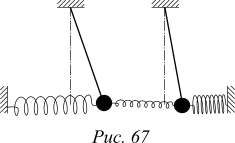Опыт 1. Два одинаковых маятника соединены слабой упругой связью. Если первоначально возбудить колебания только одного маятника, то постепенно колебания передаются другому, причем первый маятник на какое-то время даже останавливается. Потом второй маятник передает колебания первому.

Графики зависимости отклонений маятников от времени выглядят так, как показано на рисунке 66 предыдущего занятия. Огибающая колебаний первого маятника представляет собой график косинуса, а огибающая колебаний второго — график синуса. Оба маятника совершают модулированные колебания.

2.1.2 Моды связанных осцилляторов

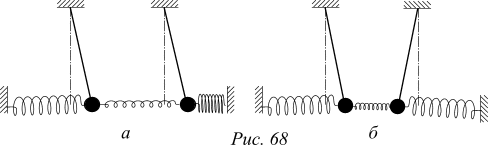Опыт 2. Те же связанные маятники возбуждаются иначе: в одном случае первоначальные отклонения маятников одинаковы (симметричный тип колебаний); в другом — первоначальные отклонения равны, но противоположны по фазе (антисимметричный тип колебаний, см. рисунки 68а и 68б).

Колебания, совершаемые в этих двух случаях, оказываются простыми гармоническими. Никаких биений нет.

Задача 1. Длины маятников в демонстрационных опытах, рассмотренных выше, равны L, массы грузов — m. Все три пружины одинаковы. Жесткости равны k. Найдите частоты колебаний, изображенных на рисунках 68а и 68б. Проведите качественные физические рассуждения, объясняющие, почему колебания маятников в противофазе происходят с большей частотой, чем колебания в фазе. Изменение: полагая, что g/L>>k/m, найдите разность частот.
Указание: в уравнениях движения маятников полагайте, что в любой момент при совершении колебаний типа 68а углы отклонения маятников равны между собой, а при совершении колебаний типа 68б имеют противоположные знаки.

Типы простых гармонических колебаний системы связанных маятников называются нормальными модами или просто модами. Каждая из мод имеет свою собственную частоту. Любая система упруго связанных осцилляторов может колебаться в той или иной моде.

Вопрос 1. Маятники из рассмотренных опытов колеблются не вдоль, а поперек пружин. Что собой представляют моды связанных маятников в этом случае?

Представления о модах удобны тем, что любое как угодно сложное движение системы упруго связанных осцилляторов представляет собой суперпозицию (наложение) мод. Так, например, отклонение первого маятника j1(t) в опыте 1 представляет собой сумму отклонений первого маятника системы, колеблющейся в первой моде и колеблющейся во второй моде: отклонение равно сумме отклонений мод

j1(t) = F01cos(w1t+ a1)+ F02cos(w2t+ a2), (1)
где F01 и F02 — “амплитуды” первой и второй мод, w1 и w2 — собственные частоты мод. Вначале, пока фазы обеих мод невелики, вклады в отклонение усиливают друг друга. Но, так как скорость нарастания фазы антисимметричной моды — w2 больше скорости нарастания фазы симметричной моды — w1, через некоторое время фаза высокочастотной моды опередит фазу низкочастотной моды на p. Вклады обеих мод в отклонение первого маятника будут взаимно уничтожать друг друга — первый маятник остановится. Зато амплитуда колебаний второго маятника станет максимальной. Когда разность фаз достигнет значения 2p, вклады опять будут усиливать друг друга и т. д.

Модулированное законом синуса колебание является наложением двух простых синусоидальных колебаний с мало отличающимися частотами.

Вопрос 2. Рассуждения о наложении мод применимы и для второго маятника. Почему же вначале, пока фазы мод значительно не изменились, вместо взаимного усиления вкладов в отклонение второго маятника имеет место ослабление?

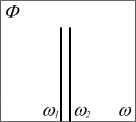Колебание, изображенное на рисунке 66 можно изобразить одной, более простой, картинкой — спектром колебаний (рисунок 69). Эта картина помимо простоты обладает еще одним преимуществом, по сравнению с рисунком 1: она содержит меньше деталей и более понятна. Но есть у нее и недостаток. Недостатком изображения колебаний в виде спектра является потеря информации о соотношении фаз складывающихся колебаний.

Пронаблюдайте моды тяжелой цепочки с одним свободным концом. Как связана частота колебаний цепочки с длиной волны возбужденной моды? Подумайте, как представить вращение цепочки в любой из устойчивых конфигураций в виде суперпозиции мод.

3*. Описание модулированных колебаний
методом векторных диаграмм

Колебание маятника в каждой из мод является простым синусоидальным, поэтому его можно изобразить с помощью вращающегося вектора. Рассмотрим с помощью метода векторных диаграмм результат наложения одинаковых вкладов мод вышерассмотренной системы двух маятников при нулевых значениях начальных фаз a1 и a2.

Вклад низкочастотной моды в отклонение маятника изобразится вектором, вращающимся с угловой скоростью 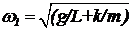. Вклад второй — высокочастотной моды — изобразится вектором, вращающимся с большей угловой скоростью По этой причине вектор высокочастотной моды будет все больше и больше обгонять вектор низкочастотной моды. Угол между векторами y со временем увеличивается по закону: y=w2t—w1t=(w2—w1)t. Таким образом, направления между векторами вкладов расходятся между собой и соответственно уменьшается амплитуда результирующего колебания.

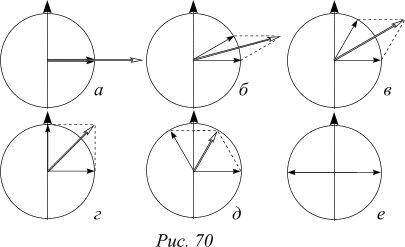Задание. Прокомментируйте последовательность рисунков, изображающих векторные диаграммы вкладов мод и результирующего от­клонения в различные последовательные моменты времени.

Задача 2. Систему из двух одинаковых маятников, описанных в задачах 1 и 2, возбудили следующим образом: удерживая маятник №2, отклонили маятник №1 на угол jо и затем оба отпустили.
а) Используя последовательность векторных диаграмм на рисунке 70, определите амплитуды возбужденных мод.
б) Из векторных диаграмм определите разность фаз мод в момент времени t (угол между векторами, изображающими колебания мод).
в) Из векторных диаграмм и геометрических соображений определите максимальное значение отклонения первого маятника (длину результирующего вектора) к моменту времени t.
г) Представляя движение маятника колебанием с медленно изменяющейся амплитудой по закону косинуса, определите частоты изменения амплитуды и колебаний маятника.
д) Запишите выражения зависимостей отклонений первого и второго маятников от времени.

Вопрос 3. Как будут выглядеть колебания маятников, если вклады мод имеют разные амплитуды? Как можно рассчитать зависимость амплитуды результирующего колебания от времени?

4. Спектральный состав радиоволн

4.1 Спектры радиосигналов

Любой периодический сигнал представляется суммой простых синусоидальных и косинусоидальных колебаний.

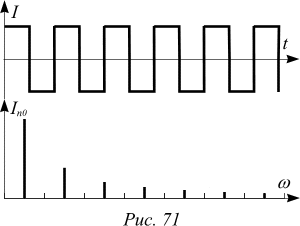Пример 1. Ток в электрической цепи представляет собой периодическую последовательность скачков (прямоугольный сигнал) с

периодом T. Оказывается, что такой закон изменения тока можно получить, сложив синусоиды с частотами 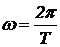, 3w, 5w, 7w и так далее. Амплитуды смешиваемых синусоид должны относиться друг к другу как последовательность чисел, обратных нечетным целым числам: 1, , , , … , … 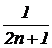и т. д.