Список заданий по сопротивлению материалов

СОДЕРЖАНИЕ

Предисловие………………………………………………………………………4

1. Расчётно-графическая работа №1 «Расчёты на растяжение-сжатие чугунных стержней»……………………………………………………………..5

2. Расчётно-графическая работа №2 «Расчёты на растяжение-сжатие стержней»………………….……………………………………………….……..10

Вопросы для защиты расчётно-графических работ №1, 2……………………15

3. Расчётно-графическая работа №3 «Геометрические характеристики плоских сечений»………………………………………………………………..15

Вопросы для защиты расчётно-графической работы №3……………………..22

4. Расчётно-графическая работа №4 «Расчёты на прочность и жёсткость при кручении»………………………………………………….…….……………….22

Вопросы для защиты расчётно-графической работы №4…………………….24

5. Расчётно-графическая работа №5 «Расчёты на прочность при изгибе»……………………………………………………………………………26

Вопросы для защиты расчётно-графической работы №5…………………….32

6. Приложение 1: «Некоторые механические свойства конструкционных материалов»……………………………………………………………………….33

7. Приложение 2: «Геометрические характеристики круглых поперечных сечений……………………………………………………………………………34

8. Приложение 3: «Тангенсы углов»……………………………………………35

9. Приложение 4: «Справочные данные для стандартных профилей проката (уголка, швеллера, двутавра)»…………………………………………………..38

10. Приложение 5: «Куб числа»……………………………………………………….55

11. Приложение 6: Основные формулы и зависимости «Сопротивления материалов»………………………………………………………………………61

12. Список литературы…………………………………………………………..62

ПРЕДИСЛОВИЕ

Сборник заданий по сопротивлению материалов предназначен для выполнения расчётно-графических работ последующим темам: «Растяжение-сжатие»; «Геометрические характеристики плоских сечений»; «Кручение»; «Изгиб».

В сборнике заданий содержатся таблицы с заданиями, расчётные схемы, вопросы для защиты расчётно-графических работ, механические характеристики материалов, таблицы тангенсов углов и корней кубических, справочные данные для стандартных профилей проката, основные формулы и зависимости по сопротивлению материалов.

Выполнение расчетно-графических работ из сборника является необходимым для повторения основных понятий теоретического материала, пройденного в лекциях по предмету: «Сопротивление материалов».

Расчётно-графическая работа №1.

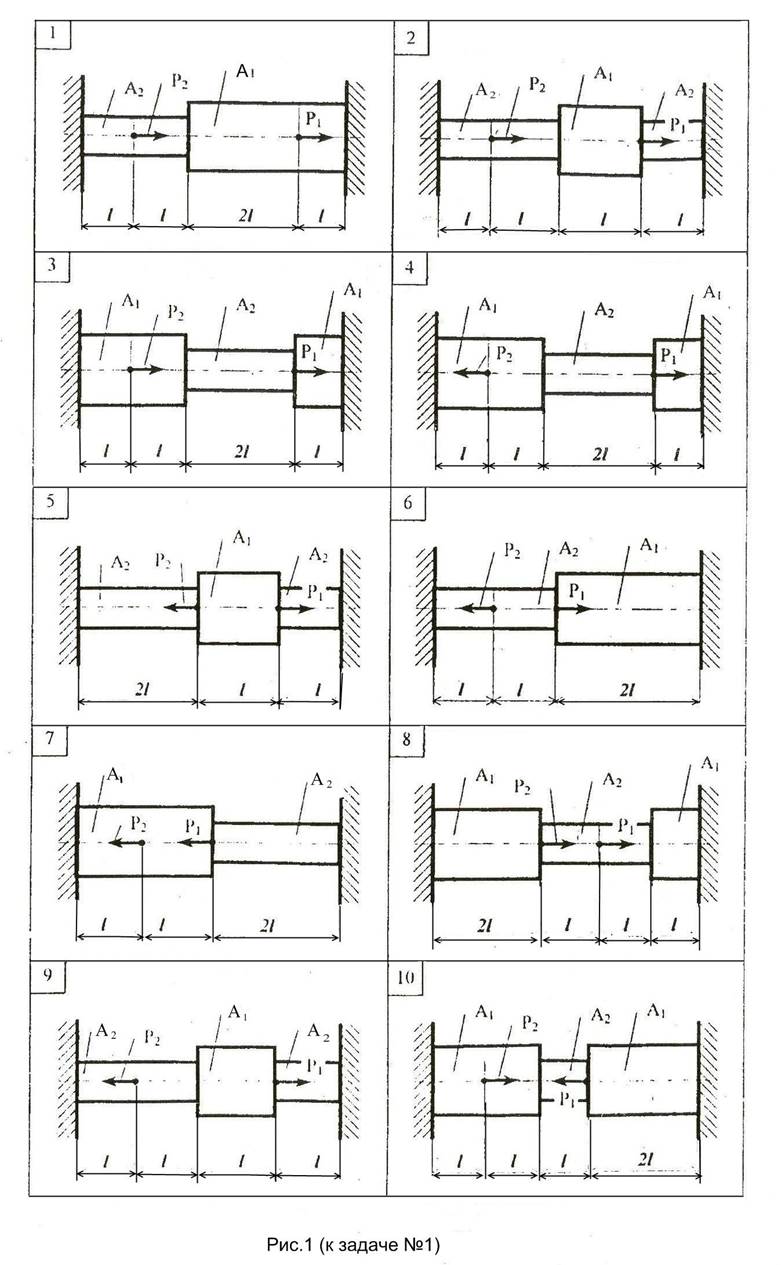
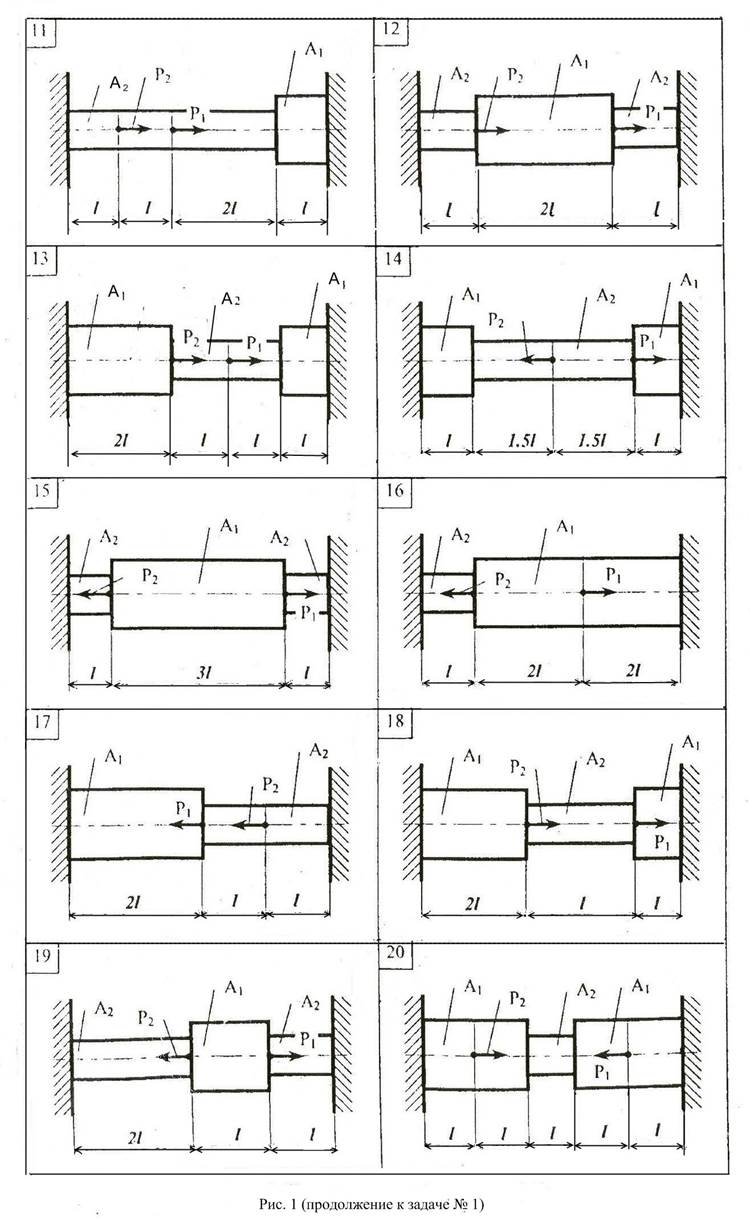
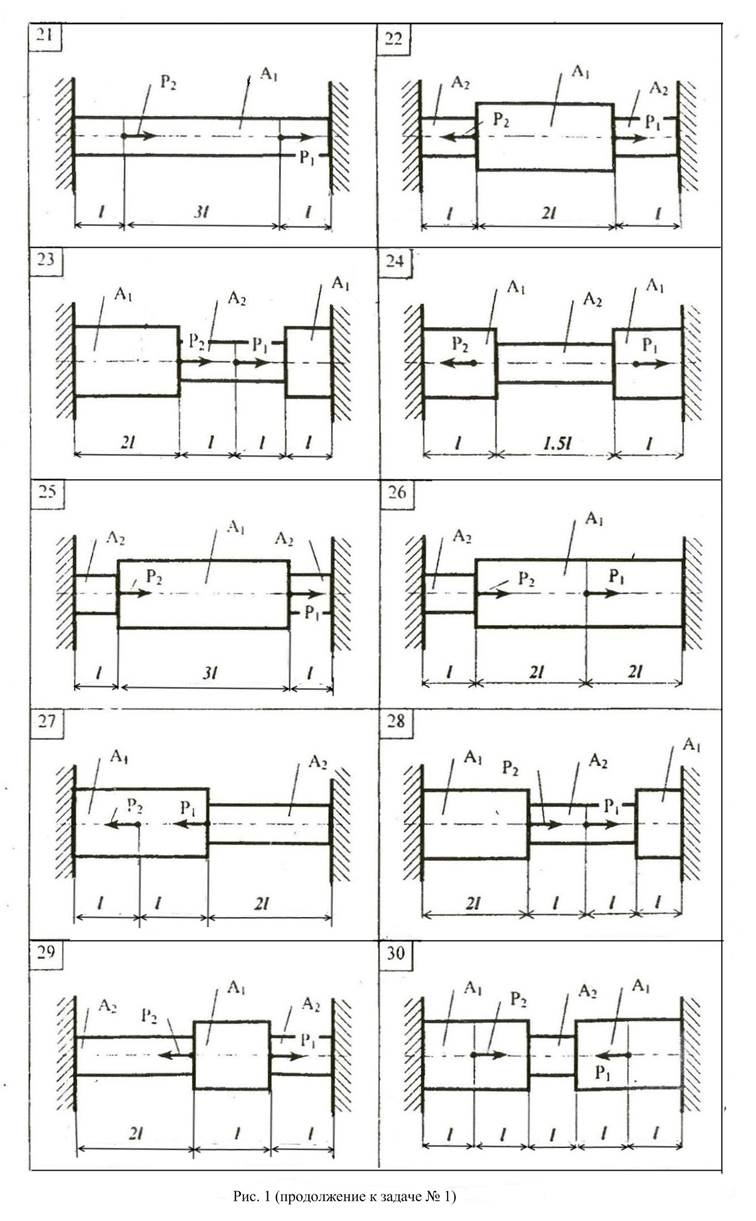
Расчеты на растяжение-сжатие чугунных cтержней.

Для заданного чугунного стержня:

1) Определить необходимые по условию прочности площади поперечных сечений стержней.

2) Определить перемещения сечений стержня (считая слева направо), относительно левой заделки.

Данные, необходимые для решения задачи, выбрать из таблицы вариантов (Табл.1). Механические свойства материалов стержней приведены в Приложении 1. При решении задачи модуль продольной упругости чугуна принять Е=120000 МПа. Коэффициент запаса прочности принять для всех вариантов принять n=2. Принять величину силы Р=50кН.

Указания к выполнению работы

1.  Определить степень статической неопределимости системы.

2.  Раскрыть статическую неопределимость системы, построить эпюры нормальной силы N, нормального напряжения σ и эпюру перемещений границ участков δ,

3.  Определить опасное сечение и из условия прочности подобрать размеры сечений стержней.

Таблица 1

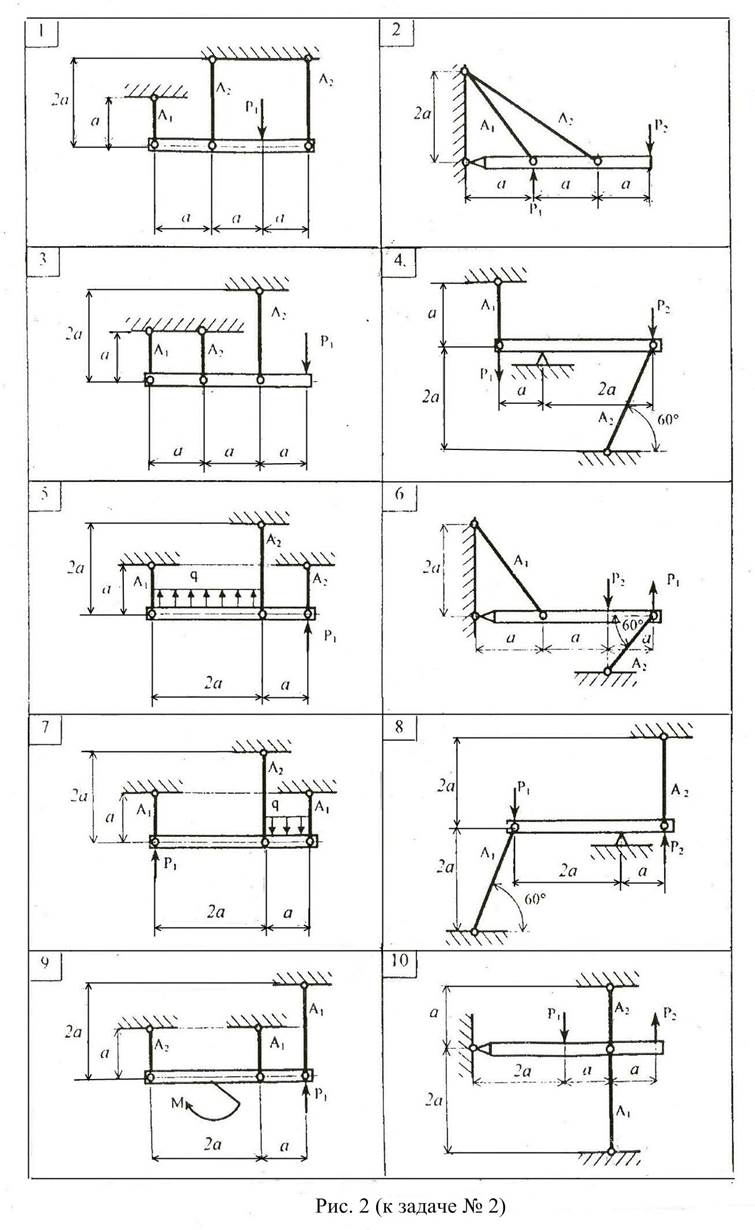
Расчётно-графическая работа №2.

Расчёты на растяжение-сжатие стержней.

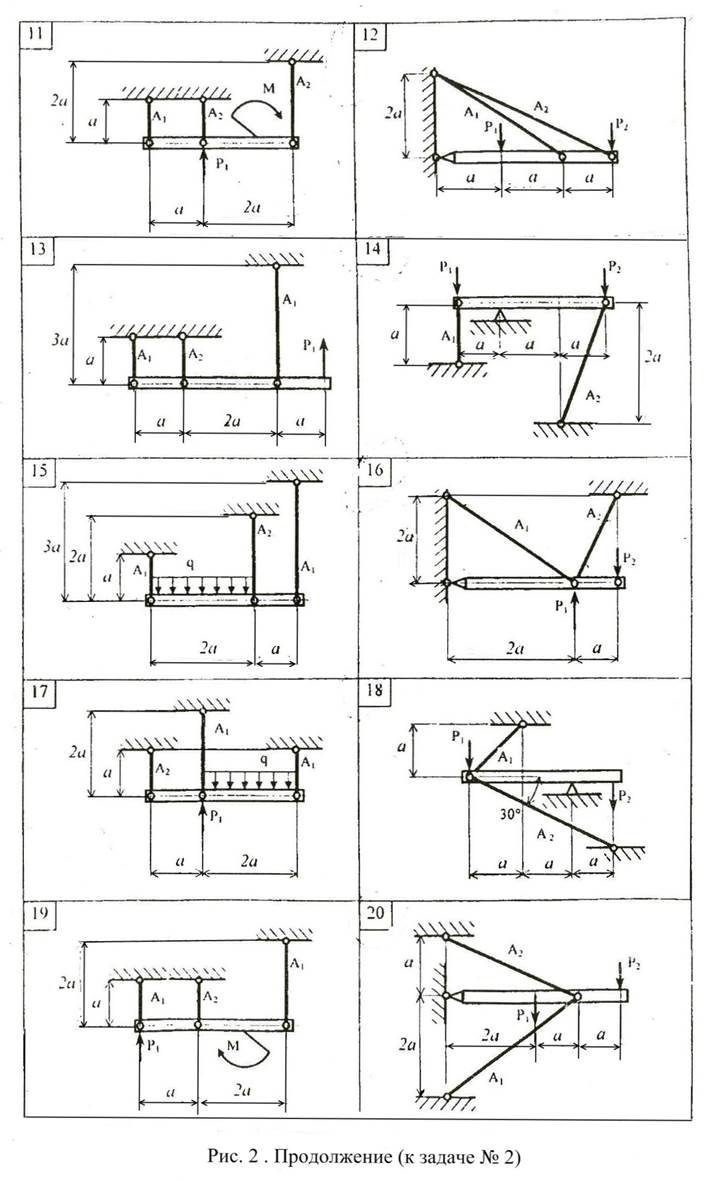
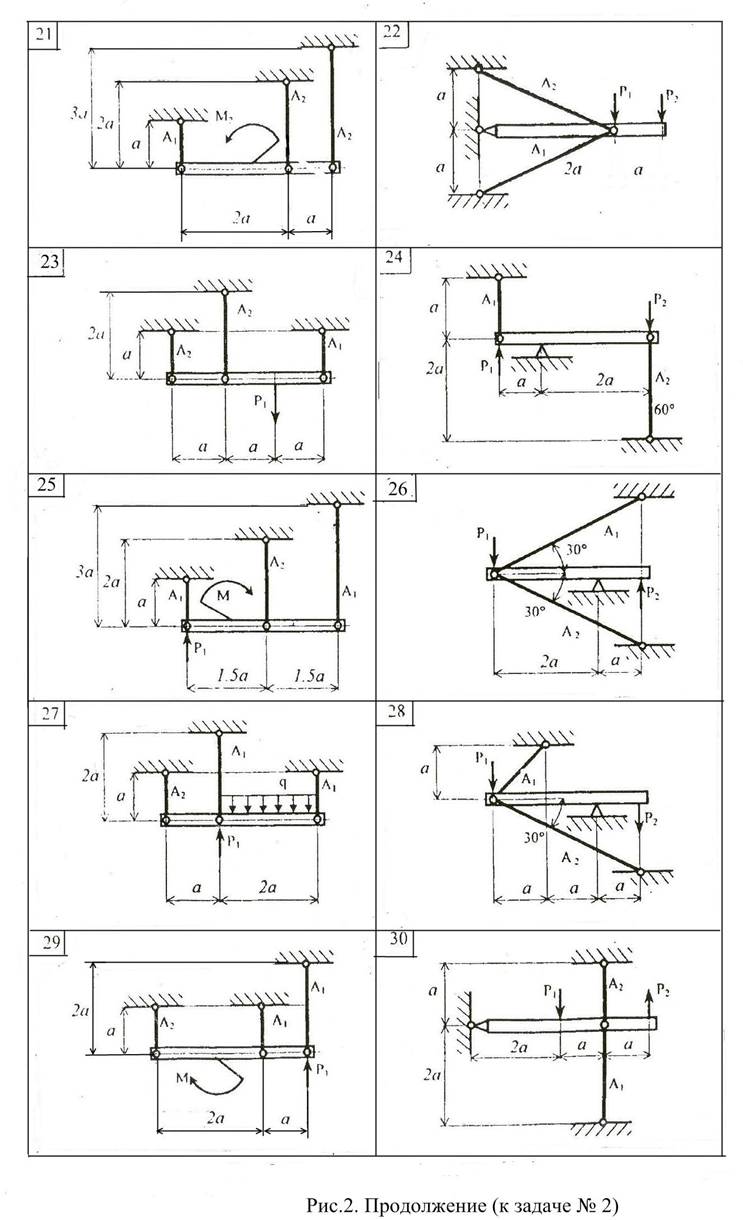
Абсолютно жесткий брус (рис.2) поддерживается стержнями и крепится посредством опорных устройств; к брусу приложена внешняя нагрузка. Для заданной конструкции требуется:

1. Определить из условия прочности площади поперечных сечений стержней

Данные, необходимые для решения задачи, выбрать из таблицы вариантов (Табл.2). При решении задачи модуль продольной упругости принять: для стали Е=200000 МПа; для чугуна Е=120000 МПа. Механические свойства материалов стержней приведены в Приложении 1. Коэффициент запаса прочности принять для всех вариантов: стальных стержней n=1,5; чугунных стержней n=2. Для вычисления силы Р принять размер а=500 мм, q=10 кН/м(там, где нет значения q в таблице).

Указания к выполнению работы

1. Определить степень статической неопределимости системы.

2. Раскрыть статическую неопределимость системы, выразив нормальные силы и нормальные напряжения в стержнях через параметр q.

Из условия прочности определить площади поперечных сечений. Устойчивость сжатых стержней считать обеспеченной.

Таблица 2

Вопросы для защиты расчетно-графических работ №1, 2

1. Что представляет собой расчётная схема и чем она отличается от реальной конструкции. В чем заключается сущность принципа Сен-Венана? 2. Какую деформацию бруса называют центральным растяжением или сжатием? Что называется нормальной (продольной силой) в нормальном сечении бруса, как ее вычисляют?

З. Что называется абсолютной и относительной продольной деформацией, их размерности?

4. Как формулируется закон Гука. Что называется модулем продольной
упругости, его физический смысл?

5. Сформулировать гипотезу плоских сечений. Как распределяются нормальные напряжения в поперечных сечениях стержня при растяжении-сжатии, как их вычисляют?

6. Что называется коэффициентом поперечной деформации, в каких пределах он изменяется для различных материалов?

7. Какие механические характеристики материала определяются пои испытаниях на растяжение и сжатие?

8. Сформулировать условие прочности. Что называется допускаемым напряжением, как его выбирают для пластичных и хрупких материалов.

9. Какие системы называются статически неопределимыми, как выявляют степень статической неопределимости?

10. Какие особенности характерны для статически неопределимых систем.
Какие напряжения называются монтажными, температурными.
11. Что положено в основу процедуры раскрытия статической

неопределимости системы?

12. Как вычисляют напряжения и наклонных площадках центрально растянутого стержня?

13. Как вычисляется потенциальная энергия упругой деформации при растяжении-сжатии стержня?

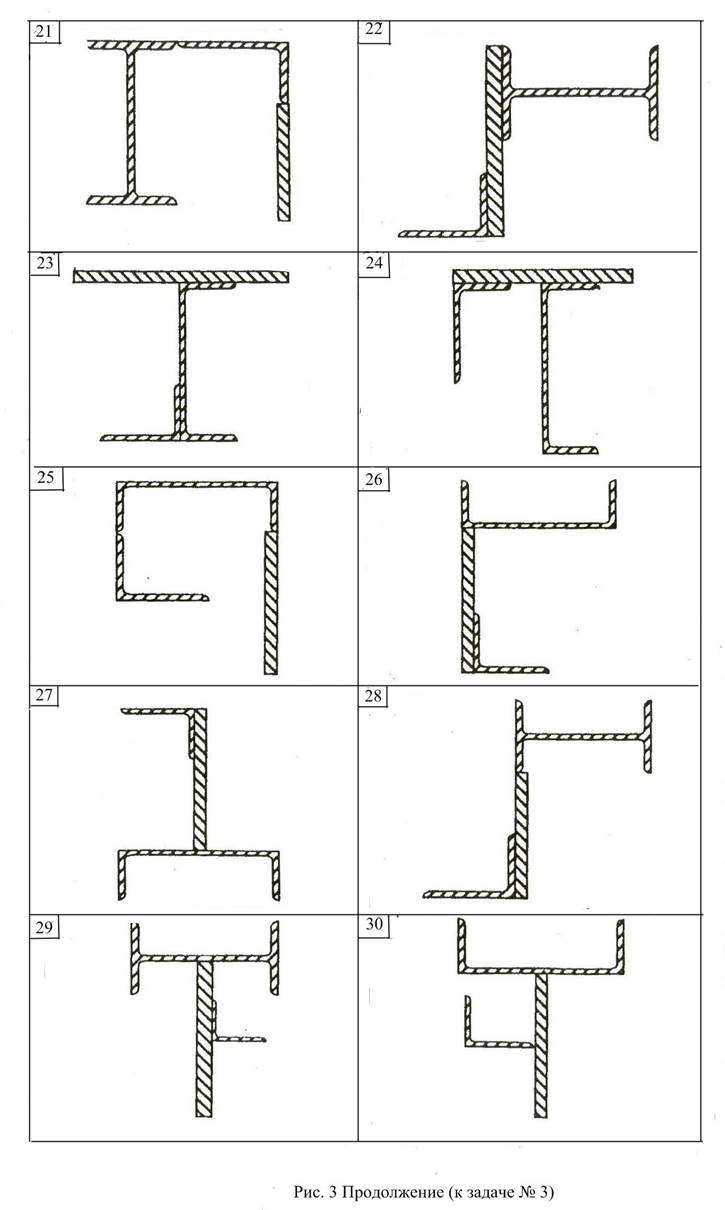
Расчётно-графическая работа №3: Геометрические характеристики плоских сечений.

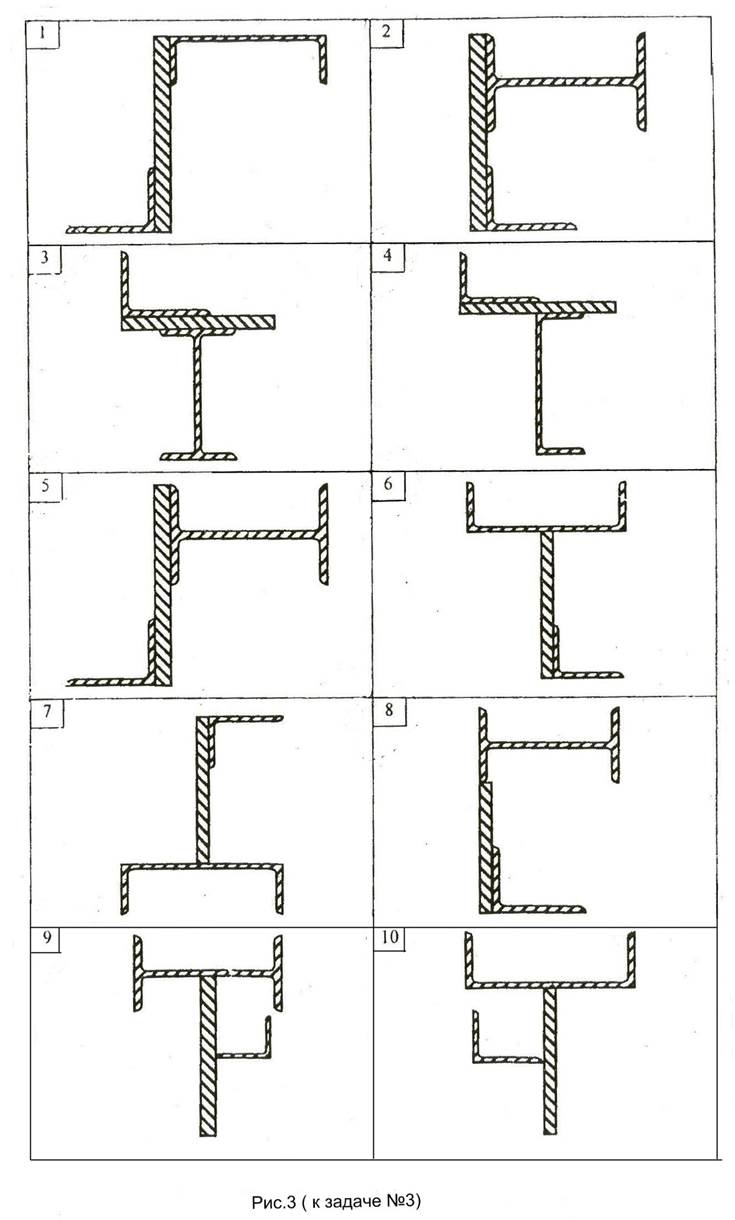
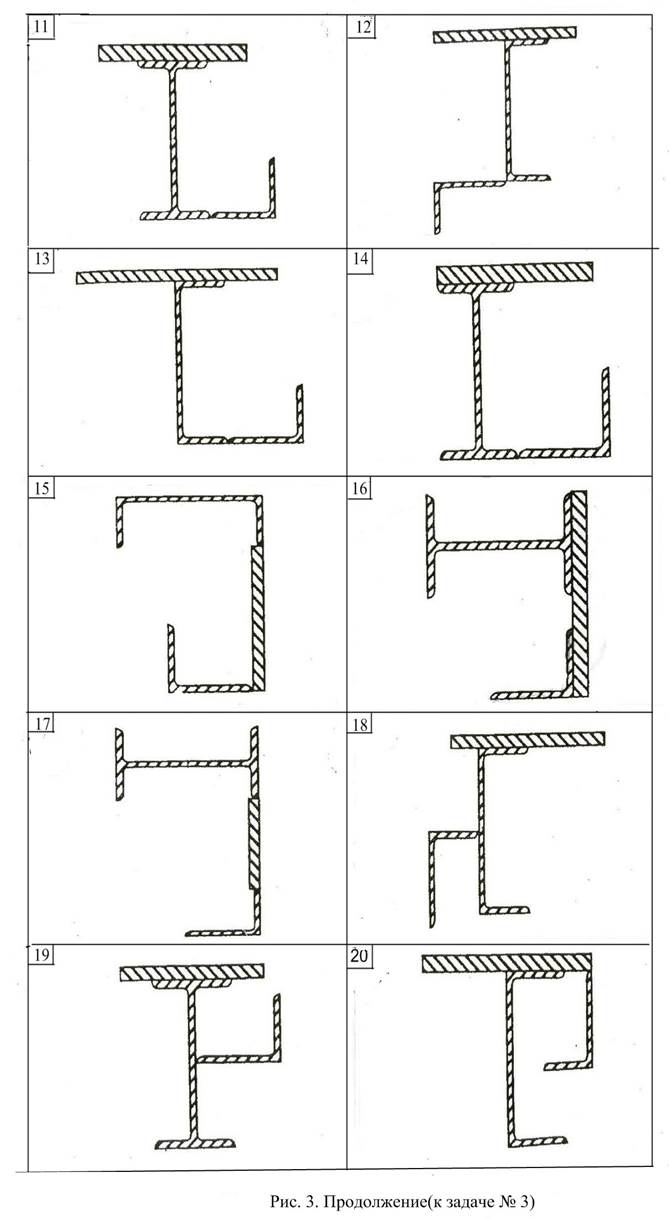
Для заданного сечения (рис.3), состоящего из трех фигур (прокатных профилей): уголка(№1); двутавра(№2) (или швеллера); полосы(№3) определить:

1. Положение главных центральных осей инерции.

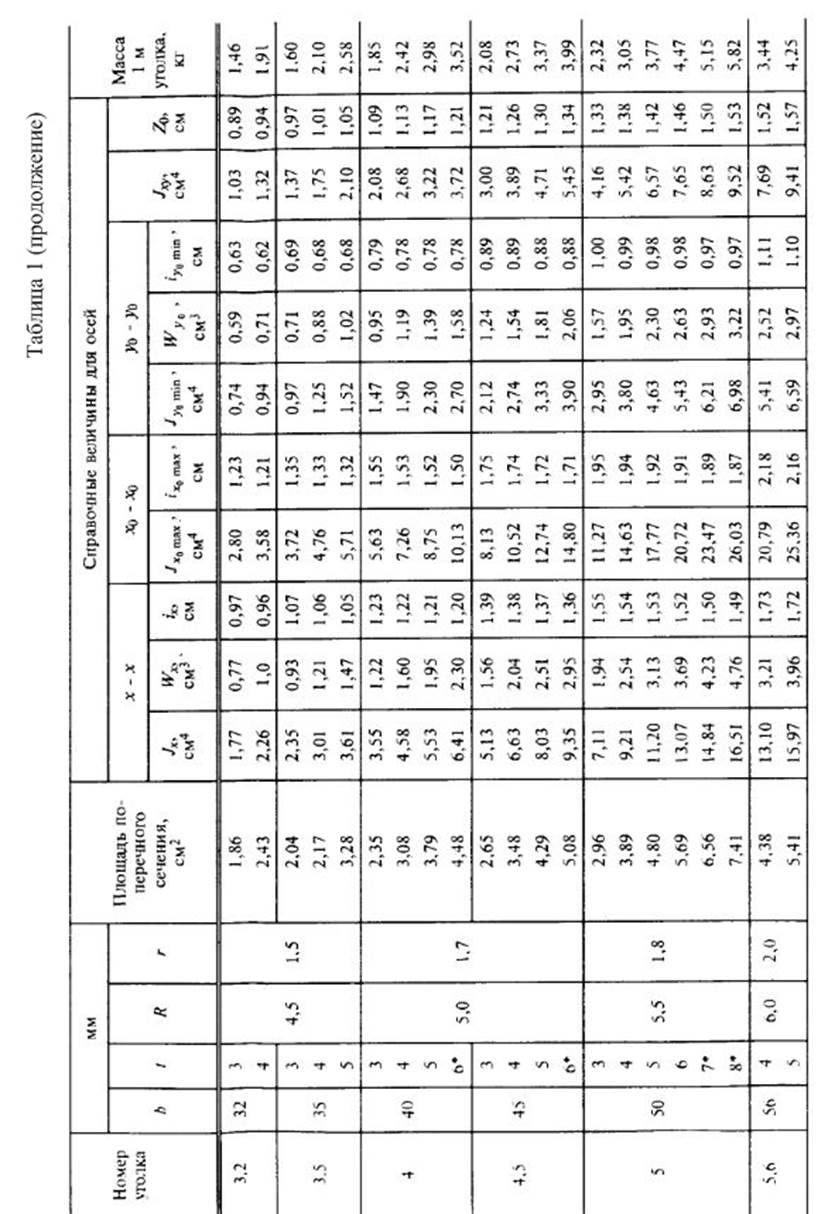
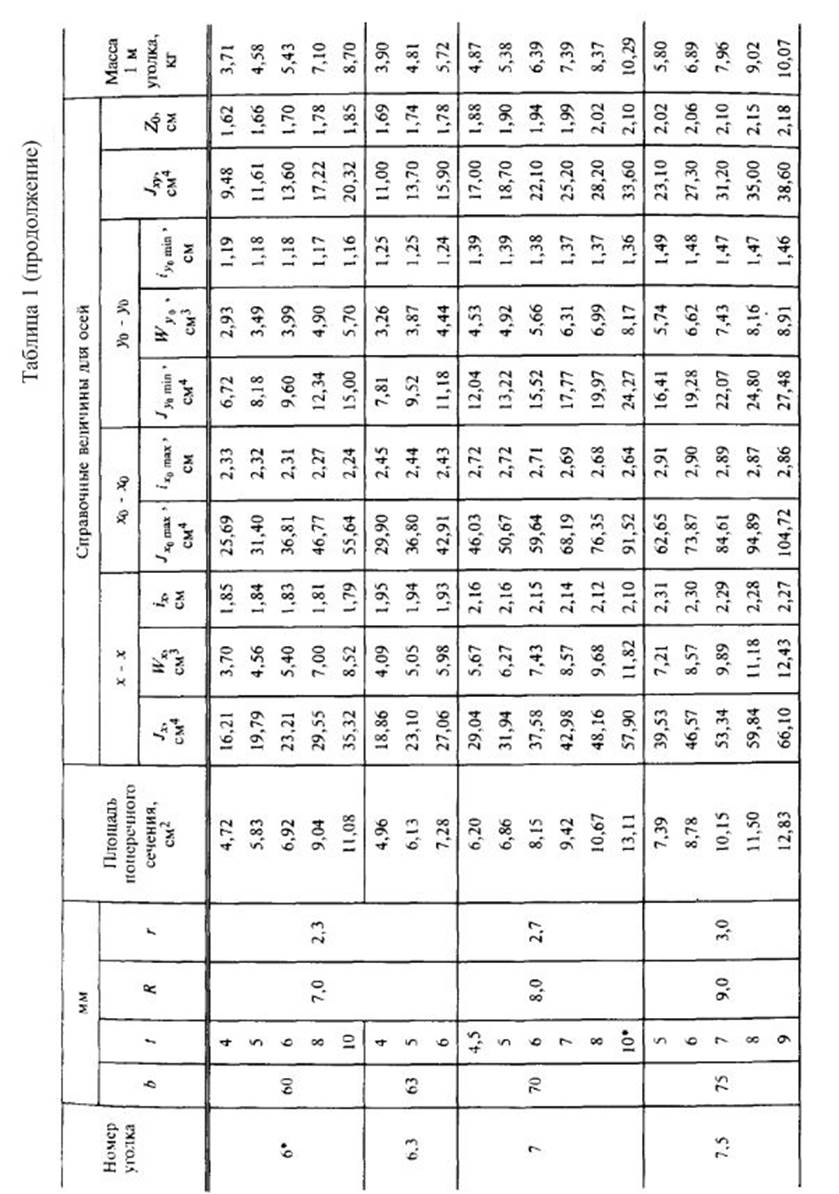
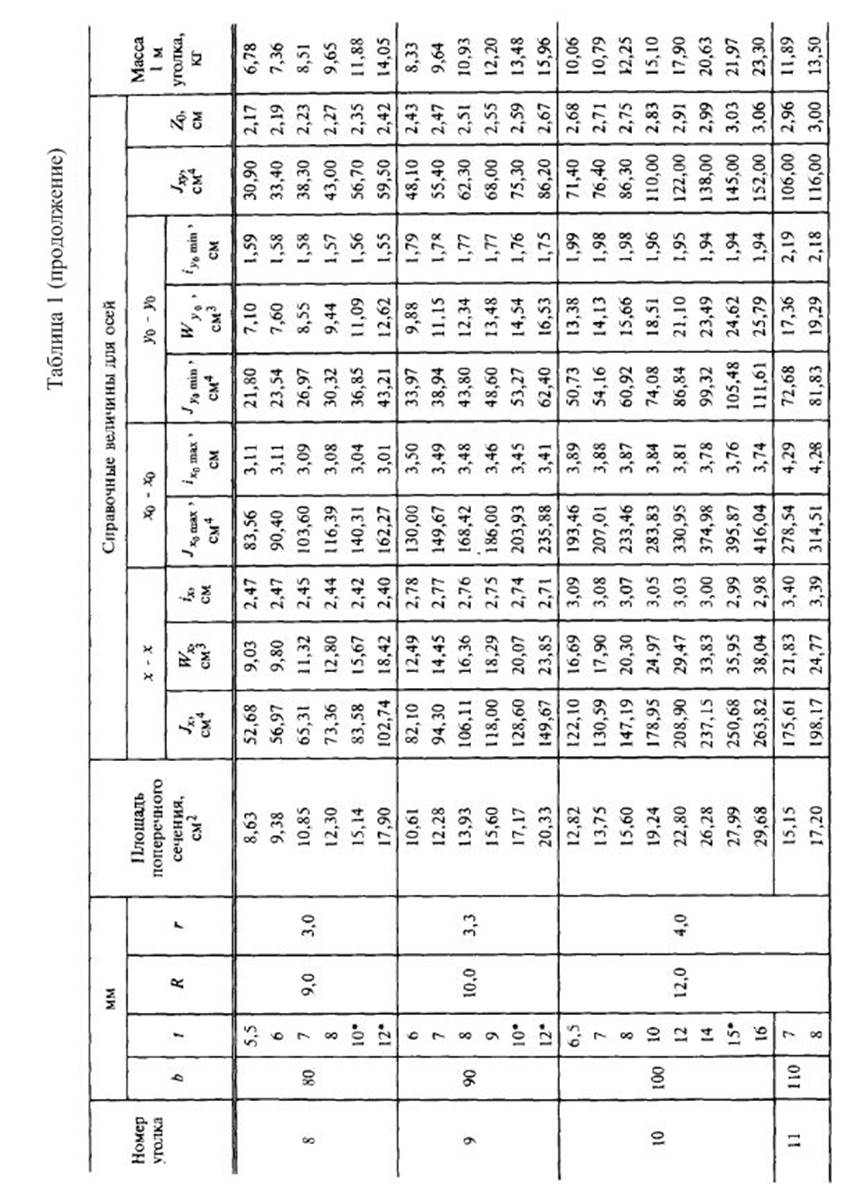
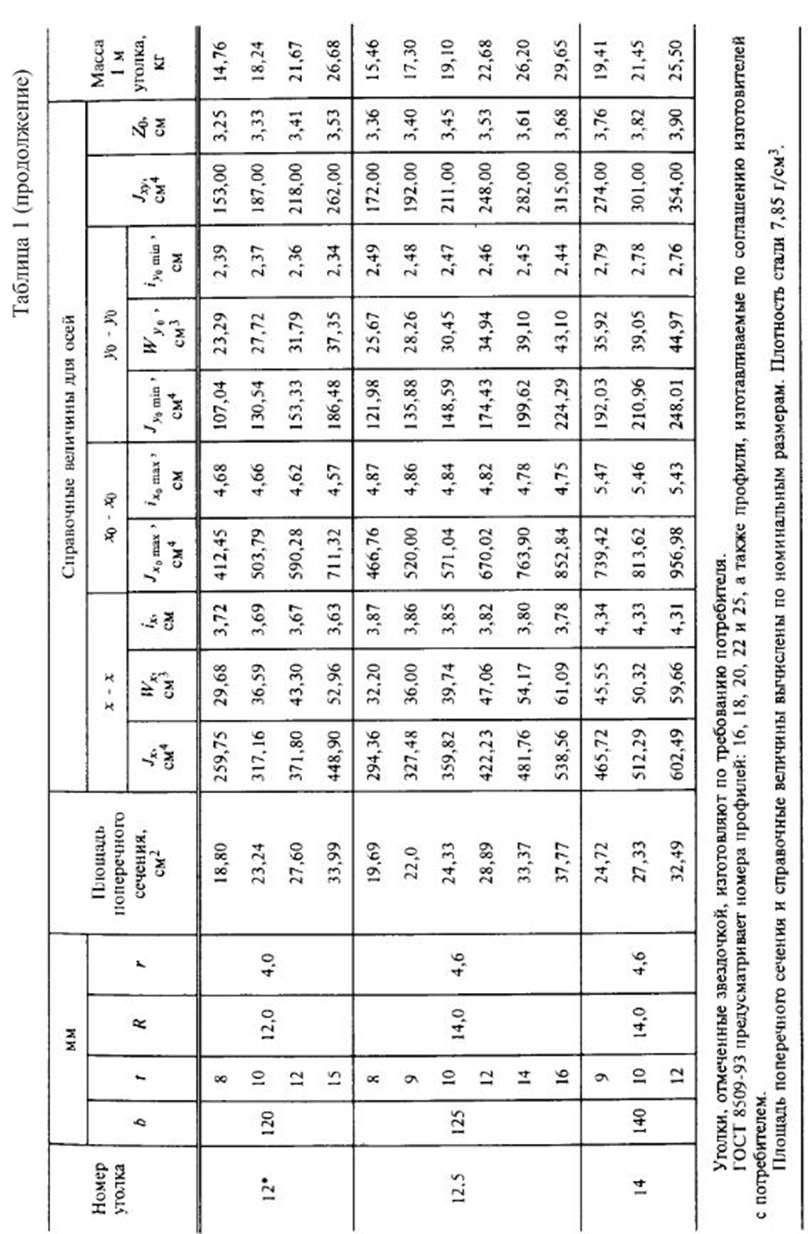
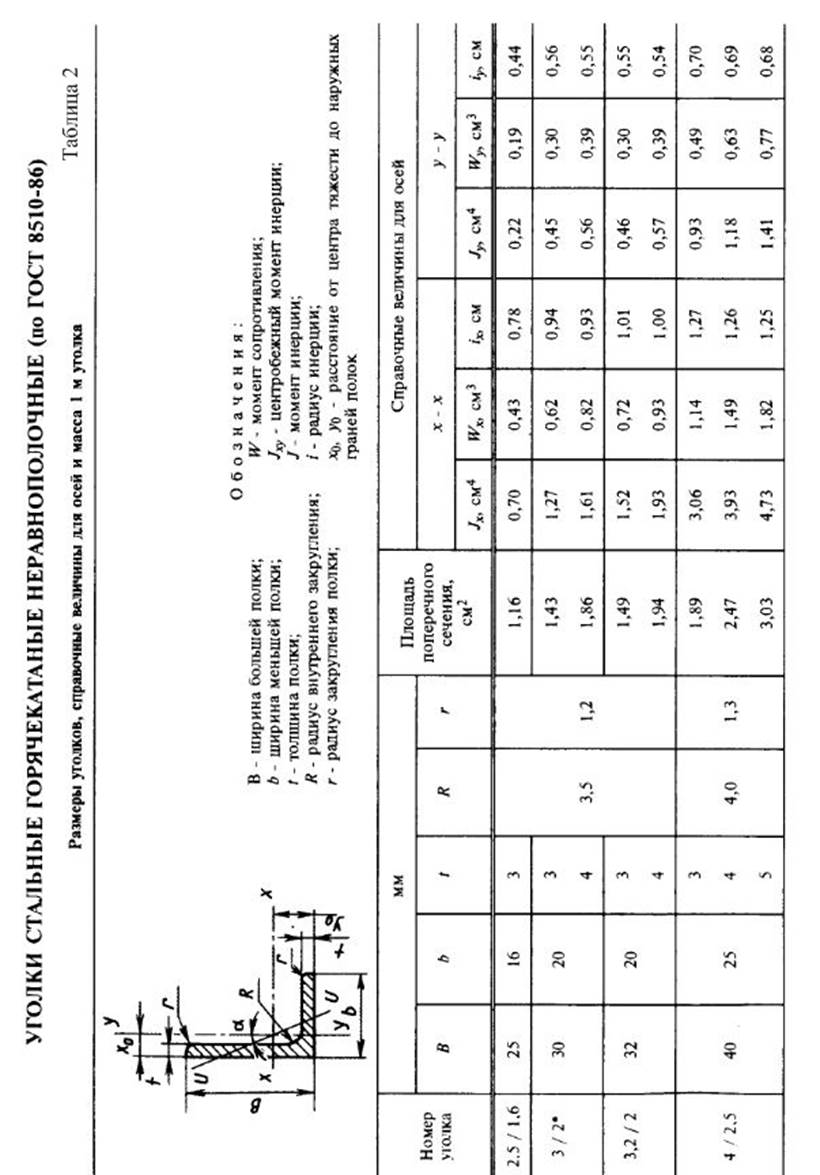
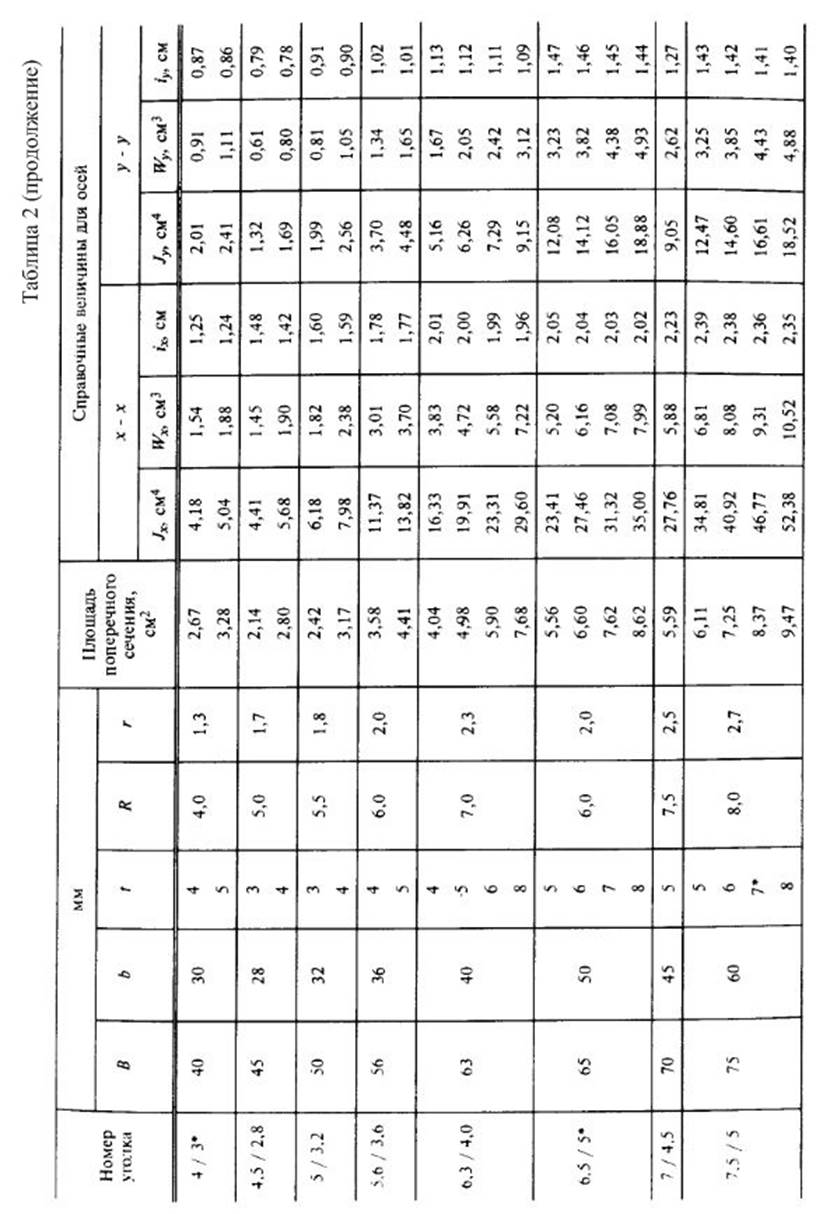
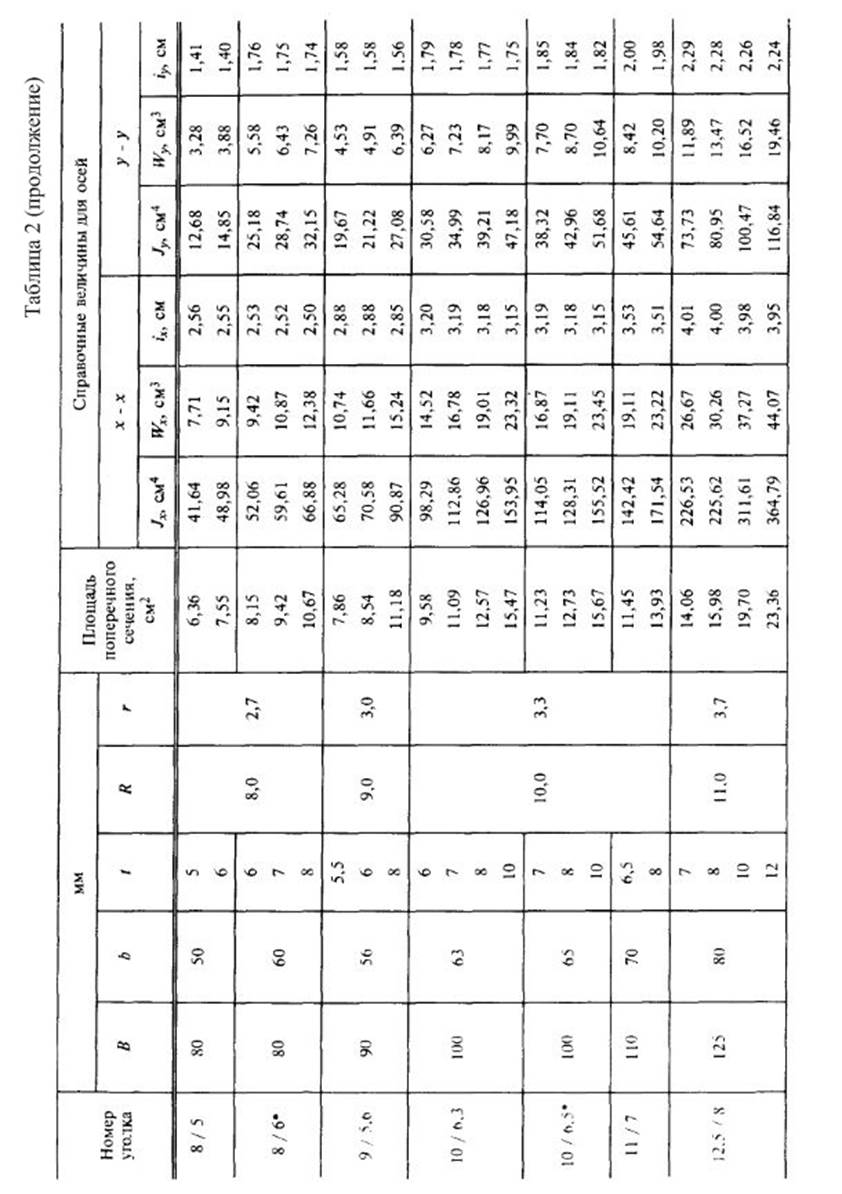
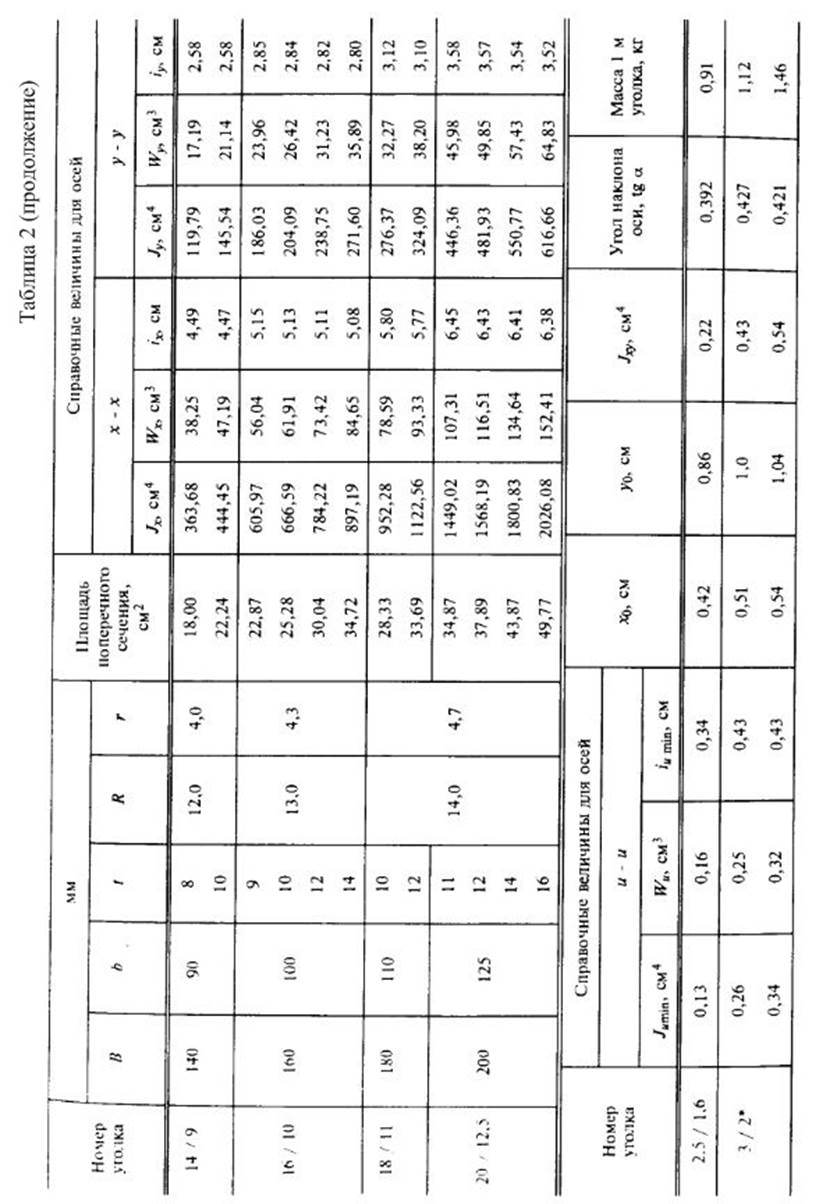
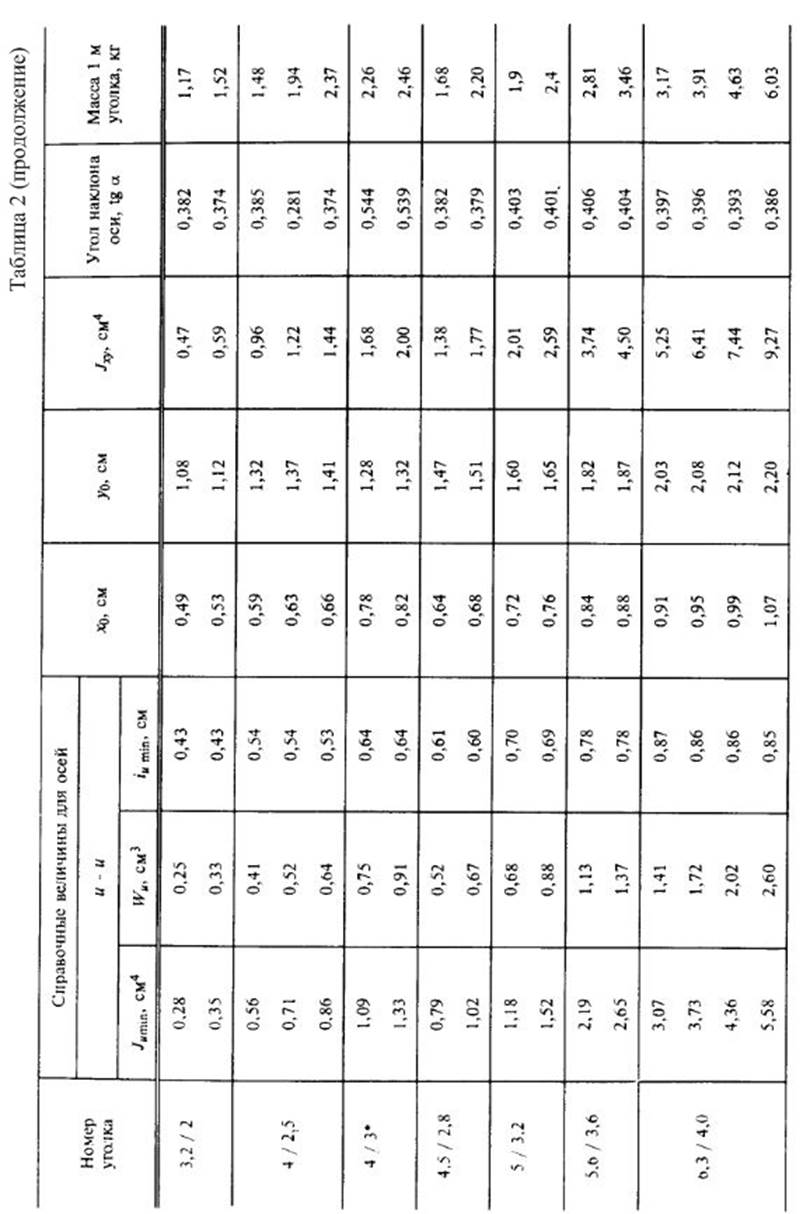
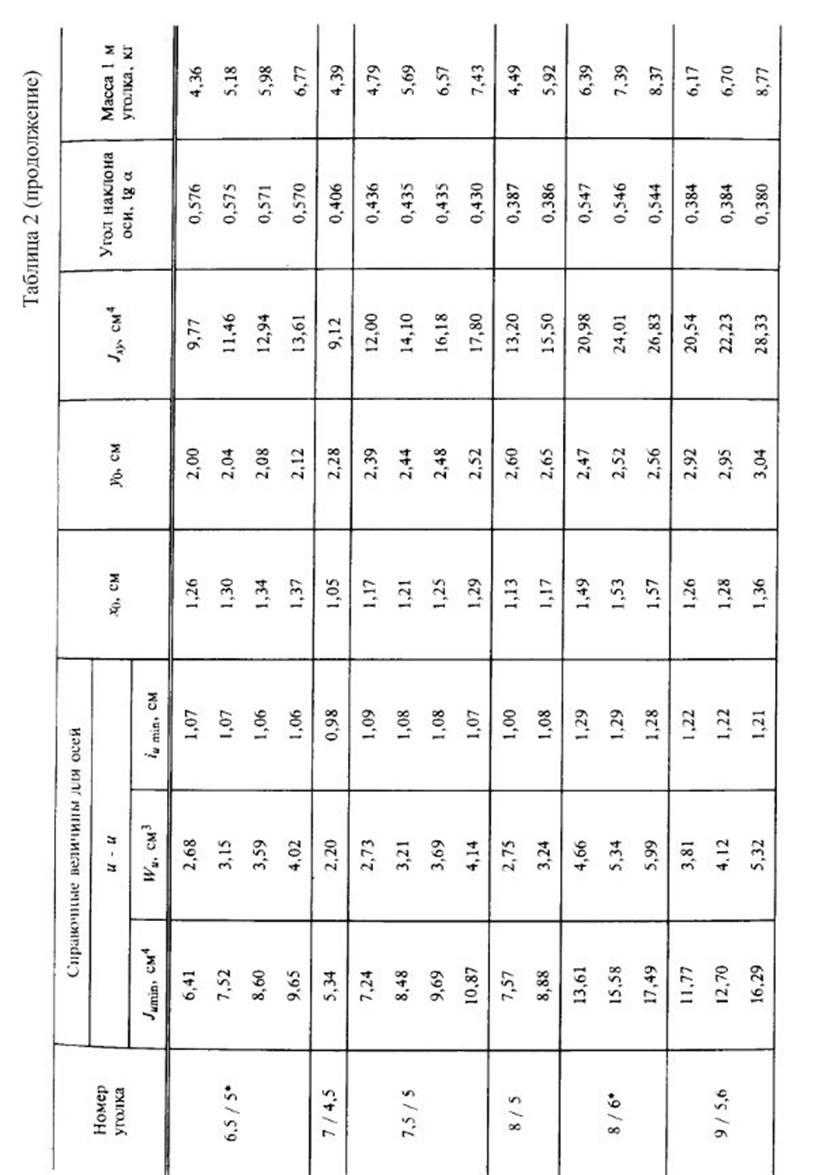
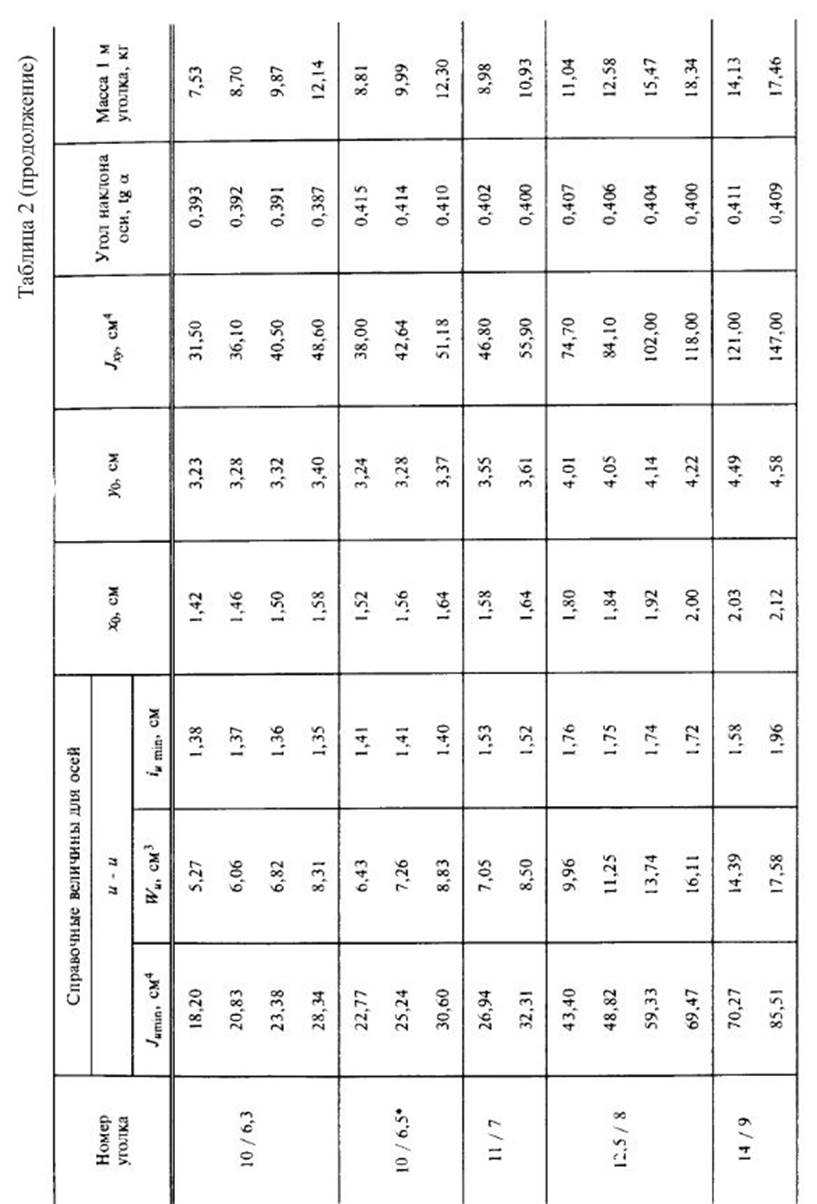
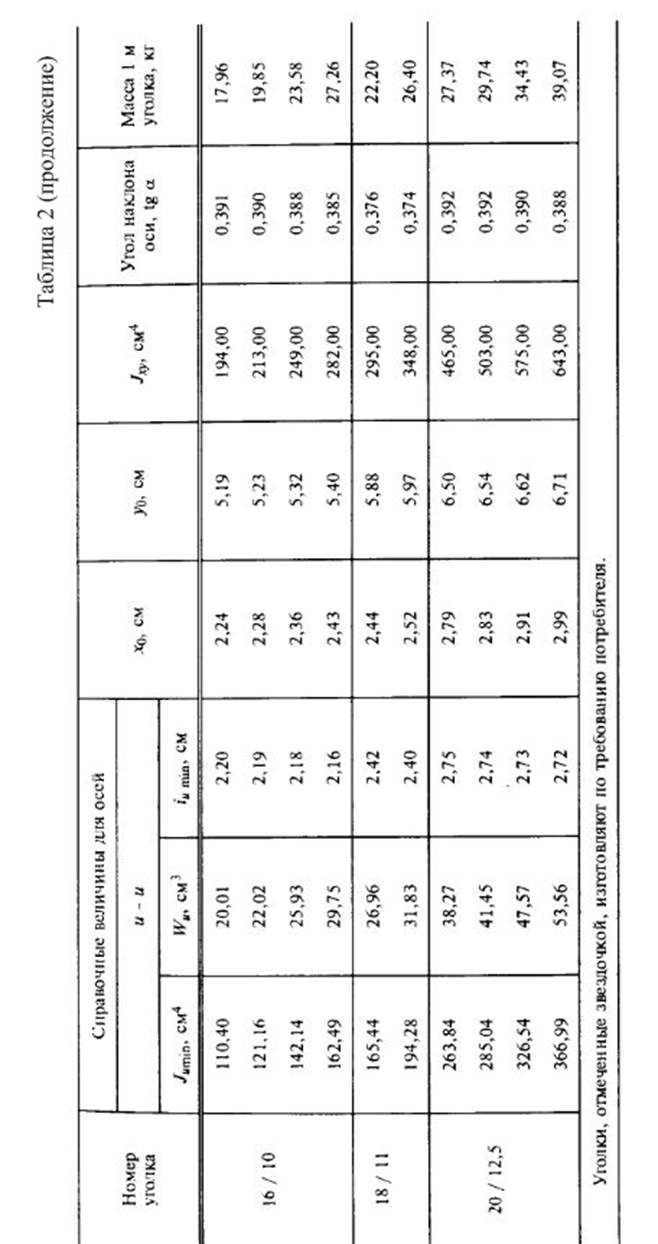
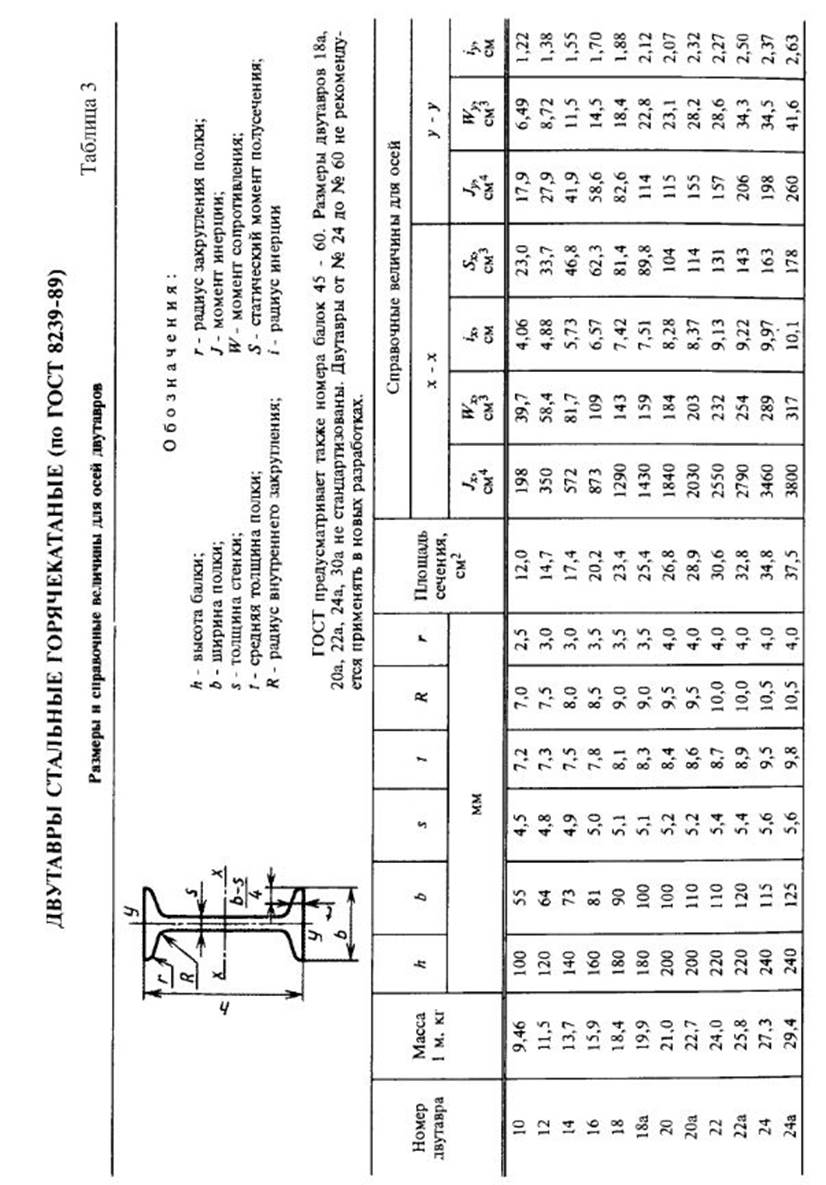
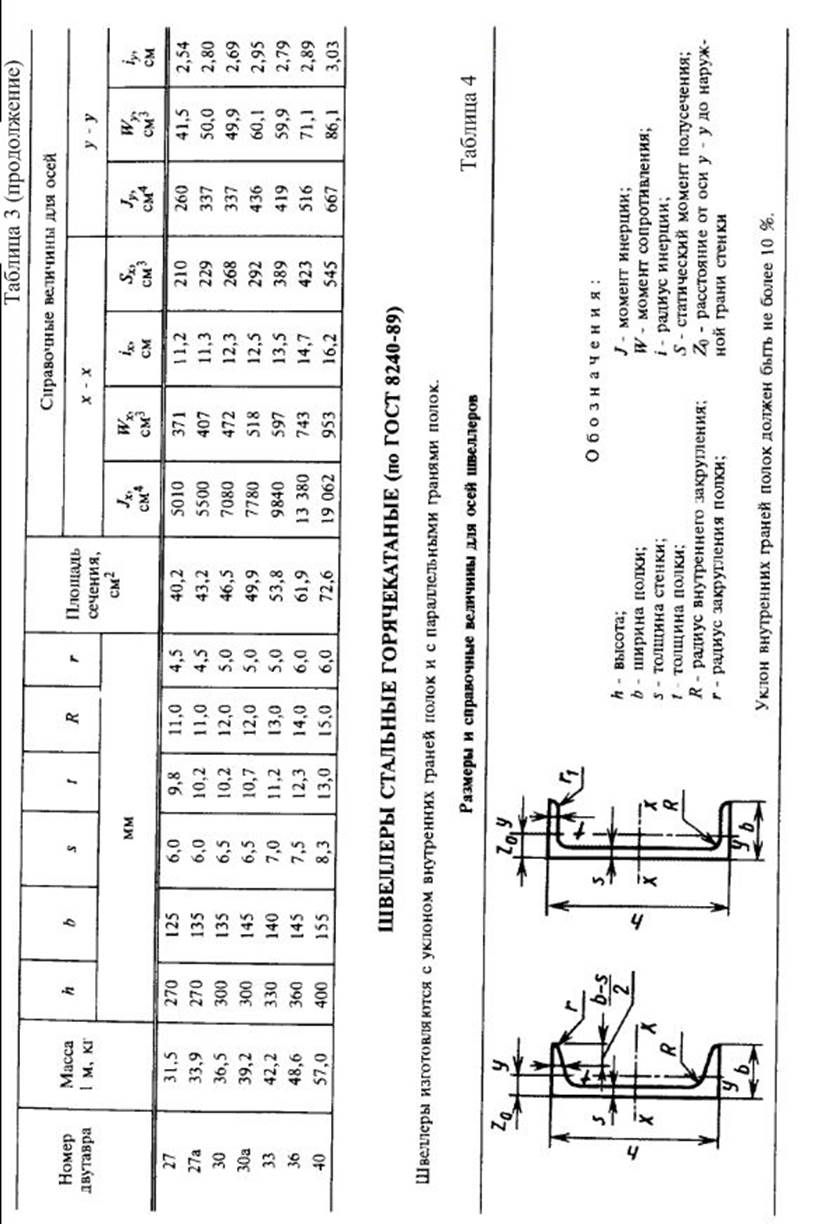
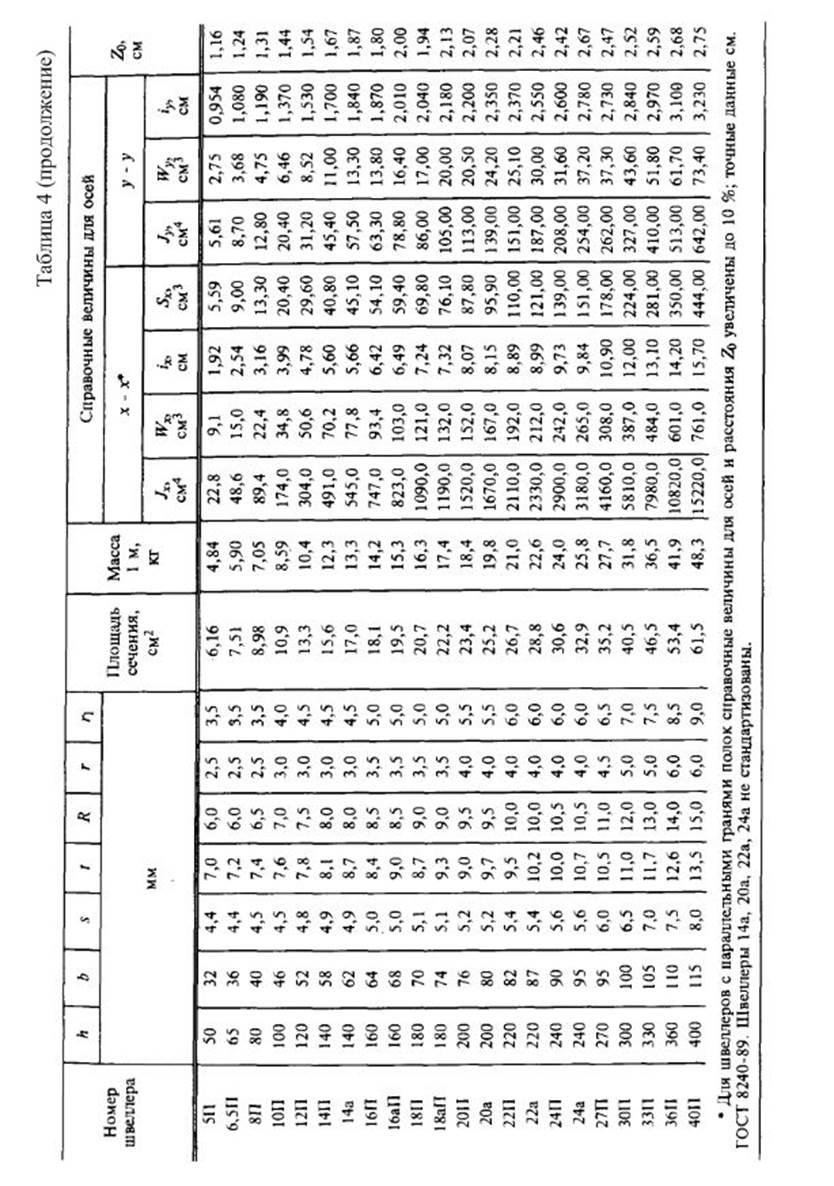
2.Вычислить главные центральные моменты инерции сечения. Данные, необходимые для решения задачи, выбрать из таблицы вариантов (Табл.3). Геометрические характеристики прокатных профилей можно найти в приложении 4 (таблицы с 1 по 4) сборника заданий по сопротивлению материалов или справочниках и учебниках по сопротивлению материалов, например в [1],[2],[3] из списка литературы.

Указания к выполнению работы

1. Заданное сечение вычерчивается в стандартном масштабе на листе формата A4.

2. На чертеже сечения показывается положение главных центральных осей. сечения.

3. На чертеже сечения обозначается также положение первоначальных осей, собственных центральных осей отдельных частей сечения, расстояния и углы между осями в общем и числовом виде.

4. Шаблон таблицы результатов приводится ниже (таблица 4), в неё должны быть сведены результаты вычислений.

Таблица 3

В скобках указана толщина полок уголка в мм.

Вопросы для защиты расчетно-графической работы №3

1. Что называется статическим моментом сечения относительно оси, какова его размерность.

2. Какова связь между статическими моментами относительно двух параллельных осей.

З. Чему равен статический момент относительно центральный оси.

4. Как определяются координаты центра тяжести простого и сложного сечений.

5. Что называется осевым, полярным и центробежным (смешанным) моментами инерции, какова их размерность и свойства.

6. Выведите формулы для определения осевых моментов инерции прямоугольника, треугольника и круга относительно центральных осей.

7. Чему равны полярные моменты инерции круга и кольца относительно центральных осей.

8. Какова зависимость между моментами инерции относительно параллельных осей, если одни из них центральные.

9. Как изменяются моменты инерции относительно центральных осей при их повороте.

10. Какие оси называются главными центральными осями инерции сечения. Какие осевые моменты инерции называются главными, каким свойством они обладают.

11 Чему равен центробежный момент относительно главных осей инерции.

12. Какие геометрические признаки сечения позволяют определять положение главных осей инерции.

13. Порядок вычисления главных моментов инерции сложного сечения.

14. Как изменяются значения моментов инерции правильных фигур (круг, квадрат равносторонний треугольник и т. д.) относительно взаимно перпендикулярных центральных осей при повороте их на произвольный угол.

Расчётно-графическая работа №4.

Расчеты на прочность и жесткость при кручении.

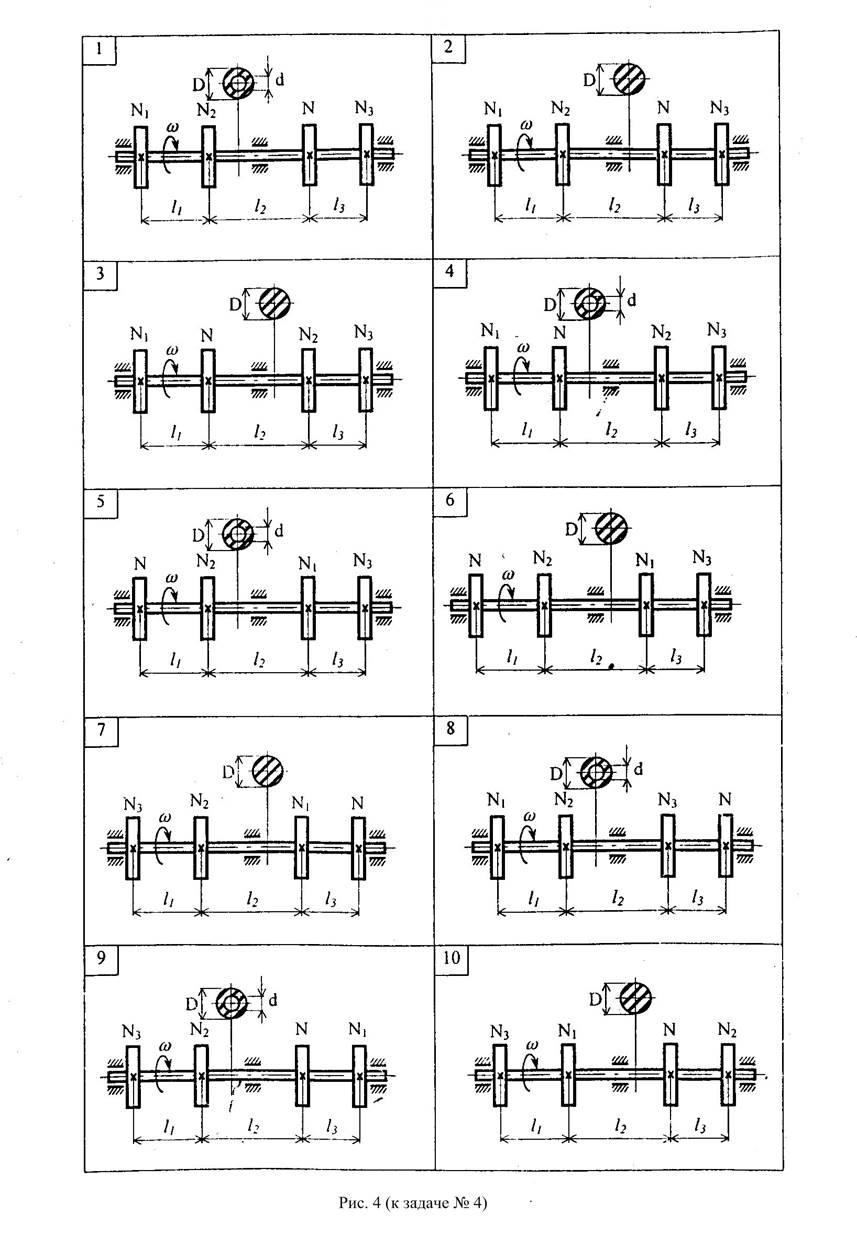
Для заданного трансмиссионного вала постоянного сечения со шкивами (рис.6), к которому при постоянной угловой скорости со подводится мощность N и снимаются мощности Ni требуется:

1. Построить эпюру крутящих моментов в сечениях вала.

2. Определить размеры поперечных сечений вала из условия прочности. При найденных размерах построить эпюру углов поворота сечений стержня, условно считая левый шкив неподвижным.

3. Определить размеры поперечных сечений вала из условия жесткости. При найденных размерах определить величину максимального напряжения в сечениях стержня.

Данные, необходимые для решения задачи, выбрать из таблицы вариантов (Табл.5). При решении задачи модуль сдвига принять: для стали G=80000 МПа. для чугуна — G=50000 МПа. Допускаемые касательные напряжения принять: для стали — [τ]=0,5[σ], для чугуна — [τ]=0,6[σ]р Механические свойства материалов приведены в Приложении 1. Принять допускаемый относительный угол закручивания[θ]0=1град/м (или 0,0175·10-3 рад/мм).Коэффициент запаса прочности принять для всех вариантов: стальных стержней n=1,5; чугунных стержней n=2.

4) При найденных размерах сечения вала определить потенциальную энергию упругой деформации.

Указания к выполнению работы

1.  Для определения незаданной мощности (внешнего момента) использовать условие равновесия вала.

2.  По известным мощностям и угловой скорости вала определить приложенные к шкивам внешние крутящие моменты. Используя метод сечений определить крутящие моменты в сечениях вала и построить их эпюру.

3.  Определить размеры сечения вала из условия прочности, а затем из условия жёсткости, сравнить полученные значения, выбрав максимальное значение диаметра вала для расчётов.

4.  Моменты сопротивления вращению вала, возникающие в опорах (подшипниках) не учитывать.

Таблица 5

Вопросы для защиты расчётно-графической работы №4

1.Что такое чистый сдвиг, закон парности касательных напряжений. Как

формулируется закон Гука при сдвиге?

2. Какой случай деформации стержня называют кручением. Что называется

крутящим моментом в поперечном сечении, как его вычисляют?

3. Какие гипотезы положены в основу вывода соотношений для определения

напряжений и деформаций?

4. Какие напряжения возникают и как они распределяются в сечениях при

кручении стержня круглого поперечного сечения. Как найти касательное

напряжение в произвольной точке такого стержня?

5. Сформулировать условие прочности стержня при кручении?

6. Что называется углом закручивания. Что называется жёсткостью стержня

при кручении. Как вычисляют полный угол закручивания ступенчатого

стержня?

7. Что такое полярный момент инерции сечения, момент сопротивления

кручению?

8. Сформулировать условие жесткости стержня при кручении?

9. Как объяснить различный характер разрушения стального и чугунного

стержня при кручении?

10.Как определяется потенциальная энергия при кручении вала?

11. Как раскрывают статическую неопределимость задачи при кручении?

12. Какие допущения принимаются при расчетах на срез, как формулируется

условие прочности и выбираются допускаемые напряжения?

13. Какие допущения принимаются при расчетах на смятие, как

формулируется условие прочности и выбираются допускаемые напряжения?

14. Как распределяются касательные напряжения по контуру прямоугольного

поперечного сечения стержня при кручении?

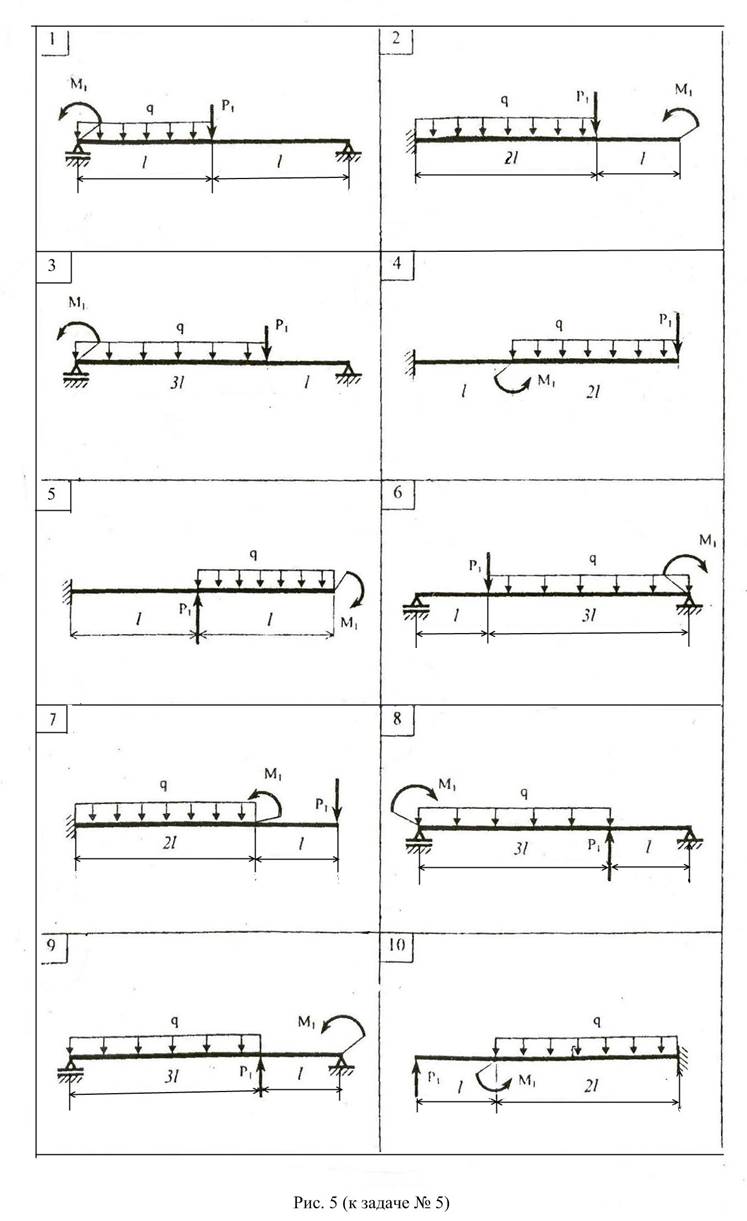
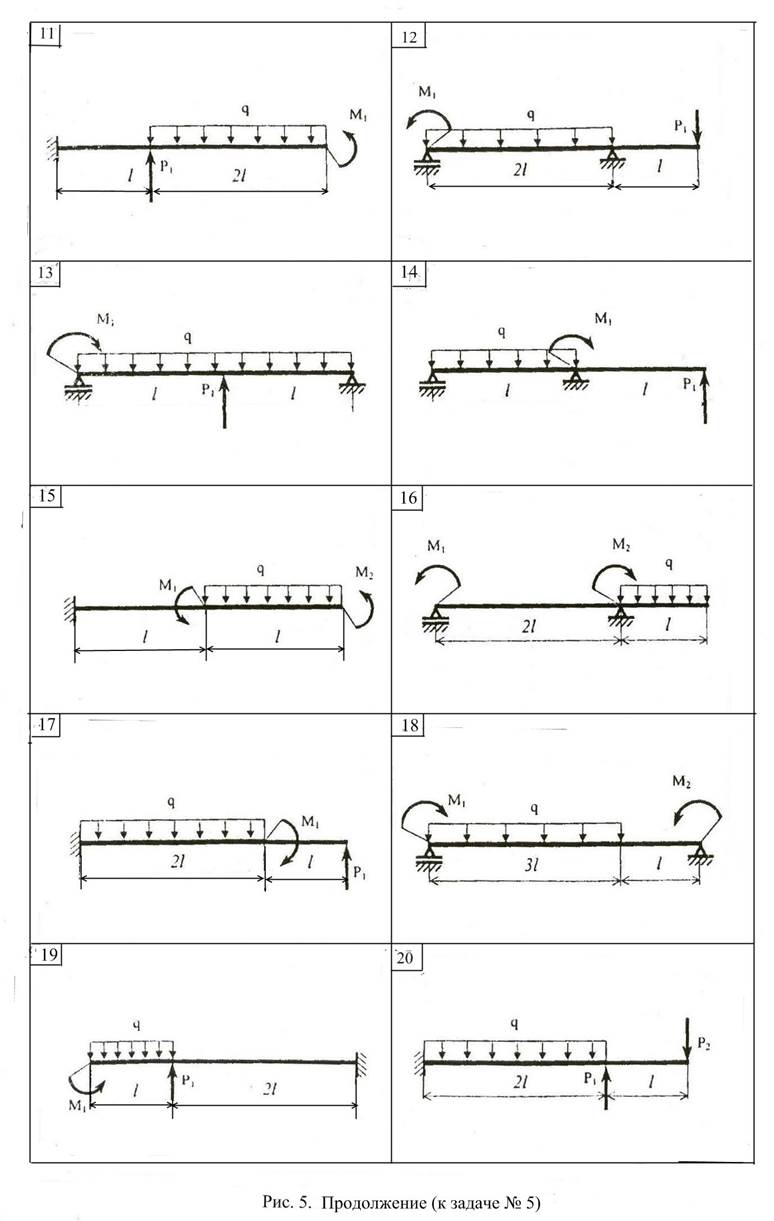
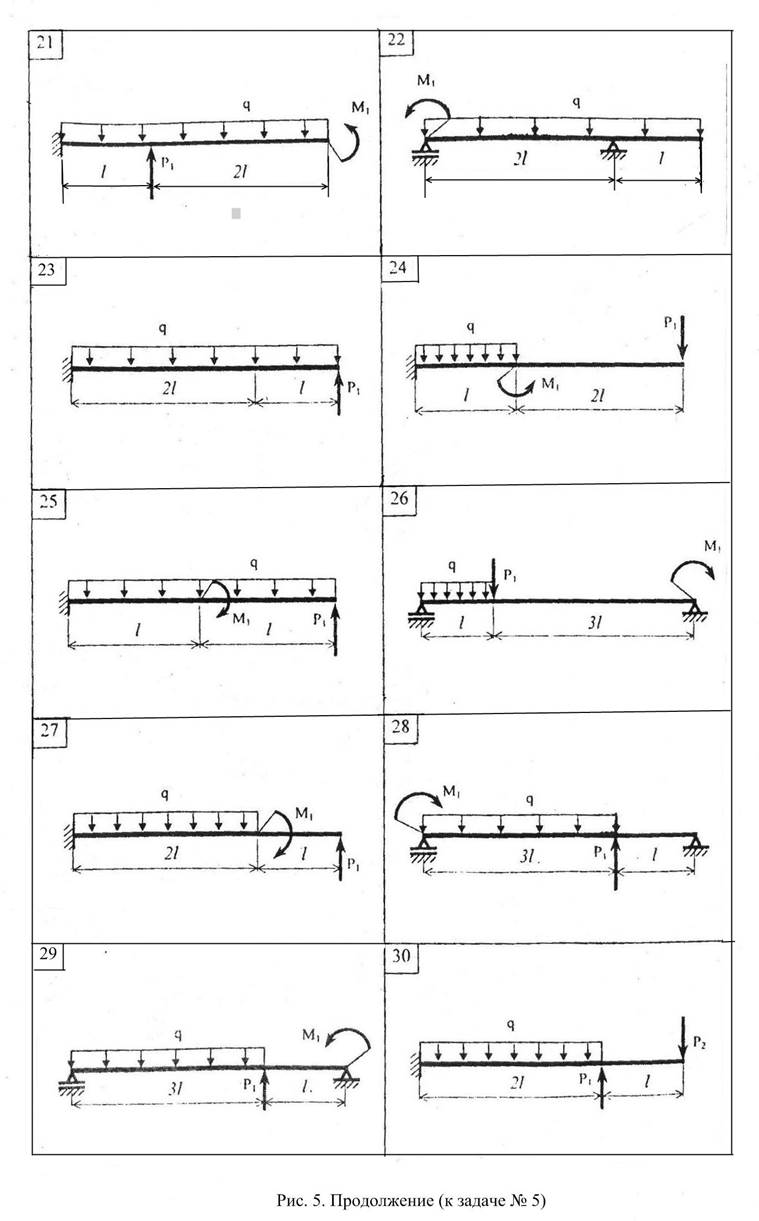
Задача №5: Расчёты на прочность при изгибе.

Для заданной стальной балки (рис.5) требуется:

1. Определить реакции опор, построить эпюры изгибающих моментов и перерезывающих сил в общем виде.

2. Определить величину допускаемой внешней нагрузки q из условия прочности, принимая поперечное сечение балки двутаврового профиля заданного номера.

3. Для рассчитанной величины внешней нагрузки, из условия прочности, подобрать прямоугольное поперечное сечение со сторонами h — большая, b — меньшая, отношение сторон h/b=2. Определить соотношение расхода материала на единицу длины балки для прямоугольного и двутаврового сечений.

4. Построить эпюры нормального и касательного напряжения в поперечных сечениях балки. Проверить прочность балки по касательным напряжениям.

5. Определить прогиб для одного сечения и угол поворота для другого сечения, интегрированием дифференциального уравнения упругой линии балки.

Данные, необходимые для решения задачи, выбрать из таблицы вариантов (Табл.6). При решении задачи модуль продольной упругости для стали принять — Е=200000 МПа. Механические свойства материалов стержней приведены в Приложении 1. Коэффициент запаса прочности принять для всех вариантов n=1,5. Допускаемые касательные напряжения для стали принять — [τ] = 0,5[σ]

6. Определить перемещение и угол поворота сечений балки из пункта
любым энергетическим методом. При определении перемещений
деформациями сдвига пренебречь, ввиду их малости.

Указания к выполнению работы.

1.  Для всех вариантов считать силовую линию совпадающей с вертикальной осью сечения балки

2.  Все расчёты при построении эпюр М и Q, определении перемещений выполнить в общем виде и лишь в расчётные формулы подставить необходимые данные, определяя числовые значения искомых величин.

Таблица№6

Вопросы для защиты расчётно-графической работы №5

Тема: Дифференциальное уравнение упругой балки.

1. Какими компонентами перемещений характеризуется изгиб балки?

2. С какой целью определяют перемещения балки?

З. Как проводится проверка жёсткости балки?

4. На чём базируется вывод дифференциального уравнения оси изогнутого

бруса?

5. Какое принято допущение при переходе от точного дифференциального

уравнения к приближённому, в каких случаях такое допущение будет

корректным?

6. В каком соответствии находятся знаки изгибающего момента и кривизны

для соответствующих положений координатных осей.

7. Каков геометрический смысл постоянных интегрирования

дифференциального уравнения упругой линии балки.

8. Какие приемы используют при интегрировании дифференциального

уравнения балки с несколькими участками. Как выравниваются константы

интегрирования на соседних участках?

9. Что представляют собой начальные условия задачи, с какой целью их

формулируют?

Тема: Энергетические методы определения перемещений.

1. Как вычисляется потенциальная энергия упругой деформации бруса в

общем случае нагружения бруса?

2. Сформулируйте понятие обобщённой силы и обобщённого перемещения.

3. Какие обобщённые перемещения обусловлены обобщёнными силами при

конкретной деформации бруса?

4. Сформулируйте теорему Кастилиано. В чем заключается неудобство при

определении перемещений по теореме Кастилиано.

5. В чём заключается приём, связанный с рассмотрением фиктивной силы при использовании теоремы Кастилиано?

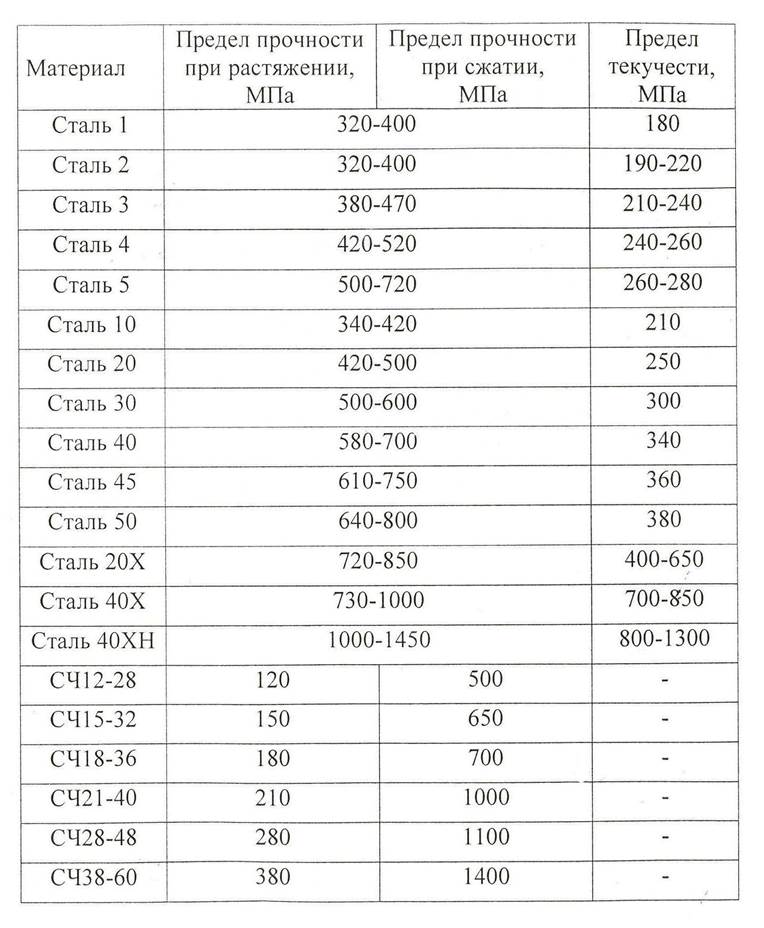
Приложение 1

Некоторые механические свойства конструкционных материалов.

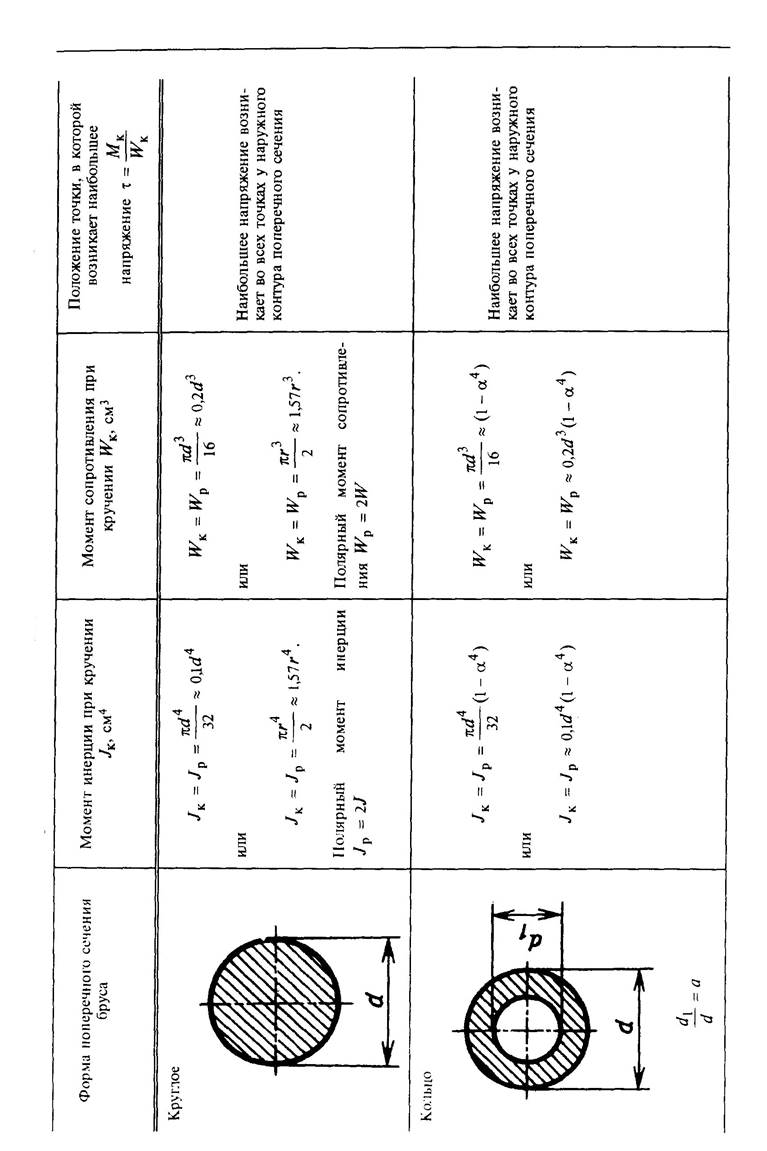
Приложение 2

Геометрические характеристики круглых поперечных сечений

Приложение 3

Значения тангенсов углов от 0° до 90°

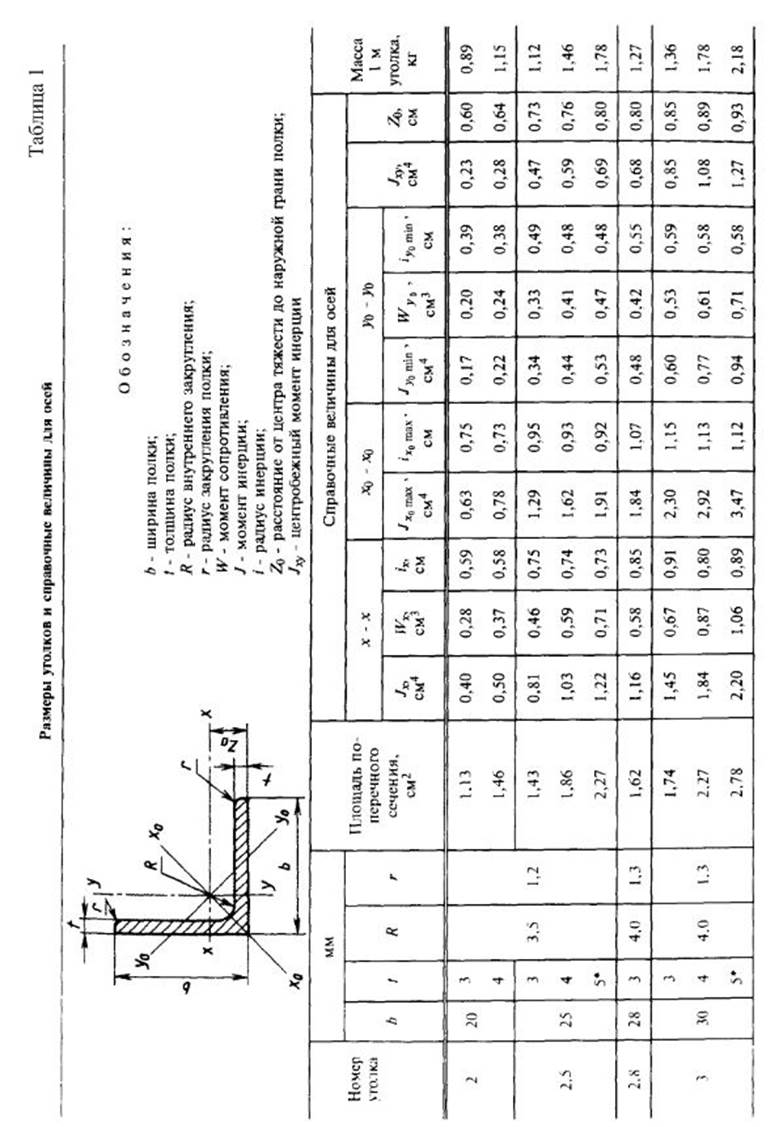
Приложение 4.

Справочные данные для стандартных профилей проката.

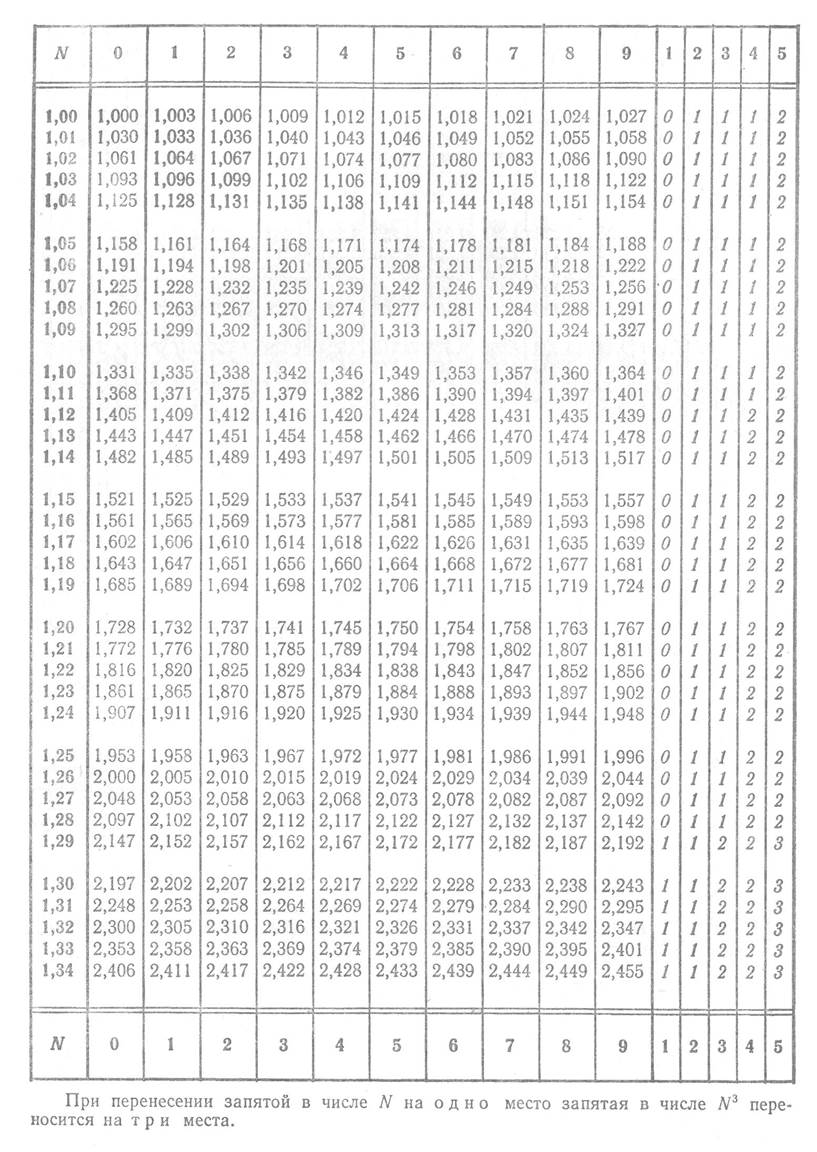
Приложение 5

Куб числа

Приложение 5 (продолжение)

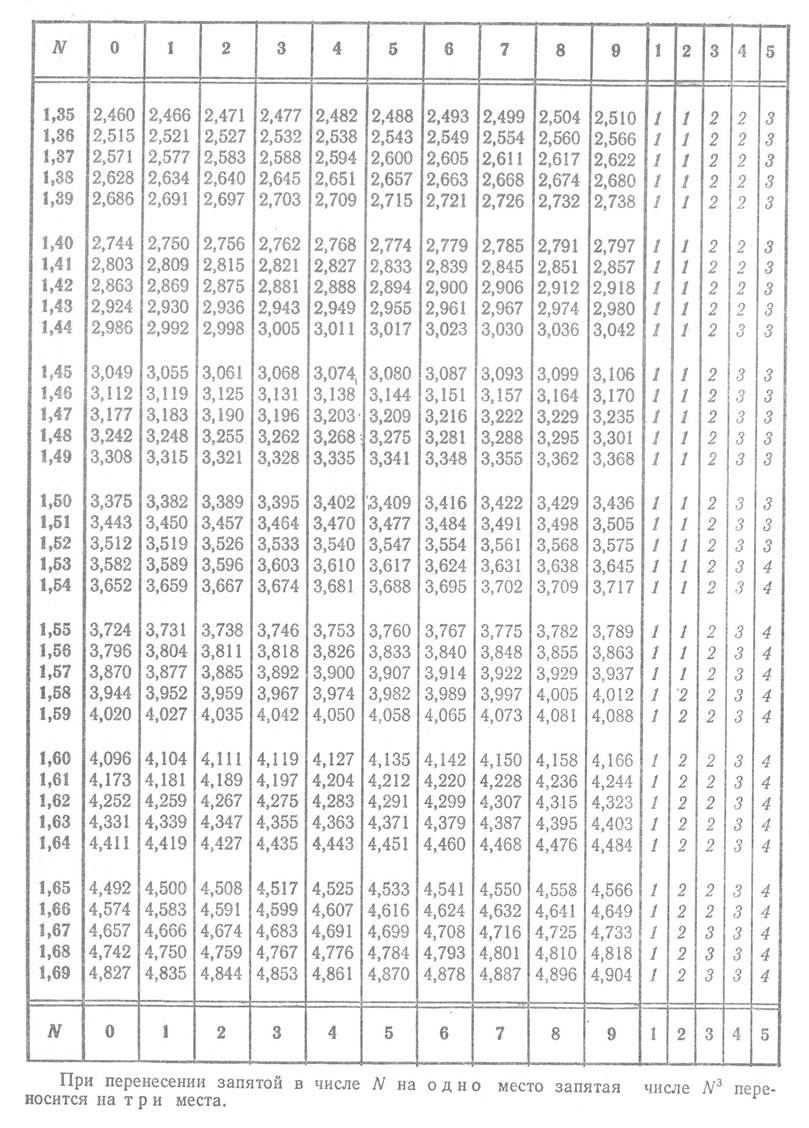
Приложение 5 (продолжение)

Приложение 5 (продолжение)

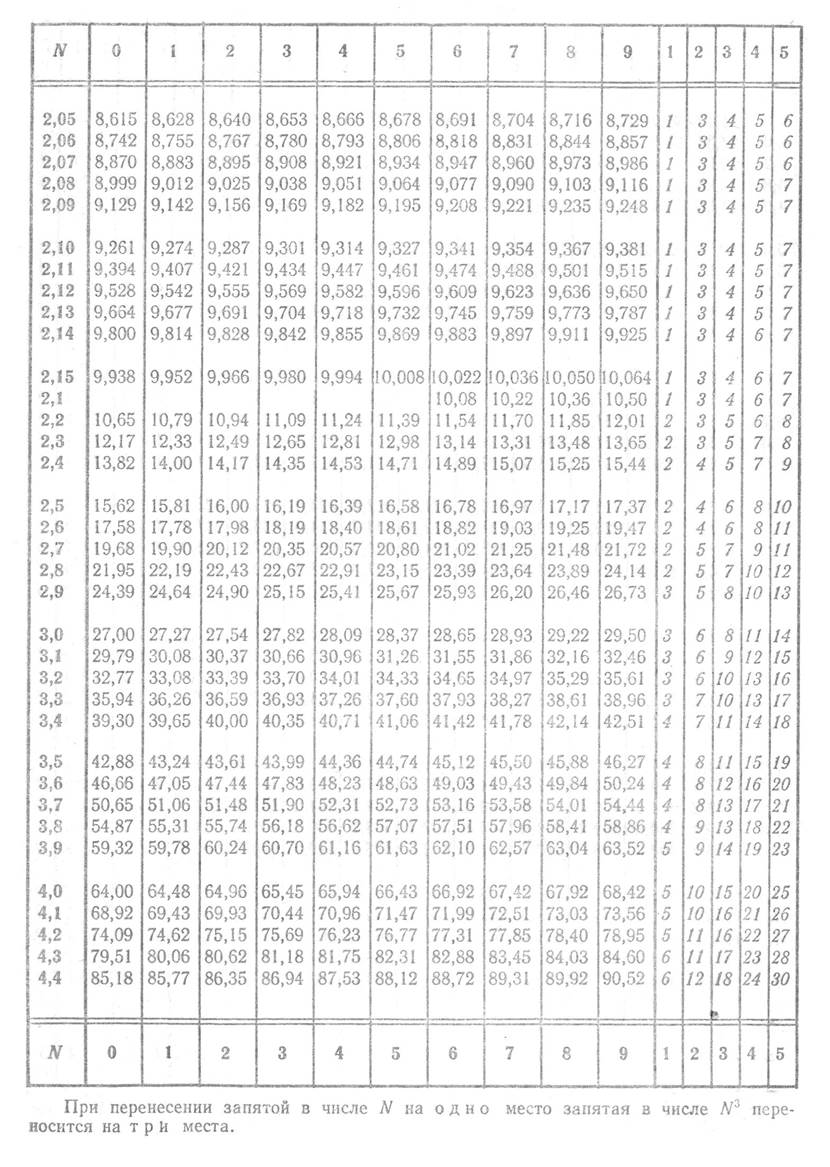
Приложение 5 (продолжение)

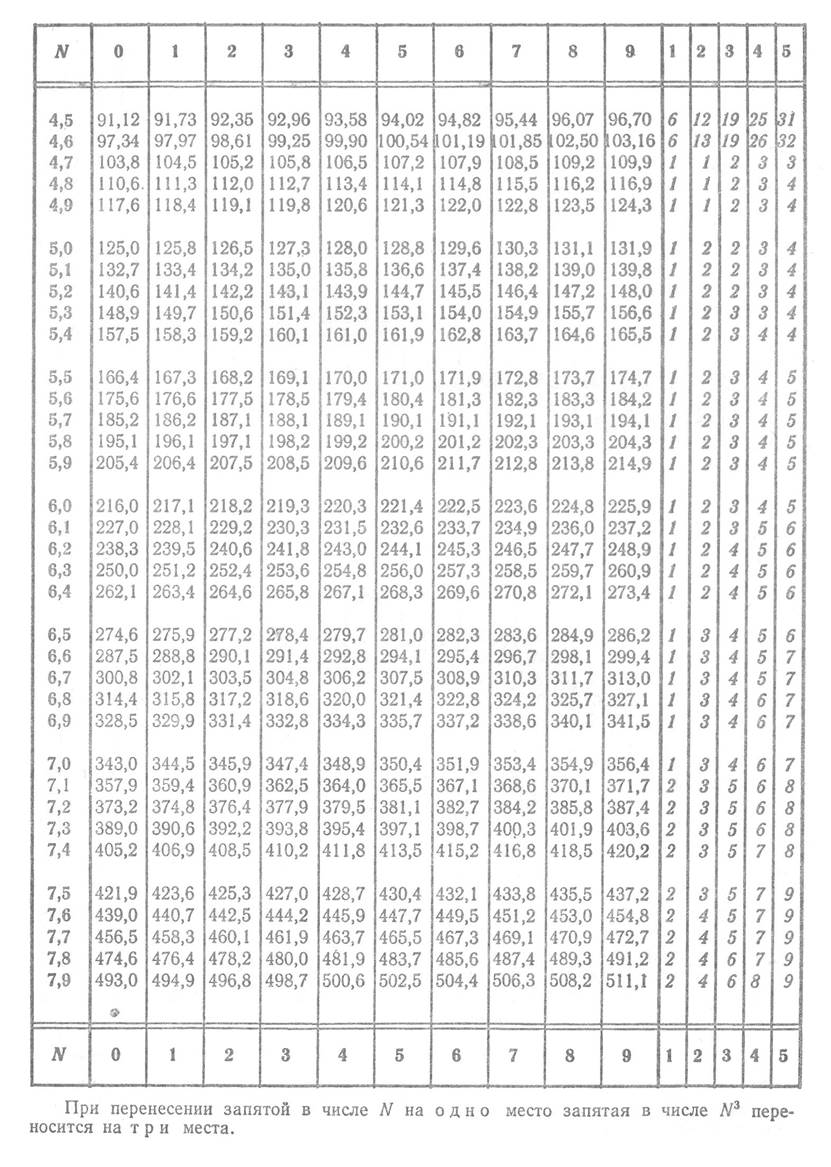
Приложение 5 (продолжение)

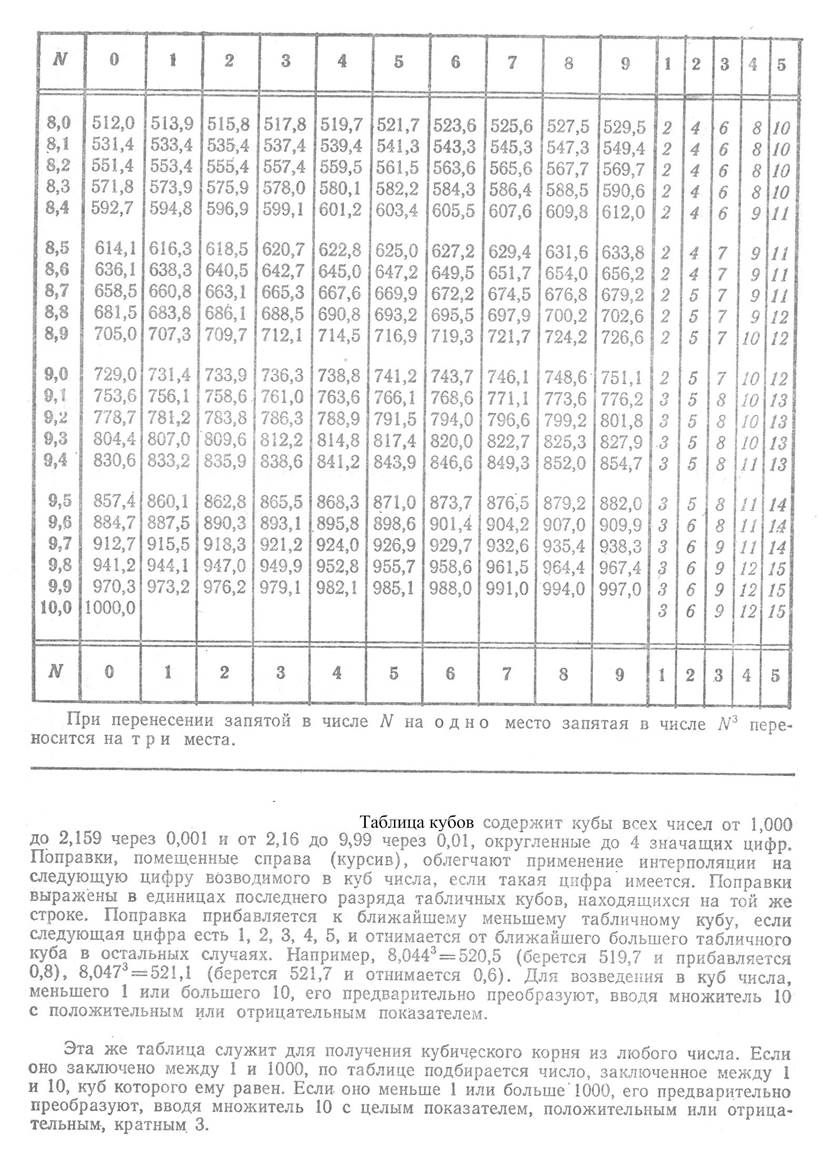
Приложение 6

Основные формулы и зависимости «Сопротивления материалов»