Статистическое толкование волн де-бройля

III. Статистическое толкование волн де-Бройля. Соотношение неопределенностей.

1.  Интерпретация волн де-Бройля.

Как уже отмечалось, заманчивая идея интерпретации частиц как волновых образований, проистекавшая, прежде всего, из равенства , не смогла выстоять, натолкнувшись, по крайней мере, на два противоречия. Во-первых, волновой пакет расплывается за время порядка с, во-вторых, такая «частица» должна разрушаться, попадая на дифракционную решетку.

Трудности «чисто» волновой теории становятся ещё более очевидными, если внимательно исследовать сами эксперименты по дифракции волн вещества.

Одной из гипотез, выдвинутых для объяснения существования волн материи, было предположение о том, что волны де-Бройля являются следствием коллективных эффектов, т. е. совместных действий многих частиц.

Однако при наблюдении дифракции электронов экспериментально было установлено, что счетчики, расположенные в области дифракционных максимумов, показывают скорость счета, пропорциональную интенсивности первичного пучка электронов даже при стремлении последней к нулю. Т. о., точка зрения, что волны материи образуются в среде с большим числом частиц, оказалась неверной. Даже единичные электроны (т. е. в случае, когда взаимодействие между электронами не играет никакой роли) дают интерференционную картину. Следовательно, отдельные частицы проявляют волновые свойства.

Рассмотрим интерференционный опыт с пучками малой интенсивности («единичными» электронами).

Направим на преграду с двумя узкими щелями параллельный

пучок моноэнергетических электронов, прохождение которых

через препятствие будем регистрировать с помощью

фотопластинки (Фп).

Если открывать поочередно одну или другую щель и проводить

экспонирование в течение некоторого конечного промежутка

времени, то «почернение» на фотопластинке будет

характеризоваться кривыми 1 и 2, соответственно.

Если открыть обе щели одновременно, то получающаяся

картина (3) не будет эквивалентна наложению двух первых

(1 и 2). Она оказывается аналогичной картине, получающейся

при интерференции двух когерентных световых волн.

Характер картины свидетельствует о том, что на движение каждого электрона оказывают влияние оба отверстия. Такой вывод несовместим с представлением о траекториях, приписываемых частицам. Если бы электрон в каждый момент времени находился в строго определенной точке пространства, то он проходил бы через определенное отверстие – первое или второе. Явление дифракции доказывает, что в прохождении каждого электрона через преграду участвуют оба отверстия. Нельзя, однако, представить дело таким образом, что какая-то часть электрона проходит через одно отверстие, а другая часть – через второе.

Сочетая в себе свойства волны и частицы, микрочастица обнаруживают существенное отличие от волны. Никто никогда не наблюдал полэлектрона, в то время как волну можно разделить на части, например, направив на полупрозрачное зеркало, и воспринимать затем каждую в отдельности. Микрочастица в отличие от волны всегда обнаруживается как неделимое целое с присущим ей массой, зарядом и другими характерными для неё параметрами.

Подтверждение своеобразия микрочастиц можно получить, наблюдая в эксперименте по дифракции электронов интерференционные кольца Дебая-Шерера.

Опыт показывает, что интерференционная картина не является непрерывной, а образована большим числом отдельных дискретных точек. При уменьшении интенсивности падающей волны пропорционально уменьшается число этих точек. В пределе очень низкой интенсивности можно наблюдать до одной точки, расположенной либо на месте центрального пятна, либо на дифракционных полосах или кольцах. Естественно приписать каждую точку воздействию прошедшей через систему частицы вещества.

Можно продолжить аналогию со светом и сделать вывод, что наиболее естественное истолкование дуализма волна – частица имеет статистическую основу в том смысле, что интенсивность волны в каждой точке экрана дает вероятность попадания частицы в эту точку.

Общепринятая в настоящее время интерпретация волн де-Бройля была предложена М. Борном. С позиций этого толкования весь ход событий в физической системе определяется вероятностными законами. Тому или иному положению частицы в пространстве соответствует некоторая вероятность, определяемая связанной с состоянием частицы волной де-Бройля.

Т. о., волны де-Бройля следует рассматривать как волны вероятности.

Интенсивность волн де-Бройля в данный момент времени и в данном месте определяет вероятность обнаружить частицу в данное время и в данном месте.

Исходя из аналогии c оптикой, можно ожидать, что определенного вида квадратичная форма, образованная из амплитуды волны, может быть истолкована как плотность потока или, иначе говоря, число рассеянных электронов. Расчеты, проделанные для различных процессов рассеяния, дают все основания верить в правильность принципа, связывающего амплитуду волны с числом частиц, иначе говоря, с вероятностью.

Интенсивность волны пропорциональна квадрату её амплитуды. Вероятность обнаружения частицы в элементе объема связывают с квадратом модуля амплитуды волны де-Бройля. Это обусловлено тем, что сама волновая функция может быть комплексной, в то время как величины, допускающие физическую интерпретацию, должны быть заведомо вещественными.

Итак, в опыте при прохождении щелей однозначно предсказать, куда попадет электрон, невозможно, можно лишь определить вероятность этого попадания.

Пусть 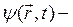определяет амплитуду волн де-Бройля, иначе, волновая функция, описывающая поведение частицы.

Вероятность обнаружить частицу в каком-либо месте пространства пропорциональна квадрату модуля амплитуды волны де-Бройля:

= .

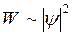Поведение свободной частицы может быть описано с помощью уравнения плоской волны:

,

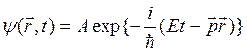для свободной частицы 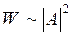, т. е. свободная частица равновероятно может быть обнаружена в любой точке пространства.

Если частица находится в силовом поле, то она уже не может быть представлена плоской волной и 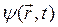имеет, вообще говоря, непериодический характер, но, по-прежнему, определяет вероятность обнаружения частицы в пространстве. Согласно Борну

,

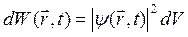где — элемент объема. Отсюда вытекает, что квадрат модуля волновой функции имеет смысл плотности вероятности нахождения (обнаружения) частицы в соответствующей области пространства.

Волновая функция 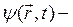ненаблюдаемая величина. Физический смысл этой величины связывается с квадратом её модуля .

Если частица существует, то её обнаружение в какой-либо точке пространства есть достоверное событие, поэтому должно выполняться условие нормировки:

.

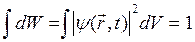Иногда нормировка невозможна, например, в случае свободной частицы.

2. Соотношение неопределенностей.

Итак, мы установили, что движущаяся частица, импульс которой равен , обнаруживает свойства, присущие волне, причем соотношение между длиной волны и импульсом частицы

,

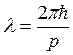введенное де-Бройлем, является универсальным, т. е. справедливым для любых частиц.

В то же время свойство реальной физической частицы нельзя свести к свойствам более привычных нам объектов, например, сконструировать её в виде волнового пакета. Волновые и корпускулярные свойства физических частиц являются различными аспектами их внутренней природы.

Рассмотрим состояние движения частицы, интересуясь положением и импульсом частицы в момент времени . Такое состояние описывается волновой функцией .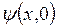

Как было сказано выше, в общепринятой в настоящее время интерпретации М. Борна амплитуда волны де-Бройля должна быть истолкована в понятиях вероятности.

Частицу вероятнее всего обнаружить там, где амплитуда её волновой функции велика. Если начальная волновая функция такова, что её амплитуда равна нулю всюду за пределами малой области, то можно утверждать, что в момент времени частица находится в пределах этой малой области и её положение известно довольно точно. Напротив, если начальная волновая функция распространяется на большую область, в пределах которой её амплитуда меняется мало, то частице нельзя приписать определенное положение, т. е. в момент времени положение частицы известно с большой неопределенностью. Мерой вероятности обнаружения частицы является квадрат абсолютного значения волновой функции.

Т. о., из волновых представлений следует, что точное положение частицы в данный момент времени, вообще говоря, не может быть задано, а точность, с которой это положение известно, зависит от состояния движения (волновой функции) частицы.

Аналогичные соображения справедливы и для другой переменной – импульса. Поскольку импульс и длина волны частицы связаны соотношением де-Бройля, понятно, что нельзя точно знать импульс, если плохо определена длина волны. В свою очередь, чтобы указать длину волны необходимо, чтобы волновая функция имела хотя бы некоторые свойства периодичности. Поэтому точность определения импульса также зависит от состояния движения частицы – для протяженной синусоидальной волны он может быть определен весьма точно и, наоборот, в случае волны произвольной формы, для которой понятие длины волны вообще неприменимо, лишь очень грубо.

Гейзенберг показал, что, хотя не существует пределов точности, с которой можно определить либо импульс, либо положение частицы, имеется принципиальный предел для точности определения этих величин в один и тот же момент времени, т. е. для данной волновой функции.

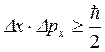(1)

Рассмотрим, как можно прийти к соотношению неопределенностей, описывая движение частицы волновой функцией .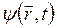

Пусть имеется свободная частица. Её волновая функция может быть представлена уравнением плоской волны:

,

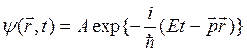и плотность вероятности

.

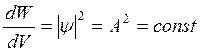Такой частице сопоставляется монохроматическая волна де-Бройля с определенным значением , поэтому из соотношения де-Бройля может быть найден импульс частицы. Однако такая (свободная) частица делокализована, т. е. с одинаковой вероятностью может быть обнаружена в любой точке пространства. Т. о., пытаться определить траекторию движения частицы бессмысленно.

Чтобы локализовать частицу в некоторой области пространства (в одномерном случае – в интервале

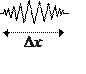значений ), следует сопоставить ей некий пакет волн,

который может быть представлен интегралом Фурье:

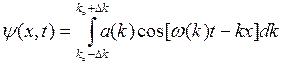. (2)

Для волнового пакета возможные значения длины волны заключены в некотором интервале, т. е. существует некоторая неопределенность в определении её значения. В отличие от свободной частицы, для которой в любой точке пространства амплитуда волновой функции отлична от нуля, амплитуда волнового пакета, соответствующего пространственно локализованной частице, отлична от нуля на отрезке ~ .

Т. о., пространственной локализации частицы соответствует формирование волнового пакета путем суперпозиции волн де-Бройля.

Протяженность волнового пакета можно определить как промежуток, в пределах которого импульс существенно отличается от нуля. Соответственно, интервал значений модуля волнового вектора , на котором амплитуда волнового спектра существенно отлична от нуля, определяет ширину спектра волнового пакета. Причем, чем меньше протяженность волнового пакета, тем больший набор гармоник необходим для его формирования.

Рассмотрим волновой пакет (2) в момент времени , положив

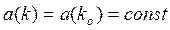
во всем интервале изменения значений волнового числа .

Тогда

,

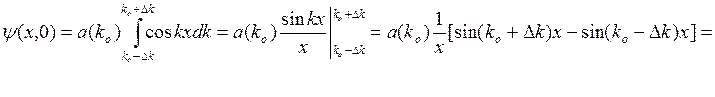
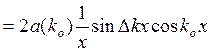где 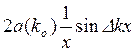— медленно меняющаяся амплитуда.

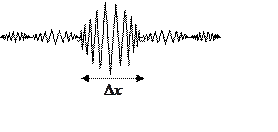Ближайшие нули:

;

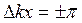
(последующие максимумы амплитуд незначительны по

сравнению с основным максимумом), откуда

протяженность волнового пакета может быть найдена как

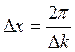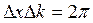и . (3)

Умножая (3) на , получаем

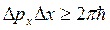, (4)

где и 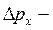разброс значений, или неопределенность координаты и импульса частицы в направлении оси .

Т. о., произведение этих величин не может быть меньше . В то же время при рассмотрении различных конкретных примеров в правой части соотношения (4), вообще говоря, могут быть получены разные значения, пропорциональные : 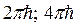и т. д.

Однако, если под неопределенностью измеряемых величин понимать среднеквадратичные отклонения физических величин от их среднего значения, т. е.

,

,

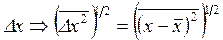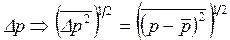то соотношение (4) приводится к виду:

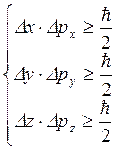, (5)

Выражения (5) называются соотношениями неопределенностей Гейзенберга, которые определяют абсолютный предел точности одновременного измерения (для данной волновой функции) величин, связанных соотношением (5), который в самой благоприятной ситуации достижим, но не может быть превзойден ни при каких обстоятельствах.

Величины 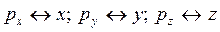называют канонически сопряженными. Кроме рассмотренных пар, существуют и другие канонически сопряженные величины, например, , .

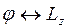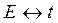Оказывается, что соотношение неопределенностей всегда выполняется для любой пары канонически сопряженных (иначе, дополнительных друг другу) величин:

если 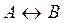, то .

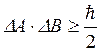Произведение неопределенностей значений двух сопряженных переменных не может быть меньше .

В то же время произведение неопределенностей определения, например, переменных и не подчиняется этому правилу:

,

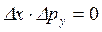т. е. можно одновременно без ограничения точности измерить координату и — компоненту импульса частицы.

Обратимся теперь к соотношению неопределенностей, связывающему энергию и время, которое имеет достаточно сложное содержание.

1.  Пусть частица находится в стационарном состоянии. Тогда из соотношения неопределенности следут, что определение её энергии с точностью должно занять время, по меньшей мере, .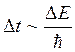

Т. е. мы связаны с процессом наблюдения (измерения), и чем меньше время наблюдения, тем меньше и определенность энергии.

2. Частица (система) находится в возбужденном (нестационарном) состоянии.

В этом случае интерпретируется как разброс энергий (ширина энергетического уровня) в этом

состоянии, а 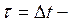время жизни возбужденного состояния.

Иногда соотношение неопределенностей получает следующее толкование: в действительности у микрочастицы имеются точные значения координат и импульсов, однако ощутимое для такой частицы воздействие измерительного прибора не позволяет точно определить эти значения.

Такое толкование является совершенно неправильным. В частности, оно противоречит наблюдаемым в опытах явлениям дифракции микрочастиц.

Соотношение неопределенностей обусловлено корпускулярно-волновой природой микрообъектов. Оно указывает, в какой мере можно пользоваться понятиями классической механики применительно к микрочастицам, в частности, говорить о траекториях микрочастиц.

Понятие траектории связывается с возможностью указать в каждый момент времени вполне определенные значения координат и скорости частицы. Заменив в выражении (1) на , получим соотношение

.

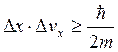Очевидно, что чем больше масса частицы, тем меньше неопределенности её координаты и скорости и, следовательно, тем больше оснований для характеристики движения частицы использовать траекторию.

При определенных условиях даже движение микрочастицы можно описывать траекторией. Примером может служить движение электрона в электронно-лучевой трубке.

Пусть длина трубки 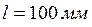, а след электронного пучка на экране имеет радиус 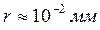. Это дает погрешность в определении импульса электрона 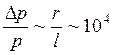. Импульс электрона мы найдем, положив ускоряющее напряжение в трубке равным 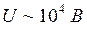. Тогда из 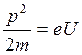получаем

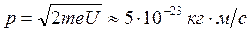и ,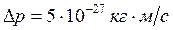

и, наконец,

.

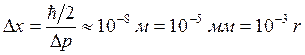Понятно, что для описания движения электрона в электронно-лучевой трубке применимо понятие траектории.

Квантовая механика.

Квантовая механика – теория, устанавливающая способ описания и законы движения микрочастиц (элементарных частиц, атомных ядер, атомов, молекул) и их систем (например, кристаллов), а также связь величин, характеризующих частицы и образованные ими системы, с физическими величинами, непосредственно измеряемыми на опыте.

Теория атома Бора, с точки зрения Гейзенберга (1925 г.), несостоятельна потому, что опирается на фундаментальные идеи (прежде всего это картина орбит электронов и справедливость классических законов движения), которые никогда и никоим образом не могут быть проверены, поскольку они ускользают от наблюдения.

Так теория Бора говорит об орбите электрона и о скорости его движения, не принимая во внимание то, что мы вообще не можем определить положение электрона в атоме, не разрушив при этом весь атом.

Действительно, чтобы погрешность в определении положения электрона в атоме была значительно меньше размера самого атома (размер последнего порядка нескольких ангстрем), мы должны наблюдать атом в свете с существенно меньшей длиной волны, т. е. облучать его жесткими рентгеновскими или лучами.

Однако в этом случае комптоновская отдача электрона будет столь велика, что его связь с атомом немедленно разорвется.

Т. о., следуя боровской теории, мы выходим за пределы опыта. Поэтому не следует удивляться, что теория, построенная на основе гипотез, не допускающих экспериментальной проверки, оказывается частично несостоятельной в тех выводах, которые могут быть проверены на опыте.

При построении логически непротиворечивой схемы атомной механики в теорию нельзя вводить никаких величин, кроме физически наблюдаемых. Нельзя, скажем, ввести орбиту электрона, но следует отталкиваться лишь от наблюдаемых частот и интенсивностей линий излучения атома.

Исходя из этого принципа, Гейзенберг заложил основы теории, развитой им самим, Борном и Йорданом (1925 г.), призванной заменить атомную механику Бора и весьма успешной во всех её применениях.

Эта теория получила название матричной механики.

Матричная механика.

Хотя по своей форме матричная механика совершенно отлична от волновой механики, о которой мы будем говорить ниже, как показал Шрёдингер, обе теории идентичны.

В силу этого и поскольку основным предметом изучения будет являться волновая механика, мы лишь кратко остановимся на основном содержании матричной механики.

Поскольку отправной точкой наших рассуждений служат частоты

,

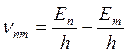как наблюдаемые величины, то, следуя Борну, разместим их в виде квадратной таблицы:

.

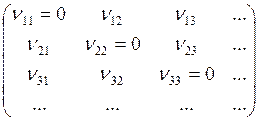Если теперь придерживаться такой схемы размещения, так что, скажем, место в четвертой строке и втором столбце всегда будет ассоциировано с переходом из четвертого во второе квантовое состояние, то можно расставить в подобной квадратной таблице и амплитуды “осцилляторов”, связанных с различными излучаемыми частотами, причем будет обозначать тогда интенсивность излучения соответствующей частоты: