Температурные напряжения в длинном толстостенном упругом цилиндре
 – функция Хевисайда.
– функция Хевисайда.
17. Температурные напряжения в длинном толстостенном упругом цилиндре.
Цилиндр, внутренний радиус которого a=10 см, наружный b=25 см, находится в состоянии стационарного неравномерного нагрева, причем температура на внутренней поверхности цилиндра на 200 градусов больше, чем на наружной поверхности. Построить для напряжений  графики зависимостей от радиуса
графики зависимостей от радиуса ![]() . Предположить, что труба не несет осевой нагрузки. Параметры материала цилиндра выбрать самостоятельно.
. Предположить, что труба не несет осевой нагрузки. Параметры материала цилиндра выбрать самостоятельно.
18. Температурные напряжения в толстостенной упругой сфере
Найти температурные напряжения в полой сфере, нагретой симметрично относительно центра, считая тепловое состояние сферы стационарным. Дано : а= 10 см, b=12 см, 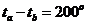 . Построить графики зависимостей напряжений
. Построить графики зависимостей напряжений ![]() от радиуса
от радиуса ![]() . Параметры материала сферы выбрать самостоятельно.
. Параметры материала сферы выбрать самостоятельно.
19. Напряженное и деформированное состояние призматического стержня под действием собственного веса
Найти напряженное и деформированное состояние (распределение перемещений) в упругом призматическом стержне прямоугольного сечения, «стоящем» на горизонтальном неподвижном основании при действии поля сил тяжести. Для нижнего сечения стержня принять следующие граничные условия: касательные напряжения отсутствуют, нормальные напряжения распределены равномерно. Придумать физическую интерпретацию закрепления, реализующего данные граничные условия. Изобразить зависимости распределения перемещений точке упругого параллелепипеда.
20. Напряженное и деформированное состояние призматического стержня под действием собственного веса
Упругий призматический стержень прямоугольного сечения (прямоугольный параллелепипед) вставлен без зазоров в абсолютно жесткую (недеформируемую) матрицу. Боковые стенки и днище матрицы – плоскости. Верхний торец стержня свободен от нагружения. Все находится в поле силы тяжести. Найти напряженное и деформированное (перемещения) состояние упругого параллелепипеда. Предположить, что нормальные напряжения на нижнем торце параллелепипеда распределены равномерно по площади, касательные напряжения на поверхностях контакта не возникают. Изобразить зависимости распределения перемещений точек упругого параллелепипеда.
21. Температурные напряжения в длинном толстостенном упругом цилиндре
Цилиндр, внутренний радиус которого a=10 см, наружний b=25 см, находится в состоянии стационарного неравномерного нагрева, причем температура на внутренней поверхности цилиндра на 150 градусов больше, чем на наружной поверхности и распределена по толщине стенки цилиндра по закону  .Предположить, что в продольном направлении деформирование цилиндра ничем не стеснено (суммарное усилие в продольном направлении в стержне положить равным нулю). Построить для напряжений
.Предположить, что в продольном направлении деформирование цилиндра ничем не стеснено (суммарное усилие в продольном направлении в стержне положить равным нулю). Построить для напряжений  графики зависимостей от радиуса r. Параметры материала цилиндра выбрать самостоятельно.
графики зависимостей от радиуса r. Параметры материала цилиндра выбрать самостоятельно.
22. Температурные напряжения в длинном упругом цилиндре
Допустим, что электрический ток вызывает повышение температуры внутри длинного цилиндрического, прямого сплошного проводника радиуса b, постоянное по длине. Можно показать, что относительное повышение температуры в проводнике на некотором расстоянии r от центра определяется формулой  , где
, где 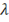 постоянная. Предположим, что напряжения не превышают предела упругости и что отсутствуют внешние силы, препятствующие продольному и поперечному расширению. Найти напряжения, вызываемые данным температурным полем. Построить графики распределения напряжений. Параметры цилиндра (проводника) выбрать самостоятельно.
постоянная. Предположим, что напряжения не превышают предела упругости и что отсутствуют внешние силы, препятствующие продольному и поперечному расширению. Найти напряжения, вызываемые данным температурным полем. Построить графики распределения напряжений. Параметры цилиндра (проводника) выбрать самостоятельно.
23. Напряженное и деформированное состояние упруго-вязкой сферы
Толстостенная сфера, на внутренней поверхности нагружается внезапно возникшим давлением
 – функция Хевисайда, наружняя поверхность сферы свободна от нагружения. Материал сферы про объемном деформировании демонстрирует чистую упругость, а в отношении деформации формоизменения соответствует реологической модели Максвелла. Найти напряженное и деформированное состояние сферы. Построить графики распределения напряжений и перемещений в стенках сферы и их зависимости от времени. Динамическими эффектами при деформациях сферы пренебречь.
– функция Хевисайда, наружняя поверхность сферы свободна от нагружения. Материал сферы про объемном деформировании демонстрирует чистую упругость, а в отношении деформации формоизменения соответствует реологической модели Максвелла. Найти напряженное и деформированное состояние сферы. Построить графики распределения напряжений и перемещений в стенках сферы и их зависимости от времени. Динамическими эффектами при деформациях сферы пренебречь.
24. Кручение стержня узкого прямоугольного поперечного сечения
Задано поперечное сечение стержня в виде узкого прямоугольника, т. е. размер b значительно меньше размера a. Показать, что в таком случае (если не считаться с особенностями на коротких сторонах ввиду их малой протяженности в общем периметре сечения) приближенно функция напряжений может быть назначена в виде
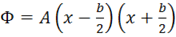 (ось 0x параллельна узкой стороне прямоугольника). Найти напряжения в сечении при указанной функции напряжения. Построить зависимость касательных напряжений по сечению стержня. Изобразить поверхность депланации сечения скручиваемого стержня.
(ось 0x параллельна узкой стороне прямоугольника). Найти напряжения в сечении при указанной функции напряжения. Построить зависимость касательных напряжений по сечению стержня. Изобразить поверхность депланации сечения скручиваемого стержня.
25. Кручение стержня непонятно какого поперечного сечения
Выяснить, может ли функция
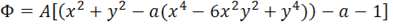 являться функцией напряжения при кручении стержня и каким контурам поперечного сечения она отвечает, если положить a=0, a=0.5
являться функцией напряжения при кручении стержня и каким контурам поперечного сечения она отвечает, если положить a=0, a=0.5 ,. Рассмотреть случай
,. Рассмотреть случай  . С помощью предложенной функции приближенно решить задачу о кручении стержня квадратного поперечного сечения.
. С помощью предложенной функции приближенно решить задачу о кручении стержня квадратного поперечного сечения.
26. Кручение стержня прямоугольного поперечного сечения
Решить задачу о кручении упргуого стержня прямоугольного (![]() сечения, принимая в качестве функции напряжений ее приближенной однопараметрическое выражение
сечения, принимая в качестве функции напряжений ее приближенной однопараметрическое выражение 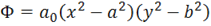 . Неизвестный коэффициент
. Неизвестный коэффициент ![]() определяется из условия минимума дополнительной работы скручиваемого стержня, приходящйся на единицу его длины
определяется из условия минимума дополнительной работы скручиваемого стержня, приходящйся на единицу его длины 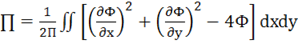
Сравнить жесткости на кручение стержня квадратного сечения и стержня круглого сечения, имеющих одинаковые площади поперечных сечений. Построить зависимости касательных напряжений от коодинат сечения стержня. Построить поверхность депланации сечения. Принять, например, ![]() .
.
26. Кручение стержня прямоугольного поперечного сечения
Решить задачу о кручении упргуого стержня прямоугольного (![]() сечения, принимая в качестве функции напряжений ее приближенной трехпараметрическое выражение
сечения, принимая в качестве функции напряжений ее приближенной трехпараметрическое выражение 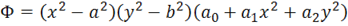 . Неизвестные коэффициенты
. Неизвестные коэффициенты  определяются из условия минимума дополнительной работы скручиваемого стержня, приходящйся на единицу его длины
определяются из условия минимума дополнительной работы скручиваемого стержня, приходящйся на единицу его длины 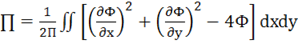
Сравнить жесткости на кручение стержня квадратного сечения и стержня круглого сечения, имеющих одинаковые площади поперечных сечений. Построить зависимости касательных напряжений от коодинат сечения стержня. Построить поверхность депланации сечения.


