Тензор квадрупольного момента
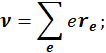
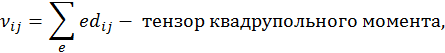
где
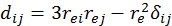 .
.
Тензор квадрупольного момента является симметричным:
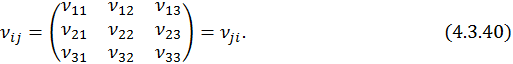
Очевидно, что
Следовательно, независимыми элементами тензора являются пять. Но ![]() можно привести к диагональному виду (к главным осям). В этом случае квадрупольный момент выглядит следующим образом:
можно привести к диагональному виду (к главным осям). В этом случае квадрупольный момент выглядит следующим образом:
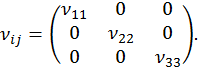
А так как ![]() равен нулю, то независимыми остаются только два элемента. Можно положить:
равен нулю, то независимыми остаются только два элемента. Можно положить:
![]()
если система обладает азимутальной симметрией, и остается всего один независимый элемент: 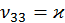 . Он и определяет квадрупольный момент, является внутренней характеристикой данной системы.
. Он и определяет квадрупольный момент, является внутренней характеристикой данной системы.
Можно показать, что для электрически нейтральной системы с равным нулю дипольным моментом системы, тензор квадрупольного момента не зависит от выбора начала координат. Положим, что 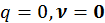 , тогда
, тогда
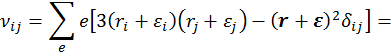
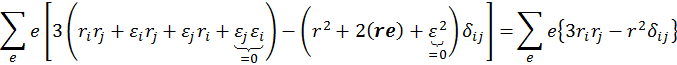
Здесь члены с ![]() и
и ![]() равны нулю, т. к.
равны нулю, т. к. 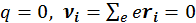 . Потенциал квадруполя согласно (4.3.39) имеет вид:
. Потенциал квадруполя согласно (4.3.39) имеет вид:
![]()
где 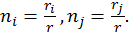
Здесь идет суммирование по i и j. Предположим, что система обладает азимутальной симметрией, тогда
![]()
С учетом этого получим:
![]()
Т. к. 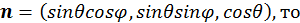
![]()
![]()
где 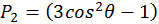 – полином Лежандра. В этом случае получаем следующий потенциал квадрупольного момента системы:
– полином Лежандра. В этом случае получаем следующий потенциал квадрупольного момента системы:
![]()
Обобщая данную формулу, получим потенциал n – того момента:
![]()
где
![]()
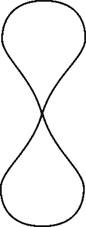
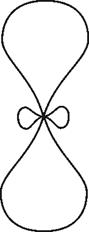
Для наглядности построим несколько эквипотенциальных поверхностей, задавая различные n:
|
n=0 |
кулоновский потенциал |
|
|
n=1 |
потенциал дипольного момента |
|
|
n=2 |
потенциал квадруполя |
|
|
n=3 |
потенциал октуполя |
|
§ 4.4. Системы зарядов в постоянном и неоднородном внешнем электрическом поле
Рассмотрим систему зарядов, находящихся во внешнем электрическом поле. Будем считать, что линии напряженности вектора электрического поля ![]() достаточно гладкие, т. е. поле меняется плавно от точки к точке. Внешнее электростатическое поле определяется уравнениями:
достаточно гладкие, т. е. поле меняется плавно от точки к точке. Внешнее электростатическое поле определяется уравнениями:
![]()
Энергия системы зарядов в этом случае определяется выражением:

где 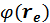 – потенциал внешнего поля в точке с радиус-вектором
– потенциал внешнего поля в точке с радиус-вектором ![]() . При этом пренебрегаем энергией взаимодействия самих зарядов. Т. к. внешнее поле плавно меняется в области где находятся заряды, то потенциал
. При этом пренебрегаем энергией взаимодействия самих зарядов. Т. к. внешнее поле плавно меняется в области где находятся заряды, то потенциал 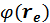 можно разложить в ряд Тейлора по малым
можно разложить в ряд Тейлора по малым ![]() .
.
![]()
где

Тогда потенциальная энергия системы запишется следующим образом:
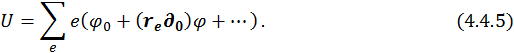
Рассмотрим два случая.
1. В нулевом приближении потенциальная энергия системы

Формально совпадает с потенциальной энергией точечного заряда (суммы всех зарядов системы), который находится в начале координат.
2. В первом приближении получаем потенциальную энергию электрического диполя, находящегося в начале координат:
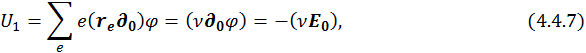
т. к. 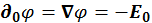 .
.
Если система в целом нейтральна, то этот член будет главным, а для нейтральной системы электрический дипольный момент не зависит от выбора начала координат.