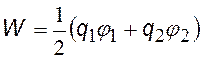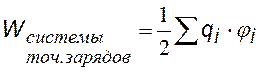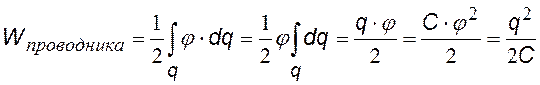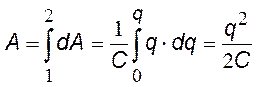Теорема гаусса при наличии диэлектрика
|
|
где n – концентрация молекул, a — поляризуемость молекулы, р0 — дипольный момент молекулы, k – постоянная Больцмана, T – абсолютная температура, e0 – электрическая постояннная |
|
|
Теорема Гаусса при наличии диэлектрика.
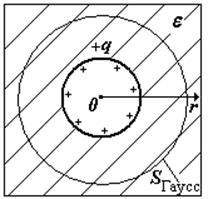
 Пусть заряд +q окружен оболочкой из твердого диэлектрика. На рисунке показаны схематически несколько молекул диэлектрика. Они стремятся ориентироваться по полю этого заряда. Диэлектрик поляризуется, на внешней его поверхности возникает связанный заряд +q¢связ , на внутренней —q¢связ. Допустим, мы хотим найти напряженность поля в диэлектрике с помощью теоремы Гаусса. Выбираем гауссову поверхность в виде сферы. Она будет охватывать не только заряд +q, но и отрицательные связанные заряды, как-бы «отсекая» часть молекулы.
Пусть заряд +q окружен оболочкой из твердого диэлектрика. На рисунке показаны схематически несколько молекул диэлектрика. Они стремятся ориентироваться по полю этого заряда. Диэлектрик поляризуется, на внешней его поверхности возникает связанный заряд +q¢связ , на внутренней —q¢связ. Допустим, мы хотим найти напряженность поля в диэлектрике с помощью теоремы Гаусса. Выбираем гауссову поверхность в виде сферы. Она будет охватывать не только заряд +q, но и отрицательные связанные заряды, как-бы «отсекая» часть молекулы.
|
|
теорема Гаусса для вектора напряженности при наличии диэлектрика. qсвоб = q, q¢связ — отрицательный связанный заряд, охватываемый гауссовой поверхностью. |
Найти связанный заряд q¢связ можно только в самых простых случаях. Но можно записать теорему Гаусса для вектора электрической индукции D.
|
|
|
Подставив эти формулы в (©), получим выражение для теоремы Гаусса в виде: |
|
|
Теорема Гаусса для вектора электрической индукции: «Поток вектора электрической индукции через произвольную замкнутую поверхность равен алгебраической сумме свободных зарядов, охватываемых этой поверхностью». |
|
Для определения напряженности поля при наличии диэлектрика следует использовать теорему Гаусса для электрической индукции D, а затем найти напряженность по формуле D=eeoE, тем самым мы избавляемся от необходимости нахождения связанных зарядов. |
|
|
Пример. Металлическая сфера, имеющая заряд q, помещена в жидкий диэлектрик (диэлектрическая проницаемость e). Найти напряженность поля в диэлектрике в зависимости от радиальной координаты r. Воспользуемся теоремой Гаусса.
|
|
|
При наличии диэлектрика с диэлектрической проницаемостью e во всех формулах надо заменить [16] |
e0 ® ee0 |
Электрическая энергия.
Заряженные тела обладают запасом энергии. Это проявляется, например, при отталкивании одноименно заряженных тел, когда они приобретают кинетическую энергию. При сближении разноименно заряженных тел между ними проскакивает искра, и мы наблюдаем переход запасенной электрической энергии в другие виды энергии: световую, звуковую, тепловую. Найдем выражения для энергии заряженных тел.
1)Два неподвижных точечных заряда.
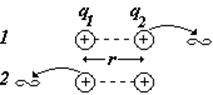
Пусть два точечных заряда q1 и q2 находятся на расстоянии r друг от друга. Найдем работу по переносу в бесконечность сначала одного заряда, затем другого
|
|
работа в 1-м и 2-м случаях;j2 — потенциал поля заряда q1 в точке, где находится q2; ;j1 потенциал поля заряда q2 в точке, где находится q1; т. к. А1 = А2, работу можно записать в виде (§). Из механики: А=DW, W¥ = 0, следовательно, получим: |
|
|
|
электрическая энергия системы из 2-х точечных зарядов. |
2) Система n точечных дискретных зарядов.
Рассуждая аналогично случаю 2-х точечных зарядов, можно получить [17]:
|
|
энергия системы n точечных зарядов (i = 1, 2,…, n) jI – потенциал, создаваемый всеми зарядами, кроме i —го в точке, где находится i –ый заряд, |
3) Заряженный проводник.
Если заряды распределены в теле непрерывно, то суммирование заменяем на интегрирование. Если учесть, что для проводника j = const и использовать выражение для емкости проводника С=q/j, можно получить различные выражения для энергии проводника.
|
|
Энергия заряженного проводника |
4) Заряженный конденсатор.
Рассмотрим две параллельные одинаковые незаряженные пластины, Мысленно перенесем с одной пластины на другую бесконечно малый заряд +dq. Для этого не требуется никакой работы, т. к. пластина пока не заряжена. После этого пластины окажутся разноименно заряженными, и между ними появится разность потенциалов Dj. Для переноса следующей «порции» заряда уже требуется работа dА = dq×Dj = dq×(q/C), где С – емкость конденсатора. Каждая новая «порция» заряда будет повышать заряд q на пластине, и все труднее будет переносить новые порции. Поэтому для вычисления полной работы следует проинтегрировать.
|
Рефераты по физике сдают здесь
Другие статьиУзнать стоимость за 15 минут
Распродажа дипломных
Подпишись на наш паблик в ВК
Нужна работа?
|
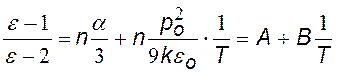
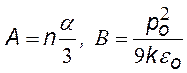
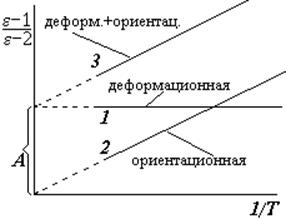 Из формулы следует, что если отложить на графике величину (e — 1)/(e — 2) в зависимости от обратной температуры (1/Т) для различных диэлектриков, то можно получить прямые 1, 2 или 3 (если формула справедлива!). В случае 1 (горизонтальная прямая) мы имеем дело с диэлектриком, у которого молекулы – неполярные. Под действием внешнего поля у таких молекул возникает индуцированный момент, который не зависит от температуры. Измерив величину А, можно вычислить поляризуемость a молекулы. Случай 2 соответствует диэлектрику с ориентационной поляризацией; по наклону прямой можно вычислить собственный дипольный момент р0 молекулы. В случае 3 можно сделать вывод, что молекулы диэлектрика полярные, но под действием поля у них дополнительно возникает индуцированный дипольный момент
Из формулы следует, что если отложить на графике величину (e — 1)/(e — 2) в зависимости от обратной температуры (1/Т) для различных диэлектриков, то можно получить прямые 1, 2 или 3 (если формула справедлива!). В случае 1 (горизонтальная прямая) мы имеем дело с диэлектриком, у которого молекулы – неполярные. Под действием внешнего поля у таких молекул возникает индуцированный момент, который не зависит от температуры. Измерив величину А, можно вычислить поляризуемость a молекулы. Случай 2 соответствует диэлектрику с ориентационной поляризацией; по наклону прямой можно вычислить собственный дипольный момент р0 молекулы. В случае 3 можно сделать вывод, что молекулы диэлектрика полярные, но под действием поля у них дополнительно возникает индуцированный дипольный момент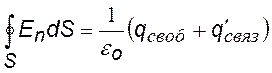 ©
©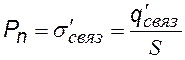
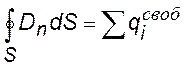
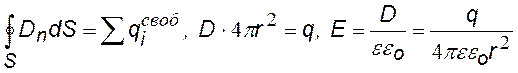
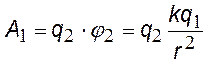
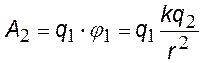
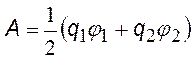 §
§