| Теорема механики об изменении момента количества движения

Вторая – струйная (теория Л. Эйлера). Суть этой теории заключается в том, что сложное движение жидкости внутри рабочего колеса насоса идеализируется и принимается строго упорядоченным – струйным. Для этого рабочее колесо должно иметь бесконечно большое число бесконечно тонких лопастей.

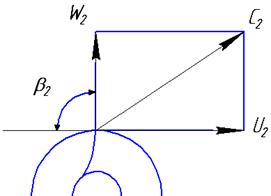
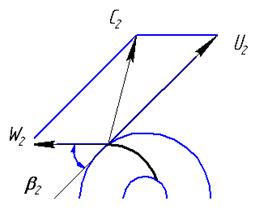
для такого упорядоченного движения жидкости можно представить параллелограммы скоростей на входе и выходе лопастей (рис.10.3) с индексами «1» — на входе и «2» — на выходе. Для этого выделим только одну лопасть (рис.10.3).

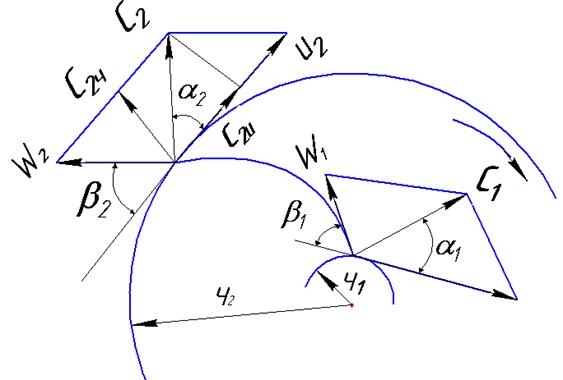
Рис.10.3

При вращении рабочего колеса с угловой скоростью 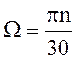жидкость приобретает переносную скорость U, направленную касательно к окружностям радиусов r1 и r2: U = Ωr. При бесконечно большом числе лопастей траектория каждой струйки будет соответствовать профилю лопасти, поэтому под действием центробежной силы каждая частица жидкости относительно и касательно к лопасти приобретает относительную скорость W. Угол между относительной скоростью и обратным направлением переносной скоростью называют углом наклона лопастей β1 и β2.

Для вывода основного уравнения центробежного насоса воспользуемся теоремой механики об изменении момента количества движения для движущейся жидкости, которую в этом случае можно сформулировать так:

Изменение момента количества движения массы жидкости в единицу времени относительно оси вращения рабочего колеса равно сумме моментов всех внешних сил относительно той же оси, т. е. крутящему моменту.

Иллюстрация теоремы представлена на рис.10.4.

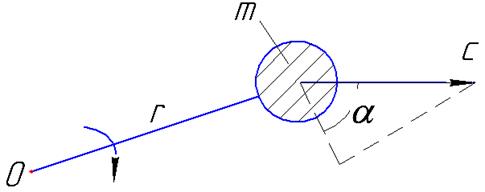
Рис. 10.4

В потоке жидкости, сходящей с лопастей рабочего колеса центробежного насоса, происходит непрерывное увеличение момента количества движения в результате также непрерывного подвода к жидкости механической энергии от двигателя, вращающего рабочее колесо.

Целью вывода указанного уравнения является получение уравнения напора, развиваемого центробежным насосом.

Рассмотрим элементарную струйку, движущуюся вдоль лопасти рабочего колеса насоса.

Моменты количества движения струйки:

на выходе из колеса

;

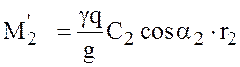на входе в колесо

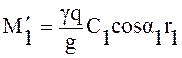Изменение момента количества движения

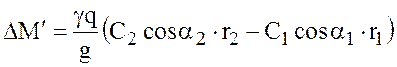Для всей совокупности струек Q = Σq; ΣΔМ` = М. тогда

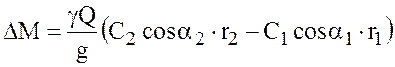Так как 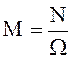; N = ,

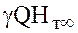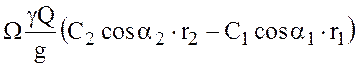Так как Ω·r=U, то

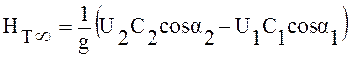. (10.1)

При проектировании центробежных насосов угол α1=90°, т. е. отсутствует предварительная закрутка жидкости; тогда

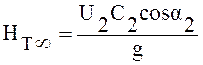. (10.2)

Так как С2·сosα2=C2u, тогда

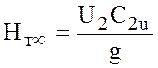. (10.3)

Из параллелограмма скоростей следует, что 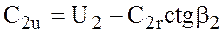; с учетом этого можно записать

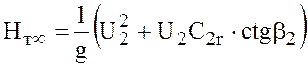. (10.4)

Каждая в отдельности зависимость (10.1, 10.2, 10.3, 10.4) является основным уравнением центробежного насоса, из которого следует основной вывод, что развиваемый напор не зависит от рода перекачиваемой жидкости.

В действительности такой напор насос развить не может, так как число лопастей у реального насоса не бесконечное, а конечное. В этом случае мгновенной передачи механической энергии жидкости не произойдет. Учитывается этот факт коэффициентом ε=0,7…0,9.

Теперь уже в реальном насосе с конечным числом лопастей произойдут гидравлические потери 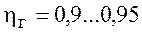вследствие вихреобразования при движении жидкости в рабочем колесе, а также в результате недостаточно плавного входа потока на рабочее колесо (потери на удар при входе) и, наконец, в результате трения жидкости о лопасти и стенки корпуса насоса.

Таким образом, аналитическое выражение действительного напора реально насоса имеет вид

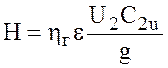. (10.5)

Из уравнений (10.1 — 10.5) следует, что развиваемый центробежным насосом напор зависит в основном от двух факторов: частоты вращения колеса и его диаметра. Для цели получения большего напора тот и другой путь весьма ограничен, поэтому для достижения более высокого напора насосы выполняют многоступенчатыми, когда на одном валу могут быть смонтированы от двух до нескольких сот рабочих колес. Жидкость, поступая от одной ступени к другой, последовательно увеличивает свой напор.

10.1.3. Подача центробежного насоса

Представим схематически рабочее колесо центробежного насоса (рис.10.5).

рабочее колесо насоса наружным диаметром D2 жидкость покидает с радиальной составляющей абсолютной скорости С2r через окна, образованные лопастями шириной b2.

С учетом уменьшения (стеснения) лопастями пространства между дисками колеса теоретическая подача

QT=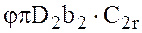, (10.6)

где — коэффициент загромождения, учитывающий толщину лопастей, =0,87…0,92.

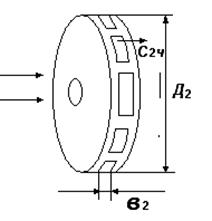
Рис.10.5

Действительная подача с учетом объемных потерь будет несколько меньше:

Q=,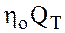

где — объемный к. п.д, =0,95…0,98.

10.1.4. Теоретические характеристики центробежного насоса

Характеристикой насоса называется зависимость напора от подачи при постоянной частоте вращения рабочего колеса:

НТ = f(Q)Т.

Из выражения (10.6) определим радиальную составляющую абсолютной скорости:

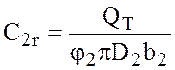
и подставим ее в выражение (10.4):

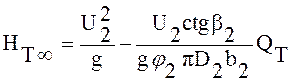. (10.7)

Из выражения (10.7) следует, что теоретическая характеристика центробежного насоса зависит от характера изогнутости лопасти на выходе из рабочего колеса (угол β2) (рис.10.6).

β β2<90о

Наташа

Автор

Наташа — контент-маркетолог и блогер, но все это не мешает ей оставаться адекватным человеком. Верит во все цвета радуги и не верит в теорию всемирного заговора. Увлекается «нефрохиромантией» и тайно мечтает воссоздать дома Александрийскую библиотеку.