Теоремы об изменении количества движения

Систему этих уравнений называют дифференциальными уравне­ниями движения механической системы в векторной форме. Если спроектировать их на оси координат, то получим 3n скалярных диф­ференциальных уравнения.

Мы видели, с какими трудностями приходится сталкиваться при интегрировании дифференциального уравнения движения точки, если сила зависит от времени, положения или скорости. Здесь же мы имеем систему уравнений, и трудности неизмеримо возрастают. По­этому особую роль в динамике системы материальных точек играют общие теоремы, позволяющие в отдельных случаях получить инфор­мацию о характере движения системы без выполнения трудоемкого интегрирования системы дифференциальных уравнений.

3.7. Теоремы об изменении количества движения и

о движении центра масс

Количество движения точки и системы

Количеством движения материальной точки называют вектор, равный произведению массы точки на ее скорость, т. е.

Количество движения точки в физике часто называют импульсом материальной точки. Проекции количества движения точки на декар­товы оси координат

Количеством движения системы называют векторную сумму ко­личеств движения отдельных точек системы, т. е.

Вектор количества движения системы в отличие от вектора коли­чества движения точки не имеет точки приложения. Вектор количе­ства движения точки считается приложенным к самой движущейся точке, а вектор количества движения системы является свободным вектором.

Количество движения системы можно выразить через массу сис­темы и скорость центра масс

если масса системы не изменяется при движении.

Теорема об изменении количества движения системы

Для каждой точки системы, находящейся под действием внеш­них и внутренних сил, имеем:

Проведя суммирование по всем точкам системы, получим:

Используя свойства внутренних сил системы и определение количе­ства движения системы 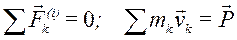, окончательно имеем:

Теорема об изменении количества движения системы: производ­ная по времени от количества движения системы равна вектор­ной сумме всех внешних сил, действующих на систему.

В другой форме теорема выглядит так: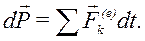

Дифференциал количества движения системы равен векторной сумме элементарных импульсов всех внешних сил, действующих на систему.

Теорема импульсов в конечной (интегральной) форме:

Изменение количества движения системы за какое-либо время равно векторной сумме всех импульсов внешних сил, действующих на систему за то же время.

В проекциях на оси координат

Видно, что внутренние силы не входят в теорему и не влияют на изменение количества движения системы.

Законы сохранения количества движения

Эти законы представляют собой частные случаи теоремы об из­менении количества движения системы.

Если то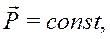

т. е. если главный вектор внешних сил системы равен нулю, то коли­чество движения системы постоянно по величине и направлению.

Если равна нулю проекция главного вектора внешних сил только на одну ось системы координат, то имеем Px=const, то есть проекция количества движения системы на ту же ось является постоянной ве­личиной (сохраняется).

Если мы имеем тело, разрывающееся под действием внутренних сил на две части, то полный импульс системы, состоящей из двух час­тей, сохраняется, то есть:

3.8. Теорема об изменении кинетической энергии

Работа силы.

Элементарная работа силы равна скалярному произведению силы на дифференциал радиус-вектора точки приложения силы (рис.40).

Рис. 40

Элементарная работа силы равна также скалярному произведению элементарного им­пульса силы на скорость точки:

Если сила F перпендикулярна приращению радиус-вектора dr, то элементарная работа силы равна нулю. Полная работ силы:

Другое определение: 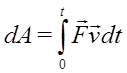, где t=0 соответствует положению точки М0, а момент времени t – положению М.

Последняя формула удобна для вычисления работы силы, когда сила известна как функция времени.

Размерность работы [A]=1Дж=1Н×м.

Мощность. Мощность силы или работоспособность какого-либо источника силы часто оценивают той работой, которую он мо­жет совершить за единицу времени.

Размерность мощности [W]=1Вт=1Дж/с.

Работа силы тяжести

В принятой системе координат (рис. 41 ):

Px=0, Py=0, Pz= − mg.

Работа силы тяжести на перемещении М0М1:

Рис. 41

В системе точек для каждой точки работа Ai=mig(z0i—z1i), полная работа

Работа линейной силы упругости.

Линейная сила упругости действует по закону Гука 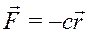, где r – расстояние от начальной точки М0, где сила равна нулю,

до рассматриваемого положения М1, тогда работа

где с – постоянный коэффициент жесткости, λ — деформация (удлине­ние) пружины.

Кинетическая энергия.

Кинетической энергией Т материальной точки называют по­ловину произведения массы точки на квадрат её скорости: T=½ mv2. Размерность кинетической энергии – 1Дж=1Н м.

Кинетической энергией системы Т называют сумму кинетичес-ких энергий всех n точек механической системы, то есть

Вычисление кинетической энергии системы

Разложим движение механической системы на переносное посту­пательное вместе с центром масс и относительное по отношению к системе координат, движущейся поступательно вместе с центром масс.

Запишем связь координат и скоростей точек системы в абсолют­ной (неподвижной) и подвижной системе отсчета:

Выражение для кинетической энергии системы может быть пред­ставлено в следующем виде:

В силу того, что начало подвижной системы отсчета, совмещено с центром масс системы точек