Теория упругости
Исходные данные:
Схема загружения балки-стенки – 3;
l = 18 м; h = 9 м; a = l/3 = 6 м; b = l/3= 6 м; d = 2 м; q = 30 кН/м2; P = 120 кН/м (Рис. 1).
Рис. 1. Схема балки-стенки.
Требуется:
1). Определить значения функции напряжений φ во всех узлах предварительно нанесенной сетки (3х3) методом конечных разностей.
2). Подсчитать напряжения σХ, σУ, τХУ в узловых точках сетки и построить эпюры этих напряжений в одном из вертикальных и в одном из горизонтальных сечений.
3). Сравнить полученное решение (эпюры в вертикальном сечении) с решением теории сопротивления материалов и дать анализ результатов сравнения.
4). Выбрать более густую сетку (6х6) и определить значения функции напряжений в контурных и законтурных узлах.
5). Используя вычислительную программу, подсчитать напряжения σХ, σУ, τХУ в узловых точках сетки и построить эпюры этих напряжений в двух вертикальных и двух горизонтальных сечениях балки-стенки (одно из этих сечений должно совпадать с сечением п. 2).
6). Сравнить полученное решение с результатом «ручного» расчета.
Решение.
Определим реакции (Рис. 2):
Исходя из того, что нагрузка на балку-стенку распределена симметрично, определили
 ;
;
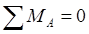 ;
;
RA =330 кН, RB = 330 кН, HB = 0.
Рис. 2. Схема к определению реакций.
Построим эпюры изгибающих моментов (Рис. 3) и продольных сил (Рис.4):
Рис. 3. Эпюра изгибающих моментов.
Рис. 4. Эпюра продольных сил.
Нанесем на балку-стенку сетку 3х3 с шагом Δх = 6 м, Δу = 3 м. Учтем симметрию системы (Рис. 5):
Рис. 5. Расположение узлов сетки.
По формуле запишем функцию φ на контуре балки стенки:
По формуле выразим функцию φ в законтурных точках через внутриконтурные:
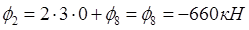
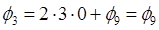
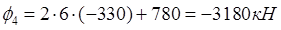
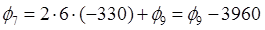
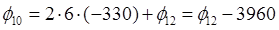
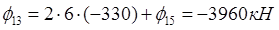
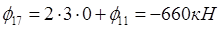
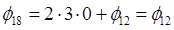
Запишем уравнения для каждой внутриконтурной точки:
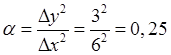
Приведем подобные и получим:
Решая систему находим φ9 = 591,69; φ12 = 269,478
Определим напряжения в узлах сетки и построим эпюры этих напряжений в заданных точках:
Сечение А – А (Рис. 6):
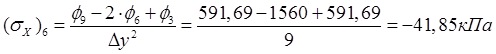 ,
,
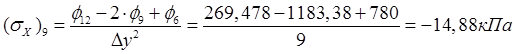
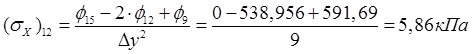 ,
,
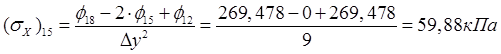 ,
,
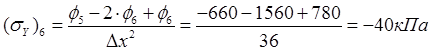 ,
,
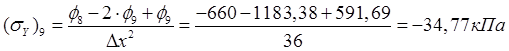 ,
,
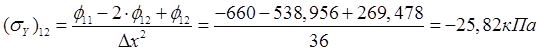 ,
,
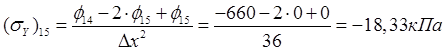 ,
,
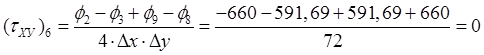 ,
,
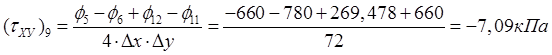 ,
,
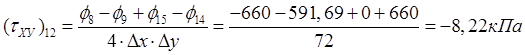 ,
,
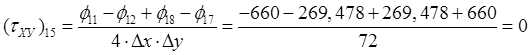 .
.
Сечение В – В (Рис. 7):
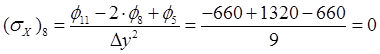 ,
,
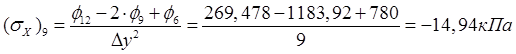 ,
,
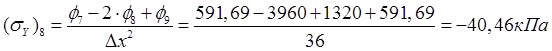 ,
,
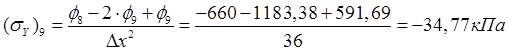 ,
,
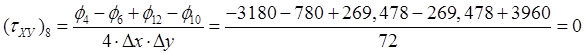 ,
,
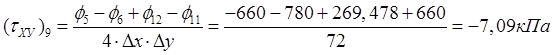 ,
,
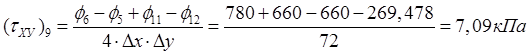 ,
,
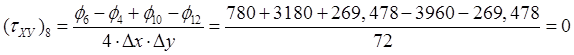 ,
,
Рис. 6. Эпюры напряжений в сечении А – А.
Рис. 7. Эпюры напряжений в сечении В – В.
Построим эпюру σХ в сечении А – А методом сопротивления материалов. Представим балку-стенку в виде обычной балки (Рис. 8):
Рис. 8. Метод сопротивления материалов.
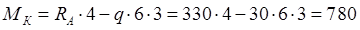 кНм,
кНм,
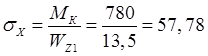 МПа.
МПа.
Эпюра σХ показана на рис. 6 тонкой линией.
Расчет балки-стенки на ЭВМ.
ЧИСЛО УЧАСТКОВ РАЗБИЕНИЯ : ПО ДЛИНЕ — 6,ПО ВЫСОТЕ — 6,ПОРЯДОК СИСТЕМЫ — 25
РАЗМЕРЫ БАЛКИ-СТЕНКИ: ДЛИНА — 15.00 M, ВЫСОТА — 12.00 M
ЗНАЧЕНИЯ МОМЕНТОВ В КОНТУРНЫХ ТОЧКАХ РАМЫ
1) -660.000 2) -660.000 3) -660.000 4) -660.000
5) -660.000 6) -660.000 7) -660.000 8) 195.000
9) 780.000 10) 1095.000 11) 780.000 12) 195.000
13) -660.000 14) -660.000 15) -660.000 16) -660.000
17) -660.000 18) -660.000 19) -660.000 20) .000
21) .000 22) .000 23) .000 24) .000
ЗНАЧЕНИЯ ПРОДОЛЬНЫХ УСИЛИЙ В КОНТУРНЫХ ТОЧКАХ
1) .000 2) -330.000 3) -330.000 4) -330.000
5) -330.000 6) -330.000 7) -330.000 8) -330.000
9) .000 10) .000 11) .000 12) .000
13) .000 14) .000 15) .000 16) -330.000
17) -330.000 18) -330.000 19) -330.000 20) -330.000
21) -330.000 22) -330.000 23) .000 24) .000
25) .000 26) .000 27) .000 28) .000
НАПРЯЖЕНИЯ
Gx Gy Txy
(2.2) .00000E+00 .14667E+03 .10989E+03
(3.2) .00000E+00 -.72874E+02 .11000E+03
(4.2) .00000E+00 -.65774E+02 -.40001E-05
(5.2) .00000E+00 -.54231E+02 .63578E-06
(6.2) .00000E+00 -.42110E+02 .46624E-05
(7.2) .00000E+00 -.33115E+02 .00000E+00
(8.2) -.44000E+03 -.30000E+02 -.99945E+02
(2.3) .18375E+01 -.73333E+02 .00000E+00
(3.3) .13282E+02 -.64623E+02 .13368E+02
(4.3) .88861E+01 -.54157E+02 .18963E+02
(5.3) .11544E+01 -.45340E+02 .19771E+02
(6.3) -.62499E+01 -.38279E+02 .16806E+02
(7.3) -.11761E+02 -.32843E+02 .10195E+02
(8.3) -.12459E+02 -.30000E+02 .55000E+02
(2.4) .73359E+02 .00000E+00 .00000E+00
(3.4) .33583E+02 -.70537E+01 .14952E+02
(4.4) .11178E+02 -.16007E+02 .20276E+02
(5.4) -.47155E+01 -.23711E+02 .21202E+02
(6.4) -.18999E+02 -.29022E+02 .19367E+02
(7.4) -.33893E+02 -.31087E+02 .13845E+02
(8.4) -.47666E+02 -.30000E+02 .00000E+00
(2.5) .88452E+02 .00000E+00 .00000E+00
(3.5) .46287E+02 -.37731E+01 .20345E-04
(4.5) .18466E+02 -.13898E+02 .10173E-04
(5.5) -.10123E+01 -.27667E+02 -.16954E-04
(6.5) -.18765E+02 -.43288E+02 -.22040E-04
(7.5) -.43418E+02 -.59025E+02 -.33908E-05
(8.5) -.91565E+02 -.70000E+02 .00000E+00
(2.6) .73360E+02 .00000E+00 .00000E+00
(3.6) .33583E+02 -.70537E+01 -.14952E+02
(4.6) .11178E+02 -.16007E+02 -.20276E+02
(5.6) -.47156E+01 -.23711E+02 -.21202E+02
(6.6) -.18999E+02 -.29022E+02 -.19367E+02
(7.6) -.33893E+02 -.31087E+02 -.13845E+02
(8.6) -.47666E+02 -.30000E+02 .00000E+00
(2.7) .18376E+01 -.73333E+02 .55000E+02
(3.7) .13282E+02 -.64623E+02 -.13368E+02
(4.7) .88861E+01 -.54157E+02 -.18963E+02
(5.7) .11544E+01 -.45340E+02 -.19771E+02
(6.7) -.62499E+01 -.38279E+02 -.16806E+02
(7.7) -.11761E+02 -.32843E+02 -.10195E+02
(8.7) -.12459E+02 -.30000E+02 .00000E+00
(2.8) -.44000E+03 -.73333E+02 -.10989E+03
(3.8) .00000E+00 -.72874E+02 -.42386E-06
(4.8) .00000E+00 -.65774E+02 -.14438E-05
(5.8) .00000E+00 -.54231E+02 .42386E-06
(6.8) .00000E+00 -.42110E+02 .16954E-05
(7.8) .00000E+00 -.33115E+02 .11000E+03
(8.8) .00000E+00 .19000E+03 .99945E+02
По результатам машинного расчета для примера построены эпюры(рис9,10)
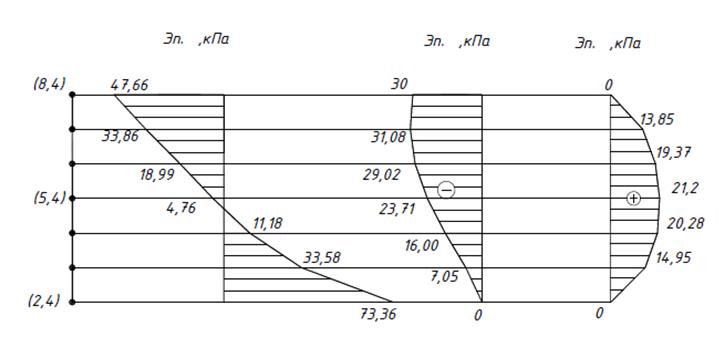
Рис. 9. Эпюры напряжений в сечении А – А.
Рис. 10. Эпюры напряжений в сечении В – В.
Рис. 11. Эпюры напряжений в сечении С – С.
Рис. 12. Эпюры напряжений в сечении D – D.


