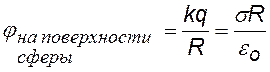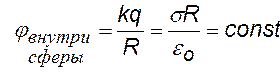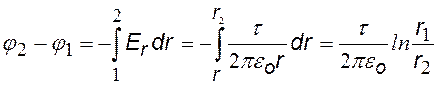Тонкостенный длинный цилиндр
по теореме Гаусса; охватываемый заряд – это отрезок нити длиной l. Приравнивая и сокращая, получим E(r).
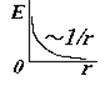
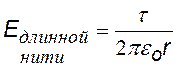
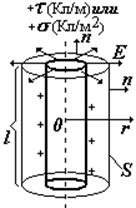
3) Тонкостенный длинный цилиндр, заряженный:
1) с линейной плотностью заряда t или
2) с поверхностной плотностью заряда s.
Этот пример аналогичен предыдущему. Выбираем гауссову поверхность в виде соосного цилиндра, разбиваем поверхность на боковую и две торциальные. В первом случае при заданной линейной плотности t получим такую же формулу, как идля длинной нити. Во втором случае охватываемый заряд равен (s×2p×R×l) и формула для E несколько иная, хотя зависимость от r – та же.
|
|
|
|
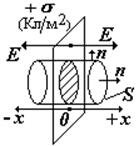
4) Плоскость, бесконечно протяженная, заряженная с поверхностной плотностью заряда s.
Выберем гауссову поверхность S в виде цилиндра, перпендикулярного заряженной плоскости. Высота цилиндра (2×х/2). [9] Разобьем поверхность на боковую и две торцевых.
|
|
поток через Sбок = 0, т. к.× E^n, a = 90о и cosa = 0 |
|
|
|
|
Sзаштрих – площадка с зарядом, охватываемым цилиндром |
||
|
|
|||
|
|
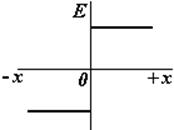
S заштрих = S торц, т. к. образующие цилиндра перпендикулярны заряженной плоскости. Поле протяженной плоскости – однородное и не зависит от расстояния |
|
|
|
|
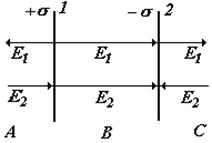
5) Две плоскости, параллельные, разноименно заряженные (плоский конденсатор). В этом случае напряженность поля можно найти по принципу суперпозиции, зная напряженность поля одной плоскости: 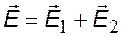
|
|
|
|
|
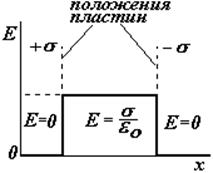
A) ЕА = Е2 — Е1 = 0 B) ЕВ = Е2 + Е1 =s /eо C) ЕС = Е1 — Е2 =0 |
||
|
Поле плоского конденсатора можно считать однородным с достаточной степенью точности, если расстояние между пластинами значительно больше размеров пластин. |
Потенциалы полей различных заряженных тел.
Будем рассматривать только случаи, когда напряженность и потенциал зависят только от одной координаты х или радиальной координаты r для сферически или цилиндрически симметричных тел. Разность потенциалов связана с напряженностью в этом случае как (см. формулу (···)):
|
|
Связь разности потенциалов с напряженностью для случая одной переменной х или r (математически это уравнение однотипно с (···) при замене х® r) |
Из уравнений (ª) или (···) можно найти разность потенциалов, если известна функция Е(r) или Е(r). Чтобы получить формулу для потенциала, следует выбрать уровень нулевого потенциала (так же, как в случае потенциальной энергии – см. механику). Обычно принимают j = 0 на бесконечности, но для поля нити это невозможно (см. ниже).
1) Точечный заряд.
Подставим в формулу (ª) выражение для напряженности поля точечного заряда. 1 и 2 – любые две точки на радиальной оси координат r. Примем j 1 = 0 при
r1 ®¥, заменим j 2 ® j , r2 ®r получим j (r).
|
|
|
|
|
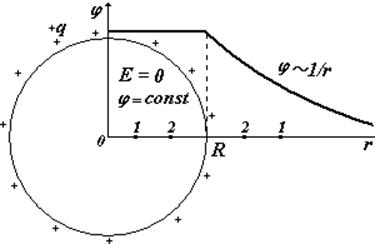
2).Сфера радиуса R, заряженная с поверхностной плотностью заряда s (Кл/м2).
Полный заряд на сфере q = s×4p×R2 . Будем рассматривать две области:1) 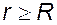 — выбираем две любые точки 1 и 2 в этой области и 2)
— выбираем две любые точки 1 и 2 в этой области и 2) 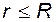 также выбираем две любые точки уже в этой области. Потенциал должен быть непрерывной функцией, в отличие от напряженности он не может иметь разрывов в данной точке, т. к. по смыслу j — потенциальная энергия единичного положительного заряда, а двух энергий у одного заряда в одной точке данного поля не может быть.
также выбираем две любые точки уже в этой области. Потенциал должен быть непрерывной функцией, в отличие от напряженности он не может иметь разрывов в данной точке, т. к. по смыслу j — потенциальная энергия единичного положительного заряда, а двух энергий у одного заряда в одной точке данного поля не может быть.
|
|
Подставим в (ª) Е поля сферы. Для |
|
|
|
|
|
|
|
|
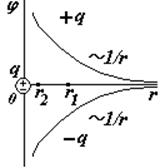
3)Бесконечно длинная нить, заряженная с линейной плотностью заряда t.
Выберем на оси радиальных координат r две любые точки с координатами r1 и r2.
(см. рис.). Подставим в (ª) напряженность поля длинной нити и проинтегрируем.
|
Рефераты по физике сдают здесь
Другие статьиУзнать стоимость за 15 минут
Распродажа дипломных
Подпишись на наш паблик в ВК
Нужна работа?
|
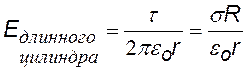
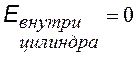

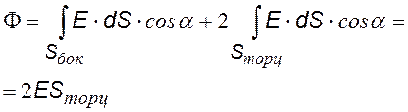
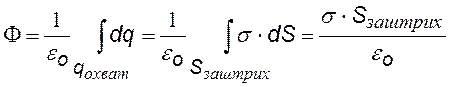
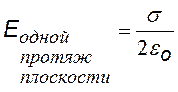
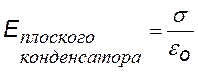
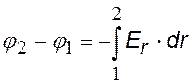 (ª)
(ª)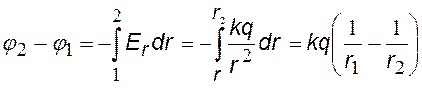
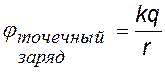 (при j¥ = 0)
(при j¥ = 0)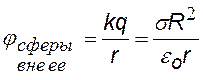 (при j¥ = 0)
(при j¥ = 0)