Условия равновесия произвольной системы сил

Совокупность силы и пары сил и называется динамическим винтом с осью по линии действия .

Вариант 3.3: 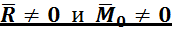, но и не перпендикулярны и не параллельны.

В этом варианте система сил тоже приводится к динамическому винту, но его ось не проходит через центр (рис. 28).

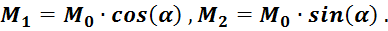
перпендикулярен , значит может быть замена, как в варианте 3.1:

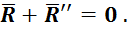
Остаются:

¾  сила 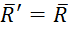в точке на расстоянии от точки ;

¾  момент , как свободный, перенесённый в точку .

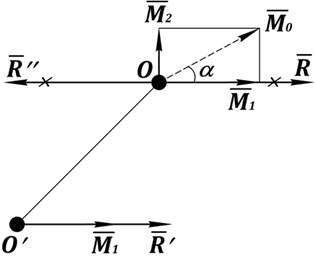
Рис. 28. Приведение пространственной системы сил

к простейшему виду:

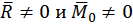, но и

не перпендикулярны и не параллельны

12. УСЛОВИЯ РАВНОВЕСИЯ ПРОИЗВОЛЬНОЙ

(ПЛОСКОЙ ИЛИ ПРОСТРАНСТВЕННОЙ) СИСТЕМЫ СИЛ

Необходимо и достаточно, чтобы было 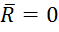, и относительно любого центра было .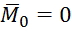

Для пространственной системы сил

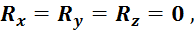
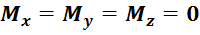
или, используя проекции на оси координат всех сил и их моментов относительно осей

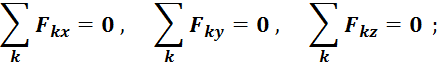
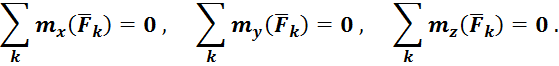
Для плоской системы сил

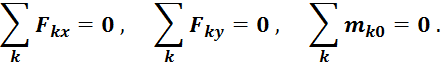
13. ТЕОРЕМА ВАРИНЬОНА

Формулировка: если данная система сил имеет равнодействующую, то момент равнодействующей относительно любого центра равен сумме моментов сил относительно этого центра (рис. 29).

Доказательство:

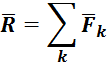
Система сил , , … , заменяется равнодействующей , приложенной в некотором центре .

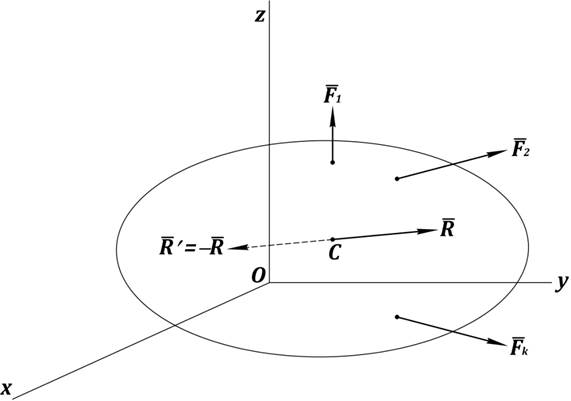
Рис. 29. Теорема Вариньона

Если приложить к центру дополнительную силу 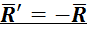, то система будет в равновесии. При этом главный вектор 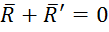, а при равновесии и главный момент относительно центра будет .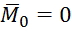

Можно раскрыть содержание величины

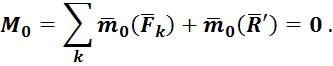
При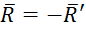

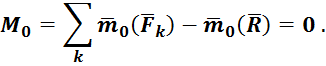
Тогда

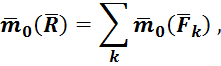
что и требовалось доказать.

14. СЛОЖЕНИЕ ПАРАЛЛЕЛЬНЫХ СИЛ

Условия равновесия тела (рис. 30):