ВУЗы по физике
Готовые работы по физике
Как писать работы по физике
Примеры решения задач по физике
Решить задачу по физике онлайнтуннельный эффект
В процессах поглощения и испускания фотонов атомами должны выполнятся законы сохранения энергии, импульса и момента импульса. Закон сохранения энергии выполняется с помощью частоты поглощенного или испущенного фотона. При поглощении и испускании фотона атом получает импульс отдачи в соответствии с законом сохранения импульса. Поскольку фотон обладает собственным моментом импульса – спином, то в результате поглощения фотона момент импульса атома меняется, что соответствует изменению азимутального квантового числа 
:
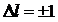. (13.35)
Таким образом, для переходов с участием фотонов должно выполняться условие (13.35), которое называется правилом отбора для процессов поглощения и испускания фотонов атомами.
В классической механике для частицы, на которую действует консервативная сила F(x), выполняется закон сохранения механической энергии – сумма кинетической К и потенциальной U(x) энергии частиц остается постоянной при её движении:
E=K+U(x)=const. (13.36)
Следовательно, для всех положений частицы и любого момента времени справедливо соотношение
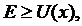(13.37)
поскольку кинетическая энергия является неотрицательной величиной. Область, где E<U(x), запрещена для нахождения частицы законом сохранения энергии.
Согласно законам квантовой механики энергия частицы есть характеристика стационарного состояния и не может быть точно определена в какой-либо момент времени для некоторой точки пространства. Закон сохранения механической энергии (13.36) принимает вид
E=<K>+<U>, (13.38)
где усреднение производится с помощью волновой функции ψ рассматриваемого стационарного состояния:
<K>= <U>= . (13.39)
В результате условие (13.35) заменяется более слабым
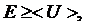(13.40)
поскольку среднее значение потенциальной энергии может оказаться меньше её значений в некоторой области, где U(x)>E. Благодаря этому ослаблению запрета квантовое движение частицы возможно и в тех областях пространства, где соотношения (13.37) не выполняется.
Допустим, что частица массой m с энергией E и импульсом 
движущаяся в положительном направлении оси x, встречает на своём пути потенциальный барьер прямоугольной формы, имеющий высоту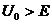 
и ширину 
(рис.13.2). Волновая функция налетающей на барьер вся функция частицы есть волна де Бройля
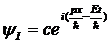, (13.41)
где c — комплексная постоянная и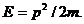 
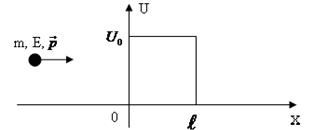
Рис.13.2
Решение стационарного уравнения Шредингера показывает, что несмотря на то, что энергия частицы E меньше высоты 
потенциального барьера, частица может пройти через барьер и оказаться в области x>, где её движение снова описывается волной де Бройля
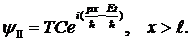(13.40)
Здесь Т — амплитудный коэффициент прохождения потенциального барьера, определяющий вероятность 
прохождения потенциального барьера по средствам выражения
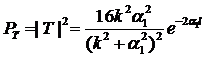. (13.41)
Здесь
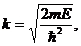
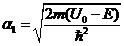
и предполагается, что 
Данное явление прохождения частицы через потенциальный барьер, высота которого превышает энергию частицы, называется туннельным эффектом.
Вероятность туннельного эффекта очень быстро уменьшается с увеличением массы m частицы, разности энергий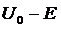 
и ширины барьера 
, поэтому он наблюдается в основном для электронов и нуклонов на пространственных масштабах порядка 
и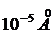 
соответственно. В частности, 
— распад атомного ядра происходит благодаря туннельному эффекту.
В зондовой микроскопии, используемой в современных нанотехнологиях, для анализа поверхностных структур проводящих тел применяется туннельный ток, протекающий между зондом и поверхностью тела. Для получения электронного туннельного тока между зондом с радиусом закругления ~0,1 мкм и поверхностью тела создают постоянное электрическое поле ~1010 В/м, позволяющее электронам преодолеть потенциальный барьер на границе проводника.
Если энергия частицы Е превышает высоту по потенциального барьера 
, то возможно новое квантовое явление — надбарьерное отражение частицы. Частица, отражённая от потенциального барьера, описывается волной де Бройля
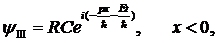(13,42)
распространяющейся в отрицательном направлении оси x. Здесь R-амплитудный коэффициент отражения, определяющий вероятность 
отражения частиц от потенциального барьера
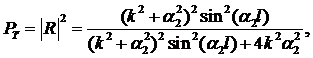(13.43)
и
.
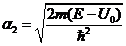Максимальное отражение наблюдается для частиц с энергией
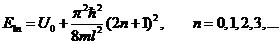, (13.44)
когда вероятность отражения
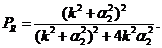(13.45)
В случае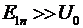 
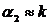и для налетающих частиц со сколь угодно большой кинетической энергией имеется вероятность отразиться от потенциального барьера.
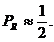(13.46)
МГМИМО
Скидка 30% по промокоду Diplom2020
Получи промокод на скидку 20%
Заказать дипломную работу