Вариационный принцип гамильтона в теории поля

Первая пара получается тривиально с точки зрения СТО.

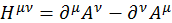(3.1.1)

Возьмем производную от этого выражения:

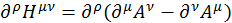(3.1.2)

Используя циклические перестановки индексов, получим:

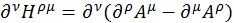(3.1.3)

Теперь сложим уравнения (3.1.2) и (3.1.3). Т. к. смешанные производные по соответствующим компонентам равны, то при сложении уравнений эти шесть членов вместе дают ноль. Таким образом, получаем первую пару уравнений Максвелла:

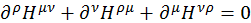(3.1.4)

Найдем уравнение в векторной форме. Для этого проставим индексы и, используя тензор электромагнитного поля, запишем это уравнение в компонентах этого тензора.

Пусть µ=1, ν=2, ρ=3. Получим:

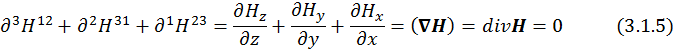
Пусть теперь µ=1, ν=2, ρ=0. В таком случае получаем:

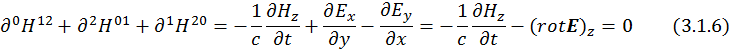
С учетом и первая пара уравнений Максвелла в векторной форме запишется следующим образом:

Обычно эти уравнения выводят из уже известных нам выражений:

Умножим первое уравнений из скалярно на , а второе — векторно на. Тогда получим ту же пару уравнений:

§ 3.2. Вариационный принцип Гамильтона в теории поля

Чтобы найти уравнение движения электромагнитного поля, надо использовать вариационный принцип Гамильтона для поля. Этот принцип гласит: вариация действия для истинного движения равна нулю. Но поле, в отличии от частиц, представляет собой принципиально иную физическую сущность. Если точечные частицы характеризуются своим положением только в одной точке, то поле непрерывно заполняет собой все пространство. В связи с этим и действие, которое для частицы имело вид

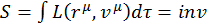(3.2.1)

в теории поля нуждается в переопределении. Для описания поля требуются непрерывные в пространстве и времени величины. Поэтому вместо мы будем использовать 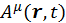. Вместо же 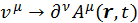, которая является производной по координатам, а не по τ. Сама функция Лагранжа тоже не годится, ее следует заменить на плотность функции Лагранжа 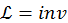. Кроме того, в теории поля . Чтобы действие сохранило свою размерность, произведем замену следующим образом: 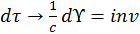. Проверим, выполнится ли это. Размерность действия в теории частиц:

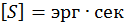(3.2.2)

Подставим размерности для действия в теории поля. Тогда

Следовательно, этот размерный множитель подходит.

Запишем действие (3.2.1) в новых обозначениях:

Чтобы получить уравнение движение мы должны взять вариацию и приравнять ее к нулю:

Рассмотрим более подробно второй член:

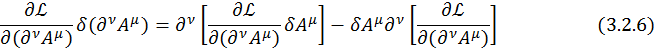
Используя теорему Остроградского-Гаусса, перейдем от интегрирования по четырехмерному объему к интегрированию по замкнутой поверхности.

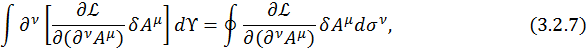
где – четырехмерная гиперповерхность. Размерность её .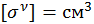

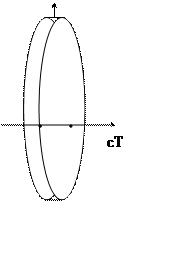Поверхность этой шайбы будет нашей гиперповерхностью в четырехмерном пространстве, если мы возьмем ось симметрии за cT. Все четыре оси должны быть ортогональными. Будем считать, что на боковых гиперплоскостях вариации потенциала

Интеграл по гиперцилиндрической поверхности обратится в нуль, если мы распространим ее на бесконечность, где поля обращаются в нуль. Таким образом, весь наш интеграл по замкнутой поверхности обращается в нуль. Следовательно, выражение 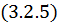перепишется следующим образом:

Чтобы уравнение (3.2.9) всегда обращалось в ноль, нулю должно быть равно выражение, которое стоит в фигурных скобках, т. к. .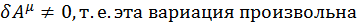

Это и есть уравнение Эйлера-Лагранжа для поля.

Примечание: Оказывается, что имеет произвол, а именно: она определена с точностью до четырехмерной дивергенции от функции произвольных координат и времени. Например, заменим на 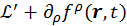. Эта добавка не меняет уравнение Эйлера-Лагранжа, т. е.: