Виды сил трения скольжения

4. Законы трения:

А) Сила трения Fтр направлена в сторону, противоположную относительной скорости скольжения

Б) Сила трения не зависит от площади контактирующих поверхностей

В) Модуль силы трения пропорционален нормальному давлению (чем больше нормальное давление, тем больше сила трения).

5. По рисунку:

А) сила тяжести mg – вниз (чем больше mg, тем больше опорная реакция N (вектор)

Б) тело движется вниз = сила трения направлена вверх по наклонной плоскости

В) гладкая поверхность = опорная реакция N (вектор) направлена перпендикулярна плоскости

Г) по аксиоме 3 строим диагональ параллелограмма R (равнодействующая)

6. Виды сил трения скольжения:

А) сила трения при покое Fтр foN

Б) сила трения при движении Fтр fN

N – сила нормального давления

fo – коэффициент трения покоя

f – коэффициент трения скольжения – зависит от скорости скольжения тел.

Оба коэффициента зависят от материала и физического состояния поверхностей

7. Трение качения – сопротивление, возникающее при качении одного тела к другому.

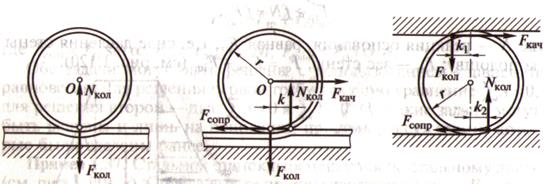
8. Виды связей:

А) идеальные (без трения)

Б) реальные (с трением)

Самостоятельная работа обучающихся – 3час эзс, 4час арх,

1. Решить задачи по определению опорных реакций для однопролётной балки по вариантам

2. Решить задачи на определение усилий в стержнях фермы по вариантам

3. Сравнить способы определения усилий, сделать краткий анализ о преимуществах и недостатках каждого метода — результат оформить в виде таблицы

Авто – 2час

1. Выполнение расчётно­-графической работы на определение опорных реакций балочных систем

ТЕМА 1.5. (ТЕМА 1.6.АВТО) ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ

(эзс – 1 час, арх – 2 час, авто – 1 час)

1. Пространственная система сил – система сил, линия действия которых имеют любые направления в пространстве.

2. Равнодействующая пространственной системы трёх сил, сходящихся в одной точке:

А) приложена в той же точке

Б) равна по модулю и направлению – диагонали параллелепипеда, рёбра которого равны и параллельны заданным силам.

3. Равнодействующая пространственной системы любого числа сходящихся сил равна замыкающей стороне многоугольника, стороны которого равны и параллельны заданным силам (правило силового многоугольника)

4. Условие равновесия пространственной системы сходящихся сил:

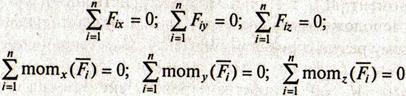
5. Теорема Вариньона:

Момент равнодействующей произвольной плоской системы сил

относительно любой точки равен

алгебраической сумме моментов слагаемых сил системы

относительно той же точки.

(Пример: 5 сил имеют одну равнодействующую силу.

Момент равнодействующей силы = момент первой силы + ….+ момент пятой силы )

Самостоятельная работа обучающихся по теме 1.5.

1. Изучить самостоятельно тему «Аналитическое выражение для определения главного вектора и главного момента», составить опорный конспект — (эзс – 1 час, арх – 2 час)

1. Решение задач на определение момента силы относительно оси пространственной системы произвольно расположенных сил — (авто – 1 час)

ТЕМА 1.6. (ТЕМА 1.7.АВТО) ОПРЕДЕЛЕНИЕ ЦЕНТРА ТЯЖЕСТИ

(эзс – 1 час, арх – 2 час, авто – 1час)

1. Центр тяжести твёрдого тела:

А) Силы притяжения отдельных частиц тела направлены к центру земли.

Б) Эти силы считают параллельными, т. к. размеры тел малы по сравнению с радиусом земли.

В) Равнодействующая этих параллельных сил, равная их сумме – есть вес тела.

Г) Центр тяжести тела — центр этой системы параллельных сил, в котором приложен вес тела.

2. Способы определения центра тяжести:

2. Способы определения центров тяжести

А) способ разбивки на фигуры, положение центров тяжести которых известно.

Б) способ дополнения – частный случай способа разбивки, также разбивка на фигуры с известными центрами тяжести, но некоторые фигуры представляют из себя пустоты.

В) экспериментальный способ – подвешивания, взвешивания

3. Определение координат центра тяжести плоских и пространственных фигур. Центр тяжести лежит

А) у симметричных плоских фигур (с одной осью симметрии) — на оси симметрии («маечка»)

Б) с двумя осями симметрии — на их пересечении (квадрат, прямоугольник)

В) центр тяжести объёмной фигуры (тела) с одной осью симметрии – на плоскости симметрии (найти 2 координаты – по У и Z, по оси Х =0). Пример: ступенька.

Г) при центральной симметрии на оси –в центре симметрии.

Д) для определения центра тяжести симметричных и несимметричных фигур (тел) применяют формулы координат центра тяжести.

4. Устойчивость равновесия (для авто). Разновидности равновесия:

А) устойчивое: при выведении из которого тело возвращается в прежнее положение (шарик на вогнутой поверхности)

Б) неустойчивое: при выведении из которого тело не возвращается в прежнее положение, а удаляется от него ещё больше (шарик на выпуклой поверхности)

В) безразличное (нейтральное) – если при любом смещении его равновесие не нарушается (шарик на ровной поверхности)

5. Условие устойчивости (авто): если центр тяжести тела занимает самое низкое положение по сравнению со всеми возможными соседними положениями, то равновесие тела устойчивое

Самостоятельная работа студентов (эзс – 1 час, арх – 2 час, авто – 1час)

1. Подготовить приложение для решения задач «Сортамент профилей» — используя учебник или сайт, результат оформить в виде сборника таблиц – эзс, арх

1. Решение задач на определение центра тяжести плоских гео­метрических фигур и сечений, составленных из стандартных прокатных профилей – авто

ТЕМА 1.7 УСТОЙЧИВОСТЬ ПОЛОЖЕНИЯ РАВНОВЕСИЯ

(эзс – 1 час, арх – 2 час, авто – нет)

1. Виды потери устойчивости:

А) потеря устойчивости положения: при опрокидывании и при сдвиге

Б) потеря устойчивости формы

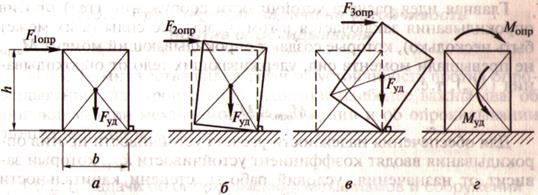
К рисунку:

а) сила F1опр стремится опрокинуть тело, а Fуд (вес тела) удерживает его в первоначальном положении

б) F2опр F1опр – тело может оторваться от плоскости, но при удалении опрокидывающей силы тело возвращается в первоначальное положение силой Fуд (вес тела)

в) F3опр F2опр – при увеличении силы наступает предельное состояние: тело или возвращается в первоначальное состояние, или опрокидывается

г) переход тела в состояние опрокидывания и усиление эффекта опрокидывания

Вывод: в большинстве практических задач ставится требование:

А) о недопустимости опрокидывания

Б) отрыва от плоскости

В) обеспечение запаса удерживающих сил против отрыва

2. Главная идея расчёта устойчивости сооружений (тел) против опрокидывания:

все силы, создающие опрокидывающий момент Мопр,

не должны превышать момента сил,

удерживающих тело от опрокидывания (Муд).

Мопр Муд

3. Коэффициент устойчивости kуст

А) применяют для обеспечения надёжности расчёта устойчивости против опрокидывания

Б) зависит от назначения, условий работы, степени капитальности сооружения или механизма.

В) всегда больше 1, чаще 1,5…2 — т. е. момент Муд должен быть в 1,5-2 раза больше Мопр

4. Условие устойчивости

Муд = kуст Мопр или

Муд = (1,5…2)Мопр

5. Типы задач, решаемые с помощью условия устойчивости:

А) тип 1 – проверка конструкции (тела) на устойчивость – при известных величинах сил (опрокидывающих), точек их приложения, размерах тела и т. д.

Б) тип 2 – определение допустимой величины опрокидывающей силы – когда она не известна

В) тип 3 – определение необходимых размеров конструкции, чтобы опрокидывания не произошло.

Самостоятельная работа студентов (эзс – 1 час, арх – 2 час, авто – нет)

1. Решить практические задачи на устойчивость против опрокидывания по вариантам

РАЗДЕЛ 2. СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ

ТЕМА 2.1. ОСНОВЫ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ (4.1. – АВТО)