Виртуальное облако пиона

Вопрос 2. В гелий-неоновом лазере используются трехуровневые переходы атома неона. Под действием электрического разряда атомы неона перебрасываются на самый высокий из трех уровней. В результате столкновения возбужденных атомов неона с атомами гелия неон переходит на следующий, расположенный ниже уровень. Последний переход, который дает лазерное излучение, происходит со среднего уровня на основной. Какие предположения можно сделать о ширинах спектральных линий, соответствующих этим переходам? Что можно сказать о временах жизни используемых возбужденных состояний атома неона?

3. Обменное взаимодействие

3.1 Виртуальное облако пиона

Зависимость энергии притягивающихся двух нуклонов от расстояния между ними описывается формулой потенциала Юкавы:
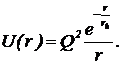(3)
Она вытекает из так называемой обменной модели взаимодействия. Механизм обменного взаимодействия качественно можно понять с помощью принципа неопределенностей.

Рассмотрим обменный механизм адронного взаимодействия протона и нейтрона (механизм связи ядра дейтерия). В этой модели нейтрон рассматривается как связанное состояние протона p и отрицательного пиона p—. Энергия связи пиона и протона почти равна энергии покоя пиона (140 МэВ), поэтому инвариантные массы протона и нейтрона отличаются мало. На пион приходится энергия, почти равная нулю. Тем не менее, принцип неопределенности позволяет пиону пребывать на некотором удалении от протона. Пион, находящийся вне протона, образует виртуальное облако амплитуды вероятности. Виртуальность означает “невозможную возможность”. “Невозможность” относится к тому, что оказавшийся вне протона пион, как и внутри, должен иметь полную энергию, почти равную нулю. Но тогда из выражения энергии
E2=(pc)2+(m0c2)2 (4)
следует, что квадрат импульса отрицательный, что по классическим представлениям невозможно. “Возможность” же означает, что облако дает реально наблюдаемый эффект связи нуклонов.

Если к представлению о виртуальном пионе применить принцип суперпозиции, то виртуальный пион “находится” одновременно в двух состояниях — существует и не существует.

Вопрос 3. Какие экспериментальные факты указывают на то, что энергия виртуального пиона близка к нулю? Чему она равна?

Определим характерный размер виртуального облака пиона. В течение времени Dt энергия системы протон-пион может превышать энергию основного состояния на такую величину DE, что
Dt×DE~ћ. (5)
Понятно, что неопределенность энергии пиона должна иметь порядок энергии покоя
DE~mpc2. (6)
Соответстветствующая верхняя оценка удаленности пиона от протона, или размера облака rh, равна
rh ~ cDt. (7)

Задача 3. Рассчитайте среднее время, в течение которого нейтрон находится в состоянии “протон + пион”.

Из уравнений (5) — (7) следует верхняя оценка размера облака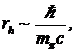
(8)
что совпадает с формулой для радиуса обменного взаимодействия.

3.2 Обменный механизм притяжения

Теперь остается выяснить, как из обменной модели получается притяжение. В изолированном нейтроне размер области локализации пиона равен rh. С малой величиной размера связана большая неопределенность импульса и большая кинетическая энергия. Если к нейтрону приближать протон, то при малых расстояниях между ними у пиона появляется возможность оказываться около другого протона (при этом протон-сосед превращается в нейтрон). Это обстоятельство означает, что размер области локализации пиона при сближении нуклонов увеличивается. Чем ближе нуклоны, тем больше шанс пиону перескочить от одного к другому нуклону. Размер области локализации растет при сближении нуклонов. Неопределенность импульса пиона убывает, а с нею убывает и кинетическая энергия. Можем заключить: чтобы удалить нуклоны друг от друга, придется увеличить энергию системы, т. е. совершить работу. Из проведенных рассуждений вытекает, что из-за возможности перескока пиона от нуклона к нуклону в системе возникает скрепляющая сила. Частица, создающая виртуальное облако и силу взаимодействия, является частицей-переносчиком взаимодействия. Чем больше инвариантная масса частицы-переносчика, тем меньше радиус взаимодействия. Частицей-переносчиком слабого взаимодействия является дабл-ю-бозон (W–). Его инвариантная масса в 90 раз больше массы протона, т. е. почти в 650 раз больше массы пиона, являющегося переносчиком адронного взаимодействия. По этой причине слабое взаимодействие является более короткодействующим, чем адронное. Радиус слабого взаимодействия имеет порядок 10-18 м.

Вопрос 4. В чем состоит неточность утверждения: “Ядро атома гелия состоит из двух протонов и двух нейтронов”?

Механизм ядерного обменного взаимодействия был открыт японским физиком Юкавой в 1934 г. В то время пионы еще не были известны. Но зато из опытов по рассеянию протонов на протонах и нейтронов на протонах был уже определен радиус адронного взаимодействия. Из развитой Юкавой теории и экспериментальных данных об адронном взаимодействии следовало, что в природе должна существовать частица с инвариантной массой, гораздо большей массы электрона и меньшей протона (средней массы, поэтому ее и назвали мезоном — средним). Экспериментальное подтверждение существования мезонов Юкавы имеет сложную и драматическую историю. Примерно в 1937 году в космическом излучении были открыты частицы с массой, близкой к 200 массам электрона. Естественно, их отождествили с мезонами Юкавы. Дальнейшие исследования этих частиц (теперь они известны под названием мюонов, или мю-мезонов) показали, что они очень слабо взаимодействуют с ядрами, и поэтому не могут быть ответственны за большие ядерные силы. Оказалось, что мюоны являются не мезонами, а лептонами. Частицу переносчик адронного взаимодействия нашли лишь через 10 лет — в 1947 году. С составе космического излучения были обнаружены подходящие частицы — пионы. Их масса близка к 270 электронным массам, они сильно взаимодействуют с ядрами.

Задача 4. Какую минимальную энергию должен иметь электрон, чтобы он мог выбить из нейтрона отрицательный пион?

Вопрос 5. Какие обстоятельства, кроме слабости взаимодействия с ядрами, не позволяют считать, что мюон является переносчиком адронного взаимодействия?

Задача 5. Адронное взаимодействие между нуклонами является суммой вкладов обменных взаимодействий, обусловленных не только обменом пионами, но и каонами и эта-мезонами. Почему при расчетах обычно учитывают только пионный вклад?

4. Домашнее задание

4.2 Решение задач

Задача 1. Ковалентная связь молекулы водорода описывается обменной моделью. В отличие от адронного взаимодействия переносчиком ковалентной связи является не виртуальная частица, а реальный электрон, перепрыгивающий от одного атома водорода к другому. Полагая, что в изолированном атоме водорода электрон локализован в области размером 0,51×10-10 м, оцените энергию ковалентной связи молекулы водорода (работу, которую надо совершить, чтобы разорвать молекулу на атомы). Считайте, что при соединении атомов водорода в молекулу размер области локализации электрона увеличивается вдвое.

Задача 2. Среднее время жизни мюона равно 2,2×10-6 с. С какой точностью (в процентах) можно определить массу мюона?

занятие 2.3.4

взаимодействия

2. Скорость взаимодействия

2.1 Скорость распадов

При изучении радиоактивного распада ядер было выяснено, что число нераспавшихся ядер к моменту времени t описывается законом
(1)
где N0 — число нераспавшихся ядер в момент t=0, T — период полураспада, t=T/ln2 — среднее время жизни ядра.

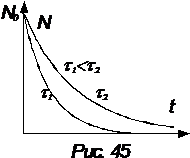Закон изменения числа нераспавшихся частиц N(t) обладает рядом свойств: график имеет вид монотонно спадающей с течением времени функции; за равные промежутки времени число нераспавшихся частиц убывает в одно и то же число раз; график идет тем круче, чем меньше среднее время жизни. Еще одно свойство заслуживает особого внимания. Из формулы (1) следует, что
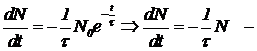(2)
— скорость изменения числа нераспавшихся ядер в момент времени t пропорциональна самому числу ядер.

Опыт показал, что закон распада радиоактивных ядер является универсальным. По этому же закону убывает число нестабильных элементарных частиц одного и того же сорта. Удивительно, но закон работает и при чрезвычайно малых временах жизни частиц.

При больших числах частиц величина N(t)/N0 равна вероятности P уцелеть одной частице к моменту времени t. Например, если в момент времени t=0 число частиц равно 100000, а к концу первой микросекунды осталось 30000, то значение вероятности 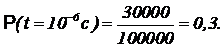Вероятность частице в начальный момент времени уцелеть равна 1. Закон (1) для вероятности выглядит так
(3)
Это общепринятая форма записи закона распада. Из (3) следует P(0)=1. Уравнение, связывающее скорость изменения вероятности и саму вероятность уцелеть согласно (2) имеет вид:
(4)