Внешний фотоэффект

Основными целями настоящей работы являются: экспериментальная проверка уравнения Эйнштейна для внешнего фотоэффекта и определение постоянной Планка методом задерживающего потенциала.

Электроны проводимости в металле

Выход электронов с поверхности вещества под действием света высокой частоты называют внешним фотоэффектом. У большинства металлов фотоэффект происходит в области ультрафиолетового излучения, но для щелочных металлов и их сплавов фотоэффект можно наблюдать даже в видимом диапазоне.

Любой металл содержит очень большое число электронов проводимости. Электроны проводимости обусловливают высокую электропроводность металлов и ряд других физических свойств.

Ряд важных свойств металлов успешно объясняется в рамках приближения среднего поля. В этом приближении действие на отдельный электрон всех остальных электронов рассматривается как внешнее воздействие со стороны этого среднего поля. Полная потенциальная энергия электрона Ue(r) включает в себя также слагаемое, описывающее взаимодействие электрона проводимости положительными ионами металла.

Из-за регулярного расположения ионов в пространстве потенциальная энергия внутри металла имеет периодический характер. Пространственный период эффективной потенциальной энергии имеет порядок нескольких ангстрем.

Уравнение Эйнштейна для внешнего фотоэффекта

Минимальная энергия, необходимая для выхода электрона проводимости из металла в окружающую среду называется работой выхода Ab для данного металла. Эта величина совпадает с высотой потенциального барьера на границе металла для электронов с энергией, равной энергии Ферми. Работа выхода существенно зависит от чистоты поверхности металла и не одинакова на разных участках поверхности.

При облучении металла оптическим излучением электрон проводимости может выйти за пределы металла. Согласно квантовой теории, свет представляет собой поток фотонов, каждый из которых обладает энергией

ε= ħω, (1)

где ω – частота света, ħ — постоянная Планка.

Частота света связана с длиной волны излучения в вакууме соотношением

ω=2πc/λ, (2)

где с-скорость света в вакууме.

Когда электрон проводимости поглощает фотон, энергия электрона увеличивается на величину ħω. Если при этом энергия ħω превышает работу выхода, то электрон может покинуть металл. Ясно, что для этого необходима достаточно большая частота излучения.

Электрон, поглотивший фотон и покинувший металл, называется фотоэлектроном.

Кинетическая энергия фотоэлектронов вычисляется с помощью закона сохранения энергии. Максимальная кинетическая энергия фотоэлектрона подчиняется уравнению Эйнштейна для фотоэффекта

ħω=Еmax+ Ab (3)

Заметим, что условие ħω > Ab является необходимым, но не достаточным условием фотоэффекта. Ясно, что для выхода фотоэлектрона требуется, чтобы вектор импульса был направлен к границе металла.

Практическая часть

Зависимость I(U). Мы измерили зависимость напряжения от фототока. Для этого мы использовали излучение ртутной лампы и таким образом исследовали четыре спектральные линии. Результаты представлены в таблице 1.

Таблица 1.Зависимость напряжения от фототока.

По данным эксперимента построили график зависимости I(U) для четырех спектральных линий.

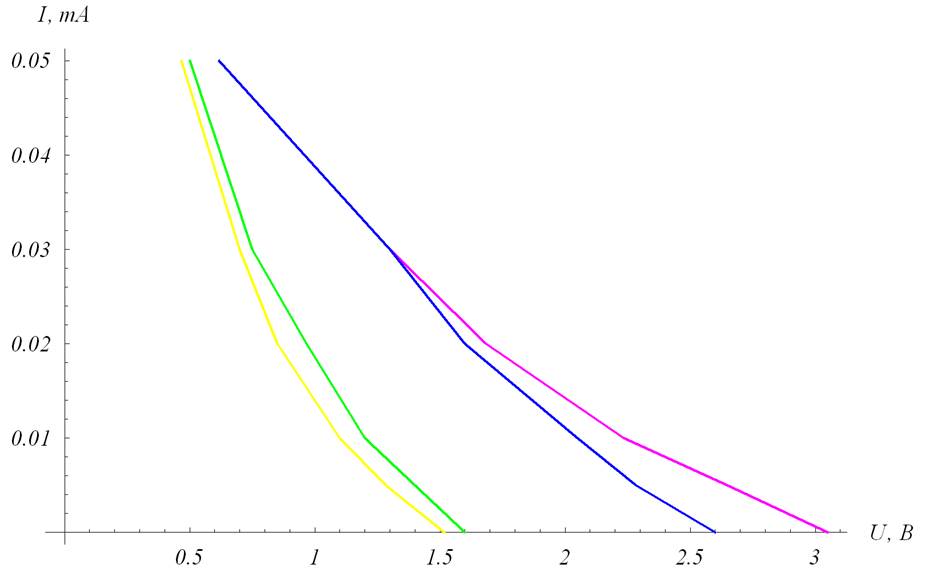
Определим задерживающий потенциал Uo для каждой частоты света ω как абсолютное значение потенциала коллектора, когда фототок равен нулю.

В настоящей работе мы использовали спектральные линии со следующими значениями длин волн:

Желтая-5790,6 Å (ω = 3,255.1015Гц)

Зеленая-5460,7 Å (ω = 3,452.1015 Гц)

Сине-фиолетовая-4358,3 Å (ω = 4,352.1015Гц)

Фиолетовая-4046,8 Å (ω = 4,658 .1015 Гц).

Соответствующие значения потенциала Uo приведены в таблице 2.

Таблица 2. Значения задерживающего потенциала для каждой частоты спектра.

Определим постоянную Планка h и работу выхода Ав методом наименьших квадратов. Зависимость имеет вид: y=ax+b. В нашем случае y=Uo, x= ω, a= ħ /e, b=—Ab/e. Для вычисления коэффициентов используем следующие формулы:

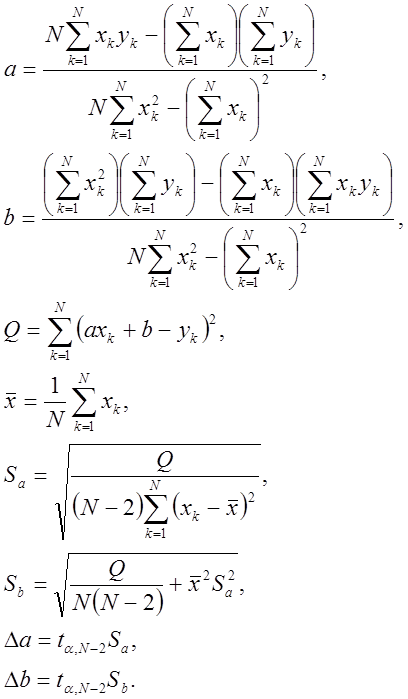
В результате вычислений были получены следующие значения постоянной Планка и работы выхода:

ħ = (1,7±0,7).10-34 Дж. с,

Ав = (3±1) .10-19 Дж.

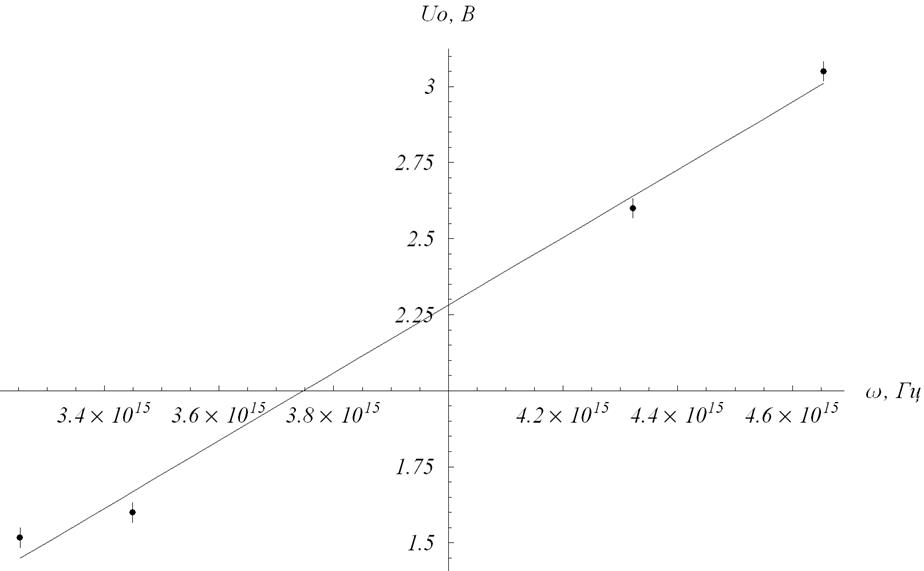
Из уравнения (3) сделаем оценку красной границы фотоэффекта:

ωо=(3±1).1015 Гц.

Выводы:

В ходе данной работы мы экспериментально проверили уравнение Эйнштейна для внешнего фотоэффекта и определили постоянную Планка методом задерживающего потенциала. Теоретическое значение постоянной Планка ħ = 1,1.10-34 Дж. с попадает в доверительный интервал полученного значения ħ = (1,7±0,7).10-34 Дж. с, но не совпадает с ним. Также мы исследовали зависимость величины фототока от напряжения между катодами, изучили зависимость задерживающего потенциала от частоты света, определили работу выхода электронов для сульмяно-цезиевого сплава Ав = (3±1) .10-19 Дж и сделали оценку красной границы ωо=(3±1).1015 Гц.