Волновой пакет

В случае плоской монохроматической волны 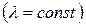, распространяющейся вдоль оси x

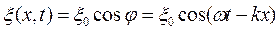, где — амплитуда, — фаза, -циклическая (круговая) частота, t — время, — волновое число (), – расстояние, отсчитываемое в направлении распространения плоскости постоянной фазы =const (волновая поверхность). Они перемещаются в пространстве вдоль направления ОХ со скоростью, получившей название фазовой скорости 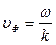. С такой скоростью распространяется синусоидальная волна без изменения своей формы.

Отношение фазовых скоростей в двух различных средах можно определить по отношению показателей преломления, или воспользовавшись законами преломления.

Если среда не обладает дисперсией, то говорить о какой-то другой скорости распространения волны нет необходимости.

Волновой пакет

Строго монохроматическая волна – это идеализация. Таких волн в природе нет. Любая реальная волна, согласно теореме Фурье, может быть представлена как суперпозиция монохроматических волн с различными амплитудами и частотами в некотором интервале частот .

Суперпозицию волн, мало отличающихся друг от друга по частотам (<<) называют волновым пакетом (рис.6-5). В вакууме все монохроматические волны, образующие волновой пакет, распространяются с одинаковой фазовой скоростью. С такой же скоростью распространяется в вакууме и сам волновой пакет, не изменяя своей формы.

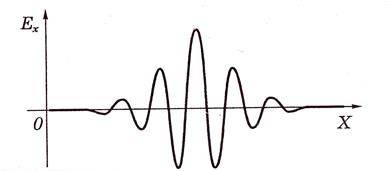
Рис.6-5. Вид волнового пакета в некоторый произвольный момент времени

Групповая скорость

При наличии дисперсии вопрос о скорости распространения волнового пакета становится очень сложным, поскольку скорости его монохроматических составляющих отличаются друг от друга. За скорость распространения волнового пакета принимается скорость перемещения максимума амплитуды волны, рассматривая тем самым максимум в качестве центра волнового пакета (см. рис.6-6). Это, так называемая, групповая скорость. Соответствующий расчет дает, что групповая скорость определяется как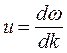

Теоретическое рассмотрение позволяет получить формулу, связывающую групповую и волновую скорости

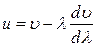
Из этой формулы вытекает, что групповая скорость может быть как меньше, так и больше фазовой скорости, в зависимости от знака .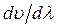

В некоторых случаях групповая скорость оказывается больше значения скорости света в вакууме. Так будет, например, в области аномальной дисперсии. Это не противоречит теории относительности, ибо групповая скорость выражает скорость сигнала лишь тогда, когда волновой пакет не изменяет своей формы в процессе распространения. В области же аномальной дисперсии волновой импульс сильно деформируется, и понятие групповой скорости в таких условиях утрачивает определенное физическое содержание.

Понятие групповой скорости очень важно, так как именно эта скорость фигурирует при измерении дальности в радиолокации, в системах управления космическими объектами и т. д. В теории относительности доказывается, что групповая скорость , в то время как для значения фазовой скорости ограничений не существует.

[1] Название «плоскость поляриза­ции» следовало бы дать не плоскости магнитных колебаний, как это получилось по историческим причинам, а плоскости электрических колебаний.

[2] Открыт в 1810 г. французским физиком Э. Л.Малюсом (1775-1812).

[3] При отражении от проводящей поверхности (например, от поверхности металла) получается эллиптически поляризованный свет.

[4] Изобретена в 1828 г. английским физиком У. Николем (1768-1851).

[5] Д. Керр (1824-1904) — шотландский физик.