Волновые свойства микрочастиц

II. Волновые свойства микрочастиц.

Микрочастицами обычно называют элементарные частицы (электрон, протон, нейтрон и т. д.), также сложные частицы (ядра атомов, атомы, молекулы), образованные из сравнительно небольшого числа элементарных частиц.

1.  Гипотеза де-Бройля.

В 1924 г. Луи де-Бройль (1892-1987гг.), пытаясь найти объяснение постулированным Бором условиям квантования атомных орбит, выдвинул смелую гипотезу, что дуализм не является исключительной особенностью оптических явлений, т. е. электромагнитных волн, а имеет универсальный характер. «В оптике,- писал он,- в течение столетия слишком пренебрегали корпускулярным способом рассмотрения по сравнению с волновым; не делалась ли в теории вещества обратная ошибка?». К этой гипотезе его привела, в частности, аналогия между геометрической оптикой и механикой Ньютона (ещё ранее замеченная Гамильтоном).

Действительно, основные законы оптики и механики представляются в математически тождественной форме: движение частицы в поле с потенциалом 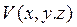можно рассматривать так же, как движение светового луча в среде с соответствующим показателем преломления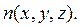

Классическая механика приводит к наилучшим результатам тогда, когда частицу можно рассмотреть как материальную точку и приписать ей определенную траекторию движения. Аналогичная ситуация встречается в оптике, если длиной волны света можно пренебречь по сравнению с другими характерными длинами – это приближение геометрической оптики, когда волновые свойства не проявляются.

Но геометрическая оптика способна описать далеко не все оптические явления, как и механика Ньютона — механические. Может быть, следует расширить аналогию и волновой оптике сопоставить волновую механику?!

Идею волны, заимствованную из оптики, можно перенести в механику вполне последовательно. Однако прежде чем это сделать, следует подчеркнуть нетривиальность попытки объединения волновой и корпускулярной точек зрения.

Действительно, энергия и импульс частицы относятся к точечной, т. е. обладающей пренебрежимо малыми размерами, массе. Напротив, частота и волновой вектор характеризуют бесконечно протяженную во времени и пространстве волну. Трудно представить себе более далекие и несовместимые друг с другом идеи, чем эти две концепции, которые квантовая теория должна объединить в одно целое.

Итак, сначала попробуем развить теорию де-Бройля чисто формально.

Свет Частица

(электромагнитная волна) (например, электрон)

Частота Энергия

Волновой вектор Импульс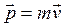

Переход к фотонам Переход к волнам

(гипотеза де-Бройля)

Энергия 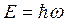Частота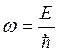

Импульс 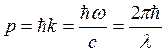Длина волны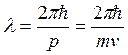

Т. о., движению частицы массой можно сопоставить волновой процесс с длиной волны

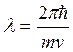, где 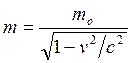. Это волна де-Бройля.

Распространение волн и движение свободных частиц можно описать уравнениями

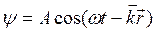
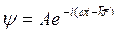
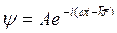
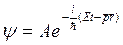
2. Свойства волн де-Бройля.

1)  Фазовая скорость.

Рассмотрим плоскую монохроматическую волну. Уравнение поверхности постоянной фазы

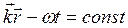. Эта плоскость перемещается вдоль направления волнового вектора с фазовой

скоростью 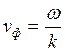. Фазовая скорость электромагнитной волны в вакууме . Для волн, распространяющихся в среде, .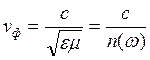

Аналогично, описывая движение частицы, можем найти фазовую скорость волны де-Бройля:

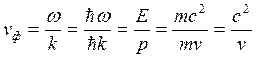, где — релятивистская масса, — скорость частицы.

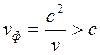, – фазовая скорость волны де-Бройля больше скорости света. Следовательно, фаза волны материи распространяется со скоростью, превосходящей скорость света. Однако в этом нет большой беды. Полученный результат свидетельствует лишь о том, что фазовая скорость не может характеризовать движение физического объекта или передачу информации и в этом смысле лишена определенного физического содержания. Действительно, фазовая скорость есть чисто искусственное понятие, т. к. её нельзя измерить на опыте. Для измерения фазовой скорости необходимо как-нибудь «пометить» определенную часть бесконечной и плавно изменяющейся волны и затем проследить, с какой скоростью будет перемещаться «метка». Единственный способ сделать такую «метку» состоит в том, чтобы в результате интерференции на ранее гладкой волновой поверхности возник какой-либо горб, например, при сложении двух волн с близкими частотами. Таким образом, приходится измерять не фазовую скорость исходной волны, а скорость движения созданного горба. Последняя называется групповой скоростью.

2) Групповая скорость.

Групповая скорость 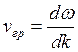– измеряемая величина.

(В разделе “Оптика” § Фазовая и групповая скорость определена из условия постоянства фазы амплитуды огибающей при сложении двух волн с близкими частотами).

Из определения получаем 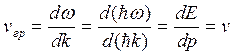– скорость движения частицы.

Действительно, ,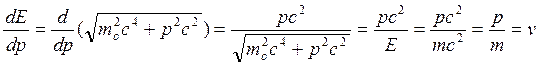

или .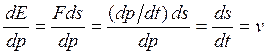

Итак, групповая скорость волн де-Бройля равна скорости движения частицы.

Интересно, что 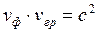.