Волны в среде со слабой пространственной дисперсией
Электромагнитные волны в идеальном диэлектрике и в проводящей среде
4.1. Записать уравнения Максвелла проводящей среде в системе единиц Гаусса и в системе СИ. Пояснить их физический смысл. Вид материальных уравнений в однородной изотропной среде в системе единиц Гаусса и в системе СИ.
4.2. Получить уравнения Максвелла для однородных плоских волн в идеальном диэлектрике. Доказать, что эти волны в идеальном диэлектрике являются поперечными.
4.3. Для плоской электромагнитной волны вывести инварианты одномерных уравнений Максвелла в идеальном диэлектрике. Получить связь векторов ![]() и
и ![]() в волне, бегущей вдоль
в волне, бегущей вдоль ![]() .
.
4.4. Получить выражение для объемной плотности энергии W и вектора плотности потока энергии ![]() электромагнитного излучения. Доказать, что полная энергия в объеме идеальной среды сохраняется. Найти связь W и
электромагнитного излучения. Доказать, что полная энергия в объеме идеальной среды сохраняется. Найти связь W и ![]() в бегущей волне.
в бегущей волне.
4.5. В однородной изотропной проводящей среде вывести волновое уравнение для вектора ![]() и получить дисперсионное соотношение для плоской гармонической волны. Выписать первые три члена разложения
и получить дисперсионное соотношение для плоской гармонической волны. Выписать первые три члена разложения ![]() при
при 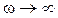 . Найти коэффициент затухания и фазовую скорость.
. Найти коэффициент затухания и фазовую скорость.
4.6. Для плоских электромагнитных волн в проводящей среде вывести формулы для действительной и мнимой частей волнового числа ![]() . Рассмотреть случаи малых и больших частот. Нарисовать графики
. Рассмотреть случаи малых и больших частот. Нарисовать графики ![]() и
и ![]() .
.
4.7. При распространении плоской электромагнитной волны в проводящей среде отношение 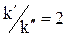 (3,4,5). Чему равен тангенс угла потерь
(3,4,5). Чему равен тангенс угла потерь ![]() ?
?
4.8. В проводящей среде тангенс угла потерь а)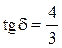 , б)
, б)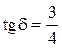 , в)
, в) 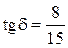 , г)
, г) 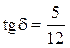 . Чему равно отношение
. Чему равно отношение ![]() ?
?
4.9. Доказать, что в проводящей среде энергия электромагнитного излучения уменьшается со временем.
4.10.Радиоволна с частотой f=0.3 МГц распространяется в земле (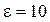 ,
, 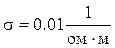 ,
, ![]() ). Определить фазовую скорость и длину волны в земле. Во сколько раз уменьшится напряженность электрического поля на расстоянии 10 м?
). Определить фазовую скорость и длину волны в земле. Во сколько раз уменьшится напряженность электрического поля на расстоянии 10 м?
4.11. Электрические и магнитные свойства воды в океане характеризуются параметрами 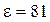 ,
, 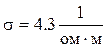 ,
, ![]() . Определить область частот, в которой вода в океане ведёт себя как проводник (
. Определить область частот, в которой вода в океане ведёт себя как проводник (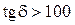 ) и как диэлектрик (
) и как диэлектрик (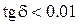 ). Во сколько раз убывает интенсивность волны на глубине 10 м для частот f=
). Во сколько раз убывает интенсивность волны на глубине 10 м для частот f=![]() Гц и f=
Гц и f= ![]() Гц?
Гц?
Волновой пакет в диспергирующей среде.
5.1. В диспергирующей однородной и изотропной среде записать волновое уравнение и получить его общее решение для волнового пакета с медленно меняющейся амплитудой ![]() .
.
5.2. Физический смысл фазовой и групповой скорости, их связь в диспергирующей среде. Что такое нормальная и аномальная дисперсии?
5.3. Найти соотношение фазовой и групповой скорости для электромагнитного сигнала в плазме, если показатель преломления равен 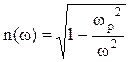 , где
, где ![]() — плазменная частота.
— плазменная частота.
5.4. Найти отношение ![]() и
и ![]() волнового пакета в диспергирующей среде с законом дисперсии а)
волнового пакета в диспергирующей среде с законом дисперсии а) 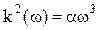 (
(![]() ). Какую размерность имеет коэффициент
). Какую размерность имеет коэффициент ![]() ? б)
? б) 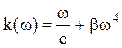 (
(![]() ). Какую размерность имеет коэффициент
). Какую размерность имеет коэффициент ![]() ? в)
? в) 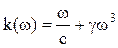 (
(![]() ).Какую размерность имеет коэффициент
).Какую размерность имеет коэффициент ![]() ?
?
5.5. На входе однородной изотропной диспергирующей среды задан волновой пакет с гауссовой огибающей. Найти полуширину его частотного спектра по уровню а) ![]() , б)
, б) ![]() , если начальная длительность волнового пакета
, если начальная длительность волнового пакета ![]() .
.
5.6. В 1-ом приближении теории дисперсии написать дисперсионное соотношение, уравнение для огибающей волнового пакета и его общее решение. Каковы условия применимости 1-ого приближения теории дисперсии? Показать, что в 1-ом приближении теории дисперсии энергия волнового пакета распространяется с групповой скоростью.
5.7. Во 2-ом приближении теории дисперсии написать дисперсионное соотношение, уравнение для огибающей волнового пакета и его общее решение. Каков физический смысл коэффициента диффузии?
5.8. Для волнового пакета с гауссовой огибающей на входе диспергирующей среды 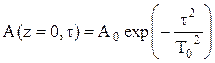 получить решение уравнения для огибающей во 2-ом приближении теории дисперсии. Каковы законы изменения с расстоянием длительности и амплитуды в центре волнового пакета?
получить решение уравнения для огибающей во 2-ом приближении теории дисперсии. Каковы законы изменения с расстоянием длительности и амплитуды в центре волнового пакета?
5.9. Найти во 2-ом приближении теории дисперсии закон изменения с расстоянием амплитуды в центре волнового пакета, если на входе диспергирующей среды задан волновой пакет вида:
а) 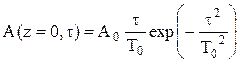 ; б)
; б) 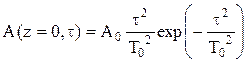 ; в)
; в) 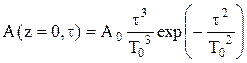 .
.
5.10. Длительность волнового пакета, имеющего гауссову огибающую, увеличивается в 4 раза на длине 10 см. Найти коэффициент дисперсии второго порядка, если начальная длительность волнового пакета ![]() .
.
5.11. Найти минимальный временной интервал между центрами двух волновых пакетов с гауссовой огибающей на входе диспергирующей среды с законом дисперсии 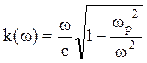 , при котором в точке приема волновые пакеты не перекроются. Прием ведется на расстоянии L=1000 км, несущая частота
, при котором в точке приема волновые пакеты не перекроются. Прием ведется на расстоянии L=1000 км, несущая частота ![]() =3МГц, плазменная частота
=3МГц, плазменная частота ![]() =2.7 МГц.
=2.7 МГц.
5.12. На входе диспергирующей среды задан волновой пакет с гауссовой огибающей и квадратичной модуляцией фазы: 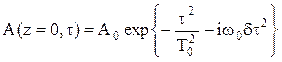 . Найти расстояние, на котором волновой пакет испытывает компрессию.
. Найти расстояние, на котором волновой пакет испытывает компрессию.
Волны в среде со слабой пространственной дисперсией
6.1. Доказать, что в изотропной гиротропной среде бегущих продольных волн нет.
6.2. Показать, что в изотропной гиротропной среде распространяется две нормальные волны с правой и левой круговой поляризацией. Записать дисперсионное соотношение ![]() и вектор
и вектор ![]() для поперечных электромагнитных волн.
для поперечных электромагнитных волн.
6.3. В изотропной гиротропной среде найти точные дисперсионные соотношения для электромагнитных волн с правой и левой круговой поляризацией.
6.4. В изотропной гиротропной среде между нормальными электромагнитными волнами частоты f на длине L сдвиг фаз равен ![]() . Найти константу гирации
. Найти константу гирации ![]() .
.
6.5. Найти угол поворота плоскости поляризации линейно поляризованной плоской электромагнитной волны частоты ![]() , падающей нормально на плоскопараллельный слой изотропной гиротропной среды толщины L (эффект Фарадея).
, падающей нормально на плоскопараллельный слой изотропной гиротропной среды толщины L (эффект Фарадея).
6.6. Для изотропной негиротропной среды получить дисперсионное соотношение ![]() и вектор
и вектор ![]() для продольных и поперечных электромагнитных волн.
для продольных и поперечных электромагнитных волн.
Дифракция квазиплоских волновых пучков.
7.1. Параболическое уравнение в теории дифракции двумерных (круглых) волновых пучков. Физический смысл, условия применимости и общее решение.
7.2. Параболическое уравнение в теории дифракции одномерных (плоских) волновых пучков. Условия применимости и общее решение.
7.3. Для круглого гауссова пучка с первоначально плоским фазовым фронтом получить законы изменения с расстоянием радиуса пучка и амплитуды волны на оси пучка. Чему равны радиус кривизны фазового фронта, угол дифракционной расходимости и фазовый сдвиг на оси пучка в дальней зоне?
7.4. Круглый гауссов пучок радиуса ![]() =1 см на длине волны
=1 см на длине волны ![]() =10 мкм испытывает дифракцию в сводобном пространстве. Определить расстояние, на котором кривизна фазового фронта достигает максимальной величины, и найти радиус кривизны в этой точке.
=10 мкм испытывает дифракцию в сводобном пространстве. Определить расстояние, на котором кривизна фазового фронта достигает максимальной величины, и найти радиус кривизны в этой точке.
7.5. Определить расстояние d, на котором радиус круглого гауссова пучка ![]() =1 см увеличится вдвое. Длина волны
=1 см увеличится вдвое. Длина волны ![]() =10 мкм.
=10 мкм.
7.6. Как меняется фаза поля на оси круглого гауссова пучка с первоначально плоским фазовым фронтом при переходе от ближней к дальней зоне? Нарисовать график ![]() .
.
7.7. Для плоского гауссова пучка с первоначально плоским фазовым фронтом получить законы изменения с расстоянием радиуса пучка и амплитуды волны на оси пучка. Чему равны радиус кривизны фазового фронта, угол дифракционной расходимости и фазовый сдвиг на оси пучка в дальней зоне?
7.8. Для круглого гауссова пучка с первоначально плоским фазовым фронтом получить законы изменения с расстоянием радиуса пучка и амплитуды волны на оси пучка. На расстоянии L от входа в среду найти зависимость интенсивности излучения на оси гауссова пучка от величины входного радиуса пучка ![]() , нарисовать график
, нарисовать график ![]() и найти оптимальный радиус, при котором интенсивность максимальна. Мощность пучка P остается постоянной.
и найти оптимальный радиус, при котором интенсивность максимальна. Мощность пучка P остается постоянной.
7.9. Для сфокусированного гауссова пучка с начальным распределением амплитуды 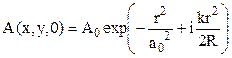 получить законы изменения с расстоянием радиуса пучка и амплитуды волны на оси пучка. Определить фокусное расстояние, радиус фокального пятна и амплитуду в фокусе.
получить законы изменения с расстоянием радиуса пучка и амплитуды волны на оси пучка. Определить фокусное расстояние, радиус фокального пятна и амплитуду в фокусе.
7.10. В дальней зоне найти угол дифракционной расходимости ультразвукового пучка в биологической ткани. Излучатель имеет радиус кривизны R=5 см и несущую частоту f=2 МГц. Скорость звука в биологической ткани 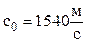 , начальный радиус пучка
, начальный радиус пучка ![]() =1 см.
=1 см.


