Воздействие электромагнитного излучения

К ТЕОРИИ ФИЛЬТРАЦИИ ЖИДКОСТИ В ПОРИСТОЙ СРЕДЕ ПРИ ОБЪЕМНОМ НАГРЕВЕ ВЫСОКОЧАСТОТНЫМ ЭЛЕКТРОМАГНИТНЫМ ПОЛЕМ

Зыонг Нгок Хай. Кутутев А. Г.. Нигматулин Р. И.

Исследуется процесс фильтрации и разогрева очень вязкой жидкости (битума) пористой среде при наличии объемного источника тепла за счет поглощения энергии высокочастотного электромагнитного поля (ВЧЭМП). Эта задача связана с анализом битумных нефтей, фильтрация которых практически реализуется только после предварительного разогрева пласта, например при помощи ВЧЭМП.

Предполагается, что в начальном состоянии битум находится в жидком (подвижном) и твердом (неподвижном) состоянии. Под воздействием объемного источника тепла битум нагревается, плавится, расширяется, становится текучим и под создаваемым перепадом давления движется относительно неподвижного твердого пористого скелета породы. Получена замкнутая система дифференциальных уравнений и устанавливаются основные безразмерные критерии подобия, характеризующие указанные процессы. Изучаются различные типы стационарных или предельных решений, реализующихся при стационарном или достаточно длительном разогреве среды. Эти решения в случае их существования, могут быть использованы для оценки эффективности реального процесса (например, для опенки предельной длины области плавления, степени нагрева жидкого битума и характерного времени выхода процесса на стациионарный режим и т. и.) и в качестве тестов для проверки правильности различных приближенных и численных методов решении полученной системы нелинейных дифференциальных уравнений.

Рассматриваемая задача отличается от классической задачи Стефана о процессах плавления или затвердевания, где предполагается, что среда однокомпонентная, отсутствует движение среды и связанный с ним конвективный перенос тепла, а внешний подвод тепла происходит только на границах исследуемых областей (т. е. объемная источник тепла отсутствует).

1. Основные допущения и уравнения. Процессы разогрева, плавления я фильтрации битума исследуются методами механики многофазных сплошных сред при следующих основных допущениях: температуры фаз в каждом элементарном объеме пористой среды одинаковы; процесс фазового перехода (плавления или затвердевания) происходит на скачке, разделяющем зоны пористой среды, заполненной жилкой не твердой фазами битума (т. е. нет зоны смеси жидкой н твердой фаз битума); движенце расплавленного битума в породе безынерционное и подчиняется закону Дарен; отсутствуют изменение объема нерасплавленной (твердой) фазы и деформация скелета породы. При принятых допущениях рассматриваются основные уравнения сохранения масс, импульсов фаз и энергии смеси для случая одномерного симметричного движения (v — U, 1.2 соответствуют случаям плоской, цилиндрической и сферической симметрии движения) в эй­леровой системе координат.

Примем следующие обозначения. Нижние индексы i = 1, 2, 3 будем относить к параметрам соответственно подвижной (жидкой) фазы битума, неподвижной (твердой) фазы битума и скелета породы; нижний индекс s — к параметрам на линии плавления, а индексы 0, b — к параметрам начального состояния и на границе скважины соответственно. Через ρi, ui, ci, λi обозначим истинную плотность, скорость фильтрации, удельную теплоемкость b коэффициент теплопроводности i-й фазы (i = 1,2,3), р,μ1 — давление к вязкость жидкости, к. т — проницаемость и пористость породы (k, т — const), Т — температура, хь — координата стенки скважины, xc (t) — координата поверхности плавлении. Введем также величины (ρc)(i)=mρici + (1-m) ρ3c3, λ(i)=m λi+(1-m) λ3, m=const, i=1,2. В области подвижной фазы — жидкости (расплавленного битума) xb<x<xs(t), T>Ts. Уравнения сохранения массы, импульса и энергии запишем в виде:

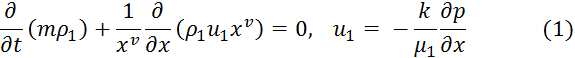
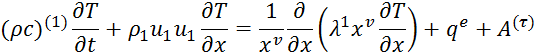
Где — работа вязких сил, — интенсивность объемного источника тепла за счет поглощения энергии ВЧЭМП. Далее будем рассматривать случай, когда ≤, и величиной можно пренебречь. Вязкость жидкости температуры (=(T)).

В области неподвижной фазы твердого битума x>xs(t), t>ts имеем:

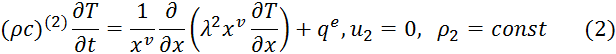
На границах исследуемой области и фронте направления:

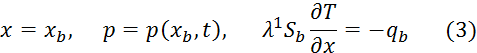
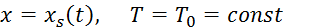
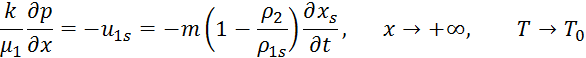
В случае T0<Ts при t<ts распределение температуры среды в области [(xb +) ×[0,ts] с граничными условиями Умова –Пойтинга и закон Бугера-Ламберта для монохроматической волны

Где R – вектор интенсивности излучения, а — длина поглощения, характеризующая степень поглощения электромагнитной волны рассматриваемой средой. В случае распространения одномерной (плоской, цилиндрической и сферической) монохроматические волны в однородной и изотопной среде эти уравнения имеют вид

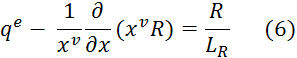
В общем случае для заданной среды длина поглощения определяется частотой электромагнитного излучения ω и зависит от давления р и температуры. Тогда даже при фиксированной частоте ωуравнения для термогидродинамических параметров (1.1) и (1.2) и уравнения (1.6) для и электрофизического параметра R взаимосвязаны и должны решаться совместно. Часто влиянием давления и температуры на длину поглощения можно пренебречь. Тогда для фиксированной частоты ω величина становится заранее известным параметром, который сразу определяет интенсивность излучения R и интенсивность объемного источника тепла независимо от решения термогидродинамических уравнений. Здесь:

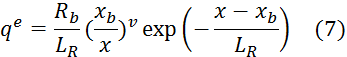
Положение поверхности плавления определяется из условий баланса массы и в квазистатическом (фильтрационном) приближении баланса энергии на межфазной границе

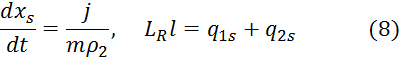
Здесь 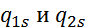— потоки тепла, поступающие к межфазной поверхности со стороны подвижной и неподвижной фазы, j, l – соответственно интенсивность и удельная теплота фазового перехода (разность энтальпий фаз).

Принимаются линейные уравнения состояния для плотности жидкости

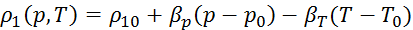
Где 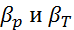— коэффициент сжимаемости и теплового расширения. Тогда система термогидрономических уравнений (1)-( 4), (7)-(9) при заданных начальных условиях t=0, p=p0, T=T0 замкнута и может быть решена.