Вторая пара уравнений максвелла в дифференциальной форме

§ 3.3. Вторая пара уравнений Максвелла в дифференциальной форме для чистого поля

Чтобы получить конкретные уравнения электромагнитного поля, необходимо задать явный вид плотности функции Лагранжа, которая должна быть инвариантной величиной.

Мы выбрали именно этот инвариант, т. к. он дает уравнения, которые удовлетворяют экспериментальным данным. Если бы мы взяли другой инвариант, то получили бы первую пару уравнений Максвелла.

Нам нужно подставить в уравнение Эйлера-Лагранжа:

Для начала вспомним, что

в случае чистого поля не зависит от потенциала, поэтому

Рассмотрим теперь первое слагаемое в формуле :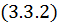

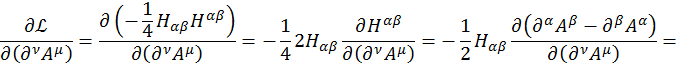
Таким образом, получили вторую пару уравнений Максвелла:

или

Покажем, что это именно пара уравнений, задавая индекс µ. Пусть сначала µ=1:

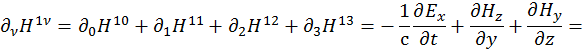
Пусть теперь µ=0:

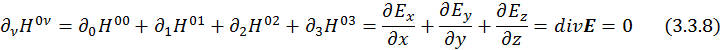
Таким образом, получили два уравнения, выпишем их отдельно:

§ 3.4. Вторая пара уравнений Максвелла в дифференциальной форме при наличии зарядов и токов

Заряды и токи сами могут создавать электромагнитные поля. Обобщим действие с учетом зарядов и токов. Действие – аддитивная величина, следовательно, оно слагается из действий самих зарядов , а также члена, учитывающего взаимодействие зарядов с полем и действия для чистого поля :

где

Будем считать, что мы уже знаем движение зарядов и уравнение движение зарядов. Следовательно, выполняется условие .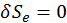

В формуле -потенциал внешнего поля по отношению к зарядам.

Здесь -потенциал, создаваемый самими зарядами; -элемент четырехмерного объема;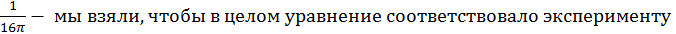

Первый член в формуле 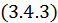написан в терминах частиц, поэтому он не готов для применения в теории поля. Необходимо перейти от 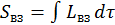к .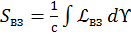

Учитывая, что

выражение примет вид:

Величина 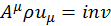, если — четырехмерный вектор. Обозначим:

Тогда эффективное действие будет равно

Зная действие, можно определить плотность функции Лагранжа.

Подставляя это в уравнение Эйлера-Лагранжа(3.2.10), будем иметь

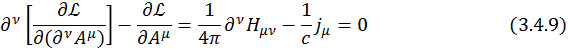
Из выражения видно, что

Таким образом, мы получили вторую пару уравнений Максвелла, которая в явном виде записывается как два уравнения:

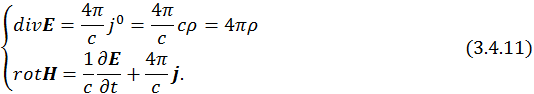
Иногда вместо плотности тока 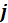вводят плотность тока смещения.

где