Вторая пара уравнений максвелла в интегральной форме
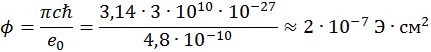
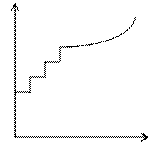
Был проведен эксперимент: кольцо из сверхпроводникового сплава (рис. слева) при очень низких температурах помещено в магнитное поле.
Сверхпроводники являются абсолютными диамагнетиками, т. е. они внутрь себя не пропускают магнитное поле, они его выталкивают, следовательно, в кольце появятся сверхпроводящие токи, которые будут уничтожать внешнее магнитное поле. В этом кольце возникнет много маленьких круговых токов, при сложении которых по внешней стороне кольца пойдет электрический ток, вследствие чего появится магнитное поле сверхпроводника.
|
Н |
Если резко убрать внешнее магнитное поле, то магнитное поле сверхпроводника останется. Если уменьшать магнитное поле медленно, то магнитное поле сверхпроводника будет уменьшаться квантами. Внешнее магнитное поле уменьшается непрерывно, а магнитное поле сверхпроводника – ступенчато. Но даже при полном отсутствии внешнего магнитного поля, магнитное поле сверхпроводника все равно останется, и этот его элементарный поток равен |
§ 3.6. Вторая пара уравнений Максвелла в интегральной форме
Для вывода второй пары уравнений Максвелла в интегральной форме, возьмем пару в дифференциальной форме
![]()
и проинтегрируем её, перед этим умножив на ![]() .Тогда получим:
.Тогда получим:
![]()
где 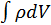 есть полный заряд q. Используя теорему Остроградского-Гаусса, получим:
есть полный заряд q. Используя теорему Остроградского-Гаусса, получим:
![]()
Это и есть первое уравнение второй пары в интегральной форме. Его удобно использовать при решении задач. Уравнение ![]() предполагает существование в природе электрических зарядов, магнитных же зарядов нет. Его можно использовать для простого определения электрического поля, создаваемого отдельными зарядами, находящимися внутри этой самой замкнутой поверхности
предполагает существование в природе электрических зарядов, магнитных же зарядов нет. Его можно использовать для простого определения электрического поля, создаваемого отдельными зарядами, находящимися внутри этой самой замкнутой поверхности ![]() .
.
Возьмем, например, заряд в виде однородно заряженного шарика. Определим электрическое поле ![]() , которое создается этим положительным зарядом. Рассмотрим два случая: электрическое поле вне и внутри шарика.
, которое создается этим положительным зарядом. Рассмотрим два случая: электрическое поле вне и внутри шарика.
Покажем, что вне этого шара, радиуса а, Е будет одинакова для шаров любого радиуса, и будет совпадать с кулоновским полем, а внутри Е растёт пропорционально радиусу самого шарика. Эту зависимость очень просто получить из соотношения (3.6.2).
1. Вычислим напряжённость вне шара, создаваемую им самим.
Из соображений симметрии ясно, что напряжённость электрического поля в каждой точке этой сферы будет одинакова. А вектор нормали k элемента поверхности ![]() будет параллелен радиус-вектору r в каждой точке. Следовательно, при интегрировании напряжённость электрического поля Е = const. Тогда
будет параллелен радиус-вектору r в каждой точке. Следовательно, при интегрировании напряжённость электрического поля Е = const. Тогда
![]()
С другой стороны, согласно (3.6.2)
![]()
Следовательно, напряжённость кулоновского поля вне шара равна
![]()
Это выражение не зависит от размеров шарика. В каждой точке вне шара напряжённость электрического поля описывается кулоновским взаимодействием.
2. Рассмотрим напряжённость внутри шара. На каждой точке сферической поверхности внутри шара напряжённость поля постоянна. Следовательно, её можно вынести за знак интегрирования.
![]()
где 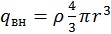 – заряд внутри сферы радиуса r,
– заряд внутри сферы радиуса r, ![]() – объемная плотность заряда,
– объемная плотность заряда, ![]() – объем шарика.
– объем шарика.
Подставляя эти выражения в 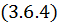 , получаем
, получаем
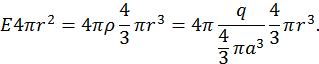
Здесь ![]() – полный заряд, a-радиус шарика. Получаем, что напряжённость внутри шара есть
– полный заряд, a-радиус шарика. Получаем, что напряжённость внутри шара есть
![]()
Построим график зависимости напряженности электрического поля от расстояния. Учитывая то, что внутри шара ![]() ~
~ ![]() , а вне ~
, а вне ~ ![]() , получим следующую зависимость:
, получим следующую зависимость:
|
0 a r |
Теперь рассмотрим другое уравнение (3.4.11) второй пары в интегральной форме. Для этого уравнение в дифференциальной форме
![]()
переведем в интегральное (3.6.7).
![]()
К левой части уравнения (3.6.7) применим теорему Стокса. Тогда, учитывая, что 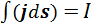 и
и 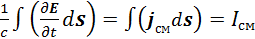 , получим выражение
, получим выражение
![]()
где ![]() – ток смещения,
– ток смещения, 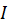 – омический ток, связанный с потерей энергии на тепло в проводниках и движением зарядов.
– омический ток, связанный с потерей энергии на тепло в проводниках и движением зарядов.
Эту формулу можно использовать для определения напряжённости магнитного поля в проводниках.
§ 3.7. Четырехмерный вектор плотности тока
Проблема состоит в том, что в рамках теории поля понятия точечного заряда или заряженной частицы не существует. В ней все физические величины в некотором смысле рассредоточены в пространстве. Но так как объективно понятие точечного заряда существует, необходимо разработать специальный математический аппарат для их описания применительно к теории поля. Согласно (3.4.6) имеем
 Ф
Ф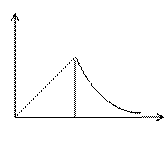 E
E

