Вывод формулы для расчета работы сил поля

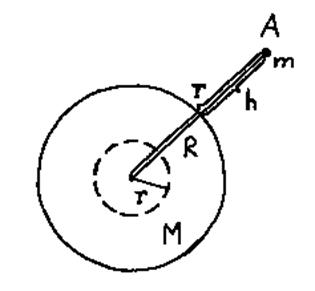
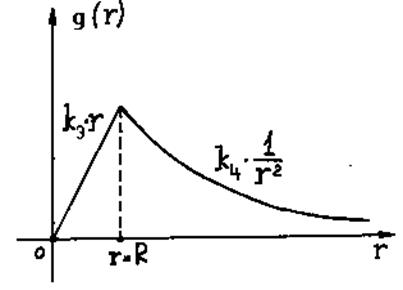
Рис. 3.17. Рис. 3.18.

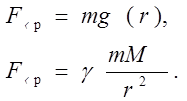
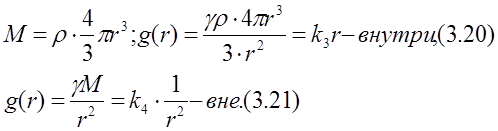
Как вы считаете: случайно ли это совпадение?

Тесты к лекции №3.

Тест 3.1. Дайте формулировку теоремы Остроградского-Гаусса:

£ поток вектора напряженности электрического поля через произвольную замкнутую поверхность равен алгебраической сумме заключенной внутри этой поверхности зарядов, деленной на ε0.

£ поток вектора напряженности электрического поля через замкнутую поверхность равен 0.

£ поток вектора напряженности электрического поля через замкнутую поверхность равен алгебраической сумме зарядов, заключенных внутри этой поверхности.

£ поток вектора напряженности электрического поля через замкнутую поверхность равен алгебраической сумме заключенной внутри этой поверхности зарядов, умноженной на ε0.

Тест 3.2. Какой формулой описывается поле заряженной нити?

£

£

£

£

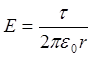
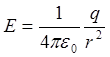
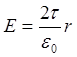
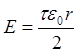
Тест 3.3. Чему равен суммарный поток, создаваемый при пересечении линиями напряженности “морщин”?

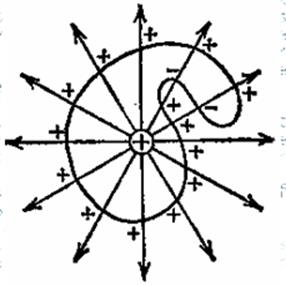
£ 1.

£ -1.

£ 0.+

£ q.

£ –q

Тест 3.4. Поверхностная плотность заряда выражается формулой:

£

£

£

£

£

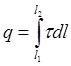
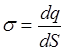
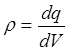
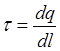
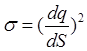
Тест 3.5. Объемная плотность заряда выражается формулой:

£

£

£

£

£

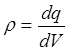
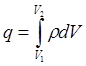
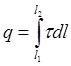
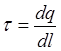
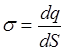
Работа электрического поля по перемещению заряда. Потенциал. Потенциальный характер электростатического поля[11]

4.1. Вывод формулы для расчета работы сил поля при перемещении заряда.

4.2. Понятие потенциала, потенциальный характер электростатического поля.

4.3. Связь между напряженностью и потенциалом.

4.4. Потенциал поля плоского конденсатора, заряженной нити, цилиндрического и сферического конденсаторов.

4.1. Вывод формулы для расчета работы сил поля при перемещении заряда

Пусть имеется точечный положительный заряд. Рассчитаем работу по его перемещению из точки 1 в точку 2.

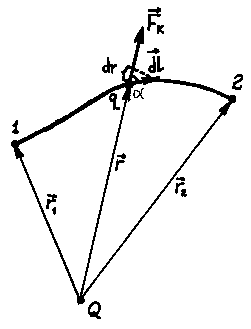
Рис. 4.1.

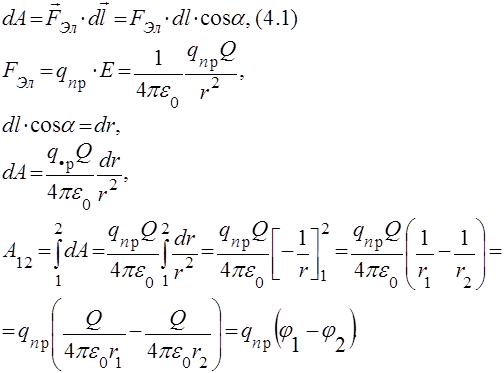
Вывод: работа по перемещению заряда из одной точки поля в другую равна произведению величины этого заряда на разность потенциалов начальной и конечной точек траектории.

4.2. Понятие потенциала, потенциальный характер электростатического поля

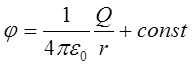
может служить характеристикой поля.

Т. к. при 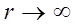функциональная часть выражения (4.2) , то примем const = 0. Получим:

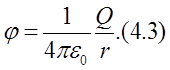
Эта величина получила название: потенциал поля точечного заряда:

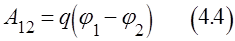
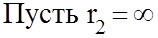, тогда 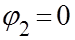и

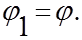
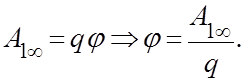(4.5)

Потенциалом поля в данной точке называется физическая величина, численно равная работе по переносу единичного положительного заряда из данной точки поля в бесконечность.

Работа сил электростатического поля равна убыли потенциальной энергии, т. е.:

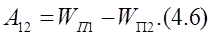
Тогда, сравнив (4.4) и (4.6), получим:

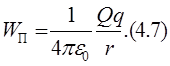
Т. к. при 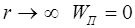, то :

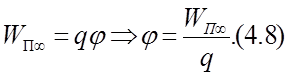
Потенциалом поля в данной точке называется физическая величина, численно равная потенциальной энергии, которая приобретается единичным положительным зарядом при переносе его из бесконечности в данную точку поля.

Выясним свойства потенциального электростатического поля.

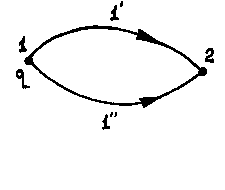
Рис. 4.2.

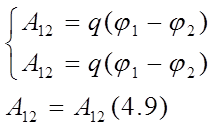
1. Работа по переносу заряда из одной точки электрического поля в другую не зависит от формы траектории.

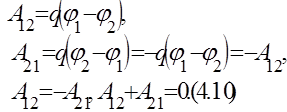
2. Работа по переносу заряда вдоль замкнутой траектории равна нулю.

,
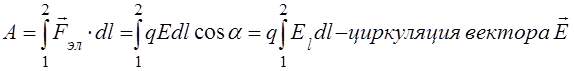
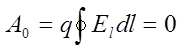