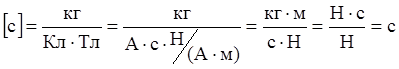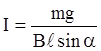Задача на применение закона био-савара-лапласа
Проведем проверку размерности:
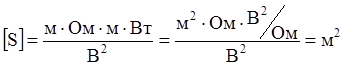
Произведем вычисления:
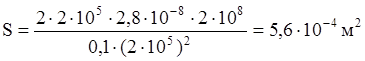
Ответ: 5,6·10-4 м2.
7) Задача на применение закона Био-Савара-Лапласа.
По квадратной рамке со стороной 0,2 м течет ток 4 А. Определить напряженность и индукцию магнитного поля в центре рамки.
Запишем краткое условие задачи.
|
Решение Магнитное поле в центре рамки создается отрезками проводников с током, являющихся сторонами квадрата. |
 Дано:
Дано:
а = 0,2м
 I = 4 A
I = 4 A
B -? H — ?


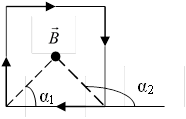 По принципу суперпозиции В = 4В1 где В1 – индукция магнитного поля, создаваемого одной стороной квадрата, по следствию из закона Био-Савара-Лапласа она равна
По принципу суперпозиции В = 4В1 где В1 – индукция магнитного поля, создаваемого одной стороной квадрата, по следствию из закона Био-Савара-Лапласа она равна 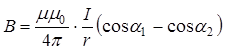 ,
,
здесь r = а/2 – расстояние от проводника до центра квадрата, α1 = 450, α2 = 1350.
Тогда получим расчетную формулу для В:
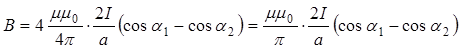
Произведем вычисления:
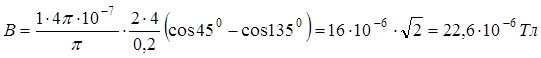
Индукция поля и напряженность связаны соотношением: ![]() .
.
Отсюда 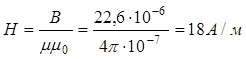
Ответ: 22,6·10-6 Тл; 18 А/м.
8) Задача на применение закона Ампера.
Прямолинейный проводник массой 2 кг и длиной 59 см помещен в однородное магнитное поле перпендикулярно линиям индукции. Какой ток должен проходить по нему, чтобы он висел не падая? Индукция однородного магнитного поля равна 15 Тл.
Запишем краткое условие задачи.
|
Решение: Проводник не будет падать, если сила тяжести |
 Дано: СИ
Дано: СИ
m=2кг
![]() =59см =0,59м
=59см =0,59м
В=15Тл
 α=900
α=900
I-?
Проведем проверку размерности:
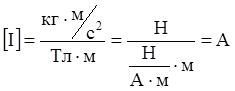 .
.
Произведем вычисления: 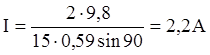 .
.
Ответ: 2,2 А
9) Задача на силу Лоренца.
α-частица, ускоренная разностью потенциалов 250 В, влетает в однородное магнитное поле индукцией 25 мТл, перпендикулярно линиям магнитной индукции и движется по окружности. Найдите радиус окружности и период обращения α-частицы.
Запишем краткое условие задачи.
|
Решение: Работа электрического поля затрачивается на увеличение кинетической энергии частицы: |
 Дано: СИ
Дано: СИ
е=1,6·10-19Кл
mp=1,67·10-27кг
U=250B
B=25мТл =25·10-3Тл
 α=900.
α=900.
R, T-?
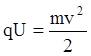
![]()
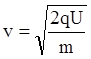 .
.
В магнитном поле на движущуюся заряженную частицу действует сила Лоренца: 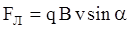 , угол α=900 и
, угол α=900 и 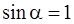 . Согласно второму закону Ньютона
. Согласно второму закону Ньютона 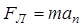 , где
, где 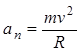 — центростремительное ускорение частицы, движущейся по окружности радиуса R. Получаем
— центростремительное ускорение частицы, движущейся по окружности радиуса R. Получаем 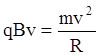 . Окончательно радиус окружности:
. Окончательно радиус окружности: 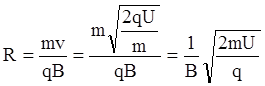 .
.
Период обращения частицы найдем, разделив длину окружности на скорость частицы: 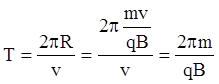 .
.
Заряд α-частицы: 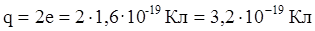 , ее масса
, ее масса ![]()
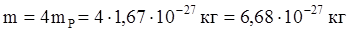
Проведем проверку размерности:
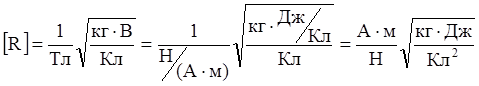 =
=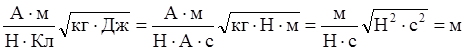
![]()
![]()