Задачи по мсс
ЗАДАЧА № 1.
На тело, погруженное в жидкость, действует только вертикальная (выталкивающая) сила, равная весу вытесненной телом жидкости. При плавании тела сила тяжести равна выталкивающей силе, G = F. Выталкивающая сила равна F = Wρg, или F = Wγ где W — объем вытесняемой телом жидкости, ρ — плотность жидкости; g — ускорение свободного падения, γ — удельный вес воды в Н/м3, гс/см3, кгс/л или тс/м3.
Для гидравлического пресса определить силу D2 при известных N1 = 34 кгс, N2 = 500 кгс, D1 = 2 см
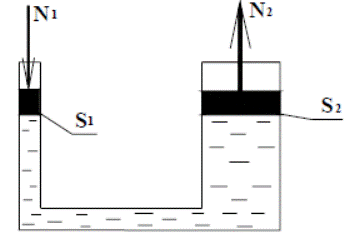
Решение.
Гидростатическое давление под левым поршнем составляет p1=10/1=10
гс/см2 = 10 ат. Это давление передается во всех направлениях одинаково и поэтому под правым поршнем давление будет равно p2 = p1 = 10 кгс/см2.
В то же время N1:πD12/4 = N2:πD22 /4 → N1/D12 = N2/D22
D22 = (N2*D12) / N1
D2 = D1 ![]()
D2 = 7,67 см
ЗАДАЧА № 2.
Насос забирает воду из колодца.
Атмосферное давление Ра = 74 см. рт. столба
Давление во всасывающем патрубке насоса P0 = 0,45 × PА см рт ст
ρрт = 13550 кгс/мм3
γ = 1000 кгс/м3
Определить высоту подъема воды в трубопроводе h.
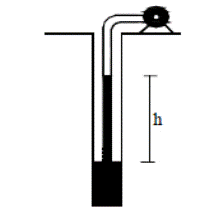
Решение
Pсм. рт. ст = Ра × ρрт = 10027 кгс/мм2
P0 = 0,45 × 10027 = 4512 кгс/м2
Так как мы знаем что, Рa = Рo + γ×h выразим h
h = (Рa – Ро) / γ
h =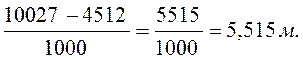
ЗАДАЧА № 3.
Для затвора определить силу давления Р
и расстояние от поверхности воды до центра давления hд
размеры затвора: b = 1 м, h = 1 м,
расстояние от поверхности воды до верхней кромки затвора: Н = 10 м.
площадь затвора: ω = 1 м2
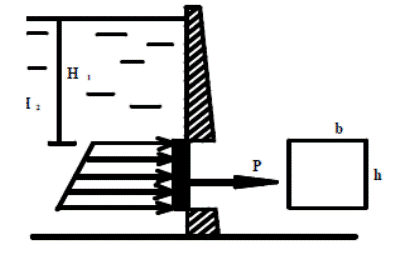
Решение P = γ × hc × ω
hc = H + 1/2 м = 10,5 м
P = 1000 × 10,5 × 1 = 10500 кгс
J (момент инерции прямоугольного затвора) = 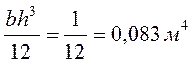
hд = 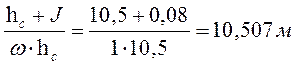
ЗАДАЧА № 4.
В смывном бачке плавает поплавок диаметром D = 13 см
глубина погружения поплавка под уровень воды (осадка) Н = 10 см
длина рычага от шарнира до клапана X = 2 см
Диаметр запирающего поршня d = 0.5 см2 (совпадает с диаметром подводящей трубки)
давление воды в водопроводе P = 2,5 кгс/см2
γ воды 1000 кгс/м3 = 0,001 кгс/см3
Необходимо определить плечо рычага до шарнира L в момент прекращения подачи воды из водопровода (вода из водопровода не будет поступать тогда, когда сила давления рычага на поршень будет больше силы давления на этот же поршень воды).

Решение
L × R1 = R2 × x
R1 = γ × V ![]() R1 = γ ×
R1 = γ × 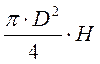
R2 = P × 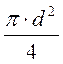
L × γ × 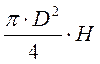 = P ×
= P × 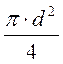 × x
× x
L = 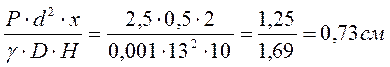
ЗАДАЧА № 5.
Масса груза Мгр = 10 т × с
Массу понтона принять Мп = 1000 кг = 1 т
Допустимая осадка h = 0,3 м
Определить необходимую площадь понтона S
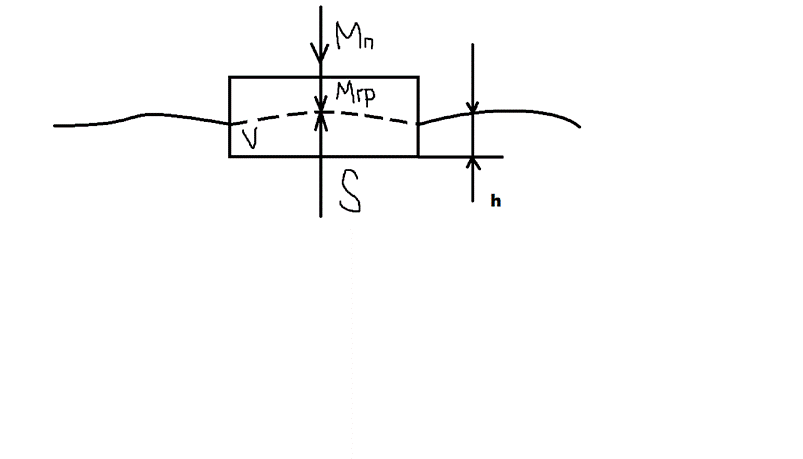
Решение
Мп + Мг = γ × S × h
1 + 10 = γ × S × h
S = 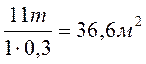
ЗАДАЧА № 6
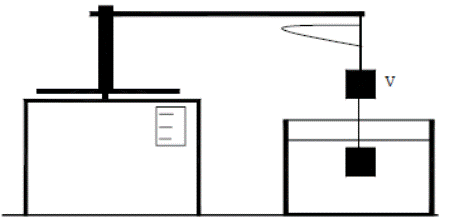
На чашке весов установлен сосуд с водой, над сосудом на кронштейне штатива подвешена гиря объемом V = 0,8 л, показания весов – 5 кгс. Определить показания весов после погружения гири под уровень воды,
объемом V = 0,8 л
Показания весов G = 5 кгс
Гирю погружают под уровень воды (гиря висит на нити, не касаясь дна сосуда). Показания весов после погружения гири G1
Определить G1
Решение
При погружении гири под уровень воды в сосуде на гирю будет действовать выталкивающая сила, равная весу вытесненной телом воды. V = 0,8 л, 0,8 л воды весит 0,8 кгс, поэтому выталкивающая сила будет равна 0,8 кгс, по 3 закону Ньютона на сосуд будет действовать, противоположно направленная сила в 0,8 кгс и поэтому показания весов равны 5,8 кгс.
ЗАДАЧА № 7
В воде плавает стакан диаметром d = 10 см, вес стакана 100 гc, вес груза, который находится в стакане, составляет 400 гc. Определить осадку стакана h.
Решение
Общий вес стакана и груза G = 100+400 = 500 гc.
Площадь стакана определяется по формуле
S = π*d2/4 = 3.14*102/4 =78.5 см2.
G = Fвыт
G = S*h*γ, γводы = 1
G = 500 = 78.5*h*γ
h = 500/( 78.5 * γ)
h = 6,36 см
АДАЧА № 8
В бассейне размерами a*b = 4*5 м
плавает понтон размерами c*d = 2*2 м
На понтоне размещен груз объемом W = 1 м3
вес груза G = 6 тc
ρ = 1025кг/м3
Груз сбрасывается в воду. Определить: 1 – изменится ли уровень воды в бассейне (обосновать); 2 – если уровень воды изменится определить величину изменения уровня.
Решение
Удельный вес груза G/W= 6 тс/м3, следовательно, груз утонет.
∆ Т= G/(ρ*c*d) = 6/(1,025*2*2) = 1,463 м
∆ W = c*d *∆ Т = 4*1,463 = 5,862 м3
После сброса груза объем погруженной части уменьшится на (5,862 — 1)
Разница площадей составляет 16 м2, разница объемов 4,86 м3, разница уровней воды -4,86/16=-0,3 м.
Уровень воды опустится на 30 см.
ЗАДАЧА № 9
Определить расход воды, проходящий через водомер Вентури, если измеренный перепад показаний пьезометров составляет h=0,5 м, диаметры трубопроводов D=0,5 м, d=0,3 м.
Решение
Расход воды найдем по формуле Q = µK h1/2, где µ – коэффициент расхода водомера, учитывающий потери напора в водомере. Для новых водомеров µ = 0,985; для водомеров, бывших в употреблении, µ = 0,98, К — постоянная величина для данного водомера
К = ((π* D2) /4) * (2g/ (D/d)4 – 1))1/2=1,7*0,196=0,33
Q = 0,98*0,33*(0,5)1/2=0,228 м3/с
ЗАДАЧА № 10
Определить диаметр трубопровода и потери напора при расходе воды Q=89 л/с, длине L=0,5 км, температуре t=50 С. Скорость принять 1 м/с. Трубы стальные.
Решение
Скорость V=4Q/π*d2, отсюда d = (4Q/ (π* V))1/2 = 0,336 м
ЗАДАЧА № 11
Вода через отверстие вытекает в атмосферу. Определить диаметр отверстия, напор Н=15 м, скорость V=3 м/с.
Решение
Эта задача не может быть решена, т. к. мы не сможем найти диаметр отверстия из формул расхода воды Q и площади отверстия ω, потому что в исходных данных Q и ω не заданы.
Q=µ *ω*(2g*H)1/2, ω=π*d2/H, Q= V* π*d2/4
ЗАДАЧА № 12
Вода из отверстия распределительной системы выходит со скоростью V=12 м/с. Определить давление воды в трубопроводе.
Решение
V2=2g*H, отсюда Н=2g* V2=2*9,81*144=2822,4


