Закон движения сплошной среды

Получили закон движения сплошной среды. Т. к. вектор перемещений связан с эйлеровыми и лагранжевыми координатами по известным формулам , то из предыдущего получаем

.

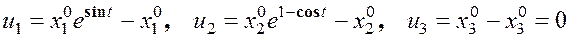Теперь все вспомогательные величины найдены, и мы можем ответить на все вопросы задачи.

1)  Тензор скоростей деформации находим по (4.1) дифференцированием по эйлеровым координатам

.

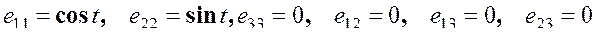2)  Изменение плотности. Воспользуемся уравнением неразрывности, которое запишем в лагранжевых координатах

.

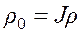Здесь — якобиан перехода от лагранжевых к эйлеровым координатам, который находится по формуле

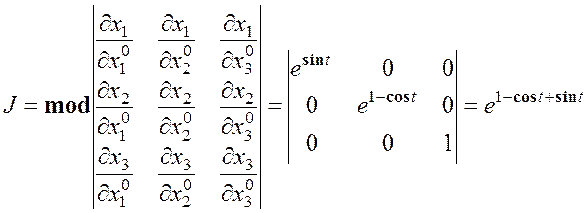
Подставляя это значение в уравнение неразрывности, получаем

.

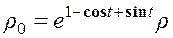Отсюда легко находим

.

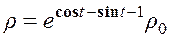Т. е. нашли закон изменения плотности в лагранжевых координатах. Для того, чтобы найти изменение плотности в эйлеровых координатах необходимо закон движения 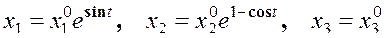подставить в функцию начального распределения плотности

.

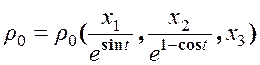Окончательно имеем

.

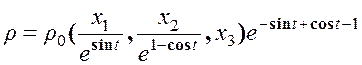3)  Закон движения

.

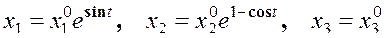4)  Вектор перемещения (как функция лагранжевых координат)

.

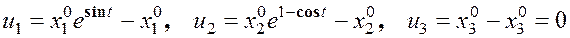5)  Тензор деформаций

.

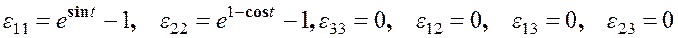Задача полностью решена

Пример 2. Заданы компоненты тензора напряжений в декартовой ортогональной системе координат

.

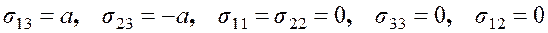Найти главные напряжения, главные оси тензора напряжений и интенсивность напряжений.

Для нахождения главных напряжений воспользуемся известными формулами

.

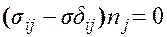Условия существования нетривиального решения по заданному тензору напряжений можно переписать в виде

.

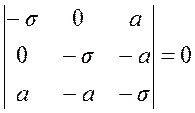Характеристическое уравнение

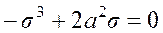
имеет следующие корни

,

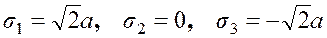которые являются главными напряжениями.

Подставляя первое главное значение в систему уравнений, получим первое главное направление (нормированный вектор)

.

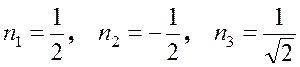Подставляя второе главное значение в систему уравнений, получим второе главное направление (нормированный вектор)

.

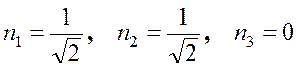И, наконец, также находим третье главное направление

.

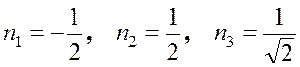Таким образом, главные значения

,

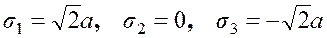главные направления

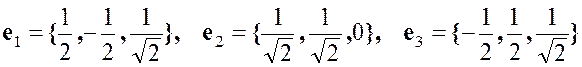
Получили три взаимно ортогональных направления.

Находим интенсивность напряжений. Воспользуемся формулой

,

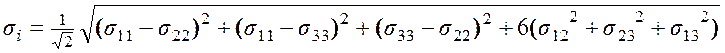в которую подставляем заданные компоненты тензора напряжения

.

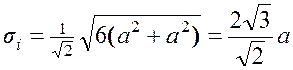Задача полностью решена.

ЗАКЛЮЧЕНИЕ

В настоящем пособии подробно с единых математических позиций представлены положения механики сплошной среды. Рассмотрены основные законы механики и выведены соответствующие уравнения: неразрывности и движения сплошной среды. Кроме введенных тензоров напряжений и деформаций представлены некоторые характеристики, которые необходимы в дальнейшем, при исследовании задач пластичности и разрушения. В пособии используется строгий, но не сложный математический аппарат. Все вводимые физические характеристики снабжены определениями и подробными разъяснениями. Предлагаемые примеры несмотря на свою простоту включают в себя основные положения, разобранные в общей части. Они оказываются полезными для усвоения материала, связанного с пространственным и материальным описанием движения сплошной среды. Настоящее пособие является основной подготовительной частью для дальнейшего описания протекающих процессов в средах с усложненными физическими свойствами.

СПИСОК ЛИТЕРАТУРЫ

1.  Победря Б. Е., Георгиевский Д. В. Основы механики сплошной среды. Курс лекций. М., ФИЗМАТЛИТ, 2006. – 272 с.

2.  Можен М. Механика электромагнитных сплошных сред. М., Мир, 1991. – 560 с.

3.  Ильюшин А. А. Механика сплошной среды. М., Изд. Моск. ун-та, 1990. – 310с.

4.  Седов Л. И. Механика сплошной среды. М., Наука, т. 1, 1976. – 536 с.

5.  Ильюшин А. А., Ломакин В. А., Шмаков А. П. Задачи и упражнения по механике сплошной среды. Изд. Моск. ун-та, 1973. – 164 с.

6.  Галин Г. Я., Голубятников А. Н., Каменярж Я. А., Карликов В. П., Куликовский А. Г., Петров А. Г., Свешникова Е. И., Шикина И. С., Эглит М. Э. Механика сплошных сред в задачах. Том 1: Теория и задачи. М.: «Московский лицей», 1996. — 396 с.

7.  Галин Г. Я., Голубятников А. Н., Каменярж Я. А., Карликов В. П., Куликовский А. Г., Петров А. Г., Свешникова Е. И., Шикина И. С., Эглит М. Э. Механика сплошных сред в задачах. Том 2. Ответы и решения. М.: «Московский лицей», 1996. — 394 с.

8.  Амензаде Ю. А. Теория упругости. М., Высшая школа, 1976. — 272 с.

9.  Снеддон И. Н., Бери Д. С. Классическая теория упругости. М., Гос. изд. физ.-мат. литературы, 1961. — 220 с.

10. Хан Х. Теория упругости. М., Мир, 1988. – 344 с.

11. Голубева О. В. Курс механики сплошных сред. М., высшая школа, 1972. – 368 с.

12. Ионов В. Н., Огибалов П. М. Прочность пространственных элементов конструкций. Ч. 1. Основы механики сплошной среды. М., Высш. шк., 1979. 384 с.