Закон отражения и преломления
Задача 3. Параллельный пучок света шириной 3 см падает под углом 450 из воздуха на плоскую поверхность стекла с показателем преломления 1,5. Какова ширина пучка в стекле?
занятие 1.4.2
закон отражения и преломления. решение
экспериментальных задач
(Повторение геометрической оптики)
1. Определение показателя преломления плоскопараллельной пластинки
 Способ 1. Определение показателя преломления n по действительной и кажущейся толщине пластинки.
Способ 1. Определение показателя преломления n по действительной и кажущейся толщине пластинки.
Оборудование: плоскопараллельная пластинка с вертикальной меткой на одной из граней, пенопластовая “скамейка” с вертикально воткнутой иглой, линейка с делениями.
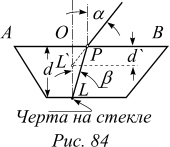 Идея решения. Рассмотрим ход лучей, попадающих в глаз при рассматривании вертикальной черты, нанесенной на заднюю грань пластинки, под малым углом к передней поверхности. На чертеже эта грань горизонтальна. Она видна с ребра AB. Пусть LO и LP выходят из точки L (метки) под малыми углами b. Тогда угол a также мал. Для преломления в точке P выполняется закон Снеллиуса:
Идея решения. Рассмотрим ход лучей, попадающих в глаз при рассматривании вертикальной черты, нанесенной на заднюю грань пластинки, под малым углом к передней поверхности. На чертеже эта грань горизонтальна. Она видна с ребра AB. Пусть LO и LP выходят из точки L (метки) под малыми углами b. Тогда угол a также мал. Для преломления в точке P выполняется закон Снеллиуса: 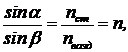 (1)
(1)
но 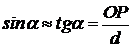 , поэтому
, поэтому 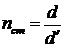 , (2)
, (2)
где d — истинная толщина пластинки, d`— кажущаяся толщина.
Определение кажущейся толщины пластинки d` проводят следующим образом. Рассматривая черту на задней грани через переднюю грань, совмещают иглу с изображением метки. Используя метод параллакса, убеждаются, что произошло совмещение. (Если изменять угол рассматривания, то при отсутствии совмещения при изменении угла изменяется относительное расположение иглы и изображения черты — имеет место относительный параллакс. Если же совмещение произошло, относительный параллакс изображений черты и иглы отсутствует.) Под иглой на матовой поверхности пластинки ставится метка карандашом. После выполнения измерений вычисляется n.
Способ 2
На лист бумаги кладется пластинка. Ее контуры аккуратно обводятся. Под некоторым углом a на бумаге проводится прямая черта LO — “падающий луч”.
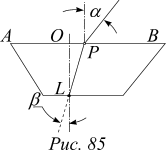 Рассматривая черту через пластинку и изменяя угол зрения надо добиться, чтобы точка L, отмеченная на передней грани пластинки, оказалась на продолжении изображения черты LO, проведенной на бумаге. Потом измеряются углы a и g и по формуле
Рассматривая черту через пластинку и изменяя угол зрения надо добиться, чтобы точка L, отмеченная на передней грани пластинки, оказалась на продолжении изображения черты LO, проведенной на бумаге. Потом измеряются углы a и g и по формуле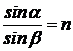
рассчитывается показатель преломления стекла.
Вопрос 1. Какой способ вам кажется точнее? Почему?
2. Определение показателя преломления жидкости
Оборудование: тонкостенный стакан с исследуемой жидкостью, два гвоздика, штатив, линейка.
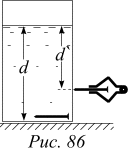 Один из гвоздей укладывается по радиусу на дно стакана (перпендикулярно к боковой стенке). Снаружи на небольшой высоте горизонтально укрепляется второй гвоздь. В сосуд понемногу подливается жидкость до тех пор, пока изображение лежащего на дне гвоздя не приподнимется (вместе с дном) до уровня наружного гвоздя (это положение трудно уловить, будьте внимательны; используйте метод параллакса). По истинной и кажущейся толщине слоя жидкости определите показатель преломления
Один из гвоздей укладывается по радиусу на дно стакана (перпендикулярно к боковой стенке). Снаружи на небольшой высоте горизонтально укрепляется второй гвоздь. В сосуд понемногу подливается жидкость до тех пор, пока изображение лежащего на дне гвоздя не приподнимется (вместе с дном) до уровня наружного гвоздя (это положение трудно уловить, будьте внимательны; используйте метод параллакса). По истинной и кажущейся толщине слоя жидкости определите показатель преломления 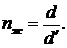
3. Творческое задание
Имея лист бумаги, карандаш, линейку, определите показатель преломления стекла полуцилиндра с матовыми основаниями.
Начертите ход лучей, поясните расчеты.
Подсказка. Попытайтесь использовать явление полного внутреннего отражения.
4. Домашнее задание
Оформите отчеты по решенным экспериментальным задачам в своих тетрадях.
занятие 1.4.3
линзы. решение задач
(Повторение геометрической оптики)
1. Линзы
1.1 Построение изображения в линзе
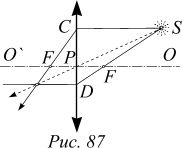 Изображение предмета создается светом, отраженным от предмета, прошедшим оптическую систему и попавшим в глаза наблюдателю. Для построения изображения предмета можно пользоваться любыми из лучей, однако, изо всех лучей есть наиболее удобные для этих целей. У линзы есть несколько особых линий и точек, используемых при построении изображения. Они показаны на рисунке. Во-первых, ось симметрии линзы OO` — главная оптическая ось. Далее: точка P — оптический центр линзы, точки F — фокусы. Фокус линзы замечателен тем, что все лучи, идущие параллельно главной оптической оси, пересекаются в фокусе. Это свойство используется при построении изображения.
Изображение предмета создается светом, отраженным от предмета, прошедшим оптическую систему и попавшим в глаза наблюдателю. Для построения изображения предмета можно пользоваться любыми из лучей, однако, изо всех лучей есть наиболее удобные для этих целей. У линзы есть несколько особых линий и точек, используемых при построении изображения. Они показаны на рисунке. Во-первых, ось симметрии линзы OO` — главная оптическая ось. Далее: точка P — оптический центр линзы, точки F — фокусы. Фокус линзы замечателен тем, что все лучи, идущие параллельно главной оптической оси, пересекаются в фокусе. Это свойство используется при построении изображения.
Пусть S — светящаяся точка, изображение которой следует построить. Из всех лучей, которые идут из точки S и проходят сквозь линзу, выберем луч SC, параллельный главной оптической оси и луч SD, проходящий через фокус. Эти лучи, а, значит, и все остальные отраженные, пересекутся в точке S`. За линзой наблюдатель будет видеть свет, исходящий из точки S`, т. е. точка S` является изображением токи S. Так можно построить изображение любой точки. Все точки любого видимого предмета испускают свет и соответственно дают изображение в линзе — изображение предмета.
В качестве одной из опорных линий можно использовать также луч, который идет из светящейся точки через оптический центр линзы. Этот луч обладает важным свойством — пройдя через линзу, он не изменяет направления. На рисунке 87 он изображен штриховой линией. Как видно, он так же, как и первые два, проходит через изображение.
При построении изображения точки, лежащей на главной оптической оси, используется одна из побочных оптических осей (прямая, проходящая через оптический центр). Все лучи, идущие параллельно побочной оптической оси, пересекаются в точке, лежащей на фокальной плоскости.
1.1.1 Формула линзы
Задача 1. Выведите уравнение, связывающее расстояния от предмета и изображения до оптического центра линзы — a и b – с фокусным расстоянием F:
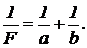 (1)
(1)
Отдельно рассмотрите случаи: a>F; a<F. Что означает результат b<0? (Величина 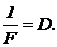 называется оптической силой линзы, измеряется в м-1 или диоптриях.)
называется оптической силой линзы, измеряется в м-1 или диоптриях.)
Формула линзы (1) применима и для вогнутой линзы. Для вогнутой линзы F<0 и b<0.
Технологические особенности изготовления линзы приводят к тому, что ее поверхности оказываются сферами. Если R1 и R2 — радиусы кривизны поверхностей, то оптическая сила линзы задается формулой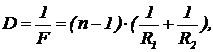 (2)
(2)
где 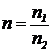 – относительный показатель преломления (n1 – показатель преломления материала линзы, n2 – показатель преломления окружающей среды).
– относительный показатель преломления (n1 – показатель преломления материала линзы, n2 – показатель преломления окружающей среды).
Оптическая сила вплотную сдвинутых тонких линз равна сумме оптических сил:
D=D1+D2+D3+… (3)
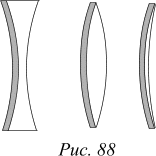 Замечательный частный случай: одна из поверхностей линзы покрыта зеркальным слоем (рисунок 88). Можно считать, что каждая из трех изображенных систем представляет собой вплотную сдвинутые линзу и зеркало. Оптическая сила системы равна сумме оптической силы зеркала и линзы. Особенность данной системы состоит в том, что свет дважды проходит линзу, поэтому приходится считать, что система состоит из вплотную сдвинутых зеркала и двух одинаковых линз. Оптическая сила системы: Dсист=Dзерк+2Dлинз.
Замечательный частный случай: одна из поверхностей линзы покрыта зеркальным слоем (рисунок 88). Можно считать, что каждая из трех изображенных систем представляет собой вплотную сдвинутые линзу и зеркало. Оптическая сила системы равна сумме оптической силы зеркала и линзы. Особенность данной системы состоит в том, что свет дважды проходит линзу, поэтому приходится считать, что система состоит из вплотную сдвинутых зеркала и двух одинаковых линз. Оптическая сила системы: Dсист=Dзерк+2Dлинз.
Задача 2. В вогнутое горизонтально расположенное зеркало с радиусом кривизны R=10 м налили немного воды. На расстоянии 2 м над водой висит лампочка. Где будет ее изображение и каковы его размеры? Показатель преломления воды равен 4/3.
2. Оптические системы
2.1 Оптические системы с разнесенными составляющими
Выясним, как рассчитывается оптическая система линз, отстоящих друг от друга на некотором расстоянии. Один из приемов расчета состоит в последовательном построении изображений. Причем изображение в предыдущей линзе является источником (предметом) для другой. Рассмотрим пример такой задачи.


