Законы динамики
Законы динамики. (Законы Ньютона)
1. Каждое тело пребывает в состоянии покоя или равномерного прямолинейного движения до тех пор, пока действующие на тело силы не заставят его изменить движение (причиной изменения движения является сила).
2. Ускорение пропорционально приложенной силе и направлено вдоль линии действия силы: 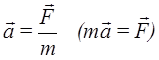 (количественная мера действия силы).
(количественная мера действия силы).
3. Силы взаимодействия двух материальных точек равны по величине и противоположны по направлению ![]() (сила всегда имеет материальный источник, который испытывает обратное действие объекта, к которому приложена сила).
(сила всегда имеет материальный источник, который испытывает обратное действие объекта, к которому приложена сила).
Аксиома о суперпозиции сил
При одновременном действии на материальную точку нескольких сил ускорение точки относительно ИСО от действия каждой отдельной силы не зависит от наличия других приложенных к точке сил и полное ускорение равно векторной сумме ускорений от действия отдельных сил.
Между силами нет взаимного влияния друг на друга в создании ускорения точки:
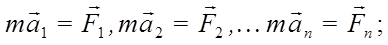
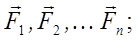
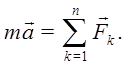
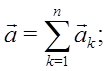
Все это справедливо для небольших скоростей.
Размерностью силы в системе СИ является ньютон ([F]=н). Сила в 1н равна силе, сообщающей телу массой 1 кг ускорение, равное 1 м/с2.
3.3. Дифференциальные уравнения движения материальной точки. Две основные задачи динамики точки
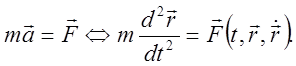
![]() − равнодействующая,
− равнодействующая,
Декартова система координат:
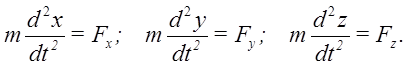
Естественная система координат:
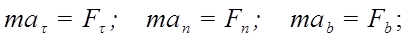
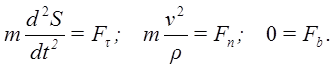
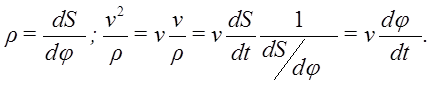 Второе уравнение можно преобразовать:
Второе уравнение можно преобразовать:
Получаем для естественной системы координат:
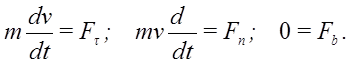
Первая (прямая) задача динамики точки: зная массу точки и ее закон движения, можно найти действующую на точку силу.
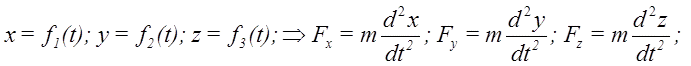
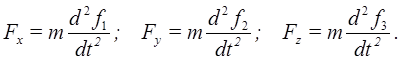
Зная проекции силы на координатные оси, легко определить модуль силы и косинусы углов силы с осями координат.
Пример. Закон движения точки x = aCoskt; y = bSinkt, массы точки m. Определить траекторию и силу, под действием которой происходит движение.
Уравнение траектории:
− эллипс с полуосями a, b
Fx= − mk2aCoskt; Fy= − mk2bSinkt или Fx= − mk2x; Fy= − mk2y;
(r − радиус−вектор точки).
Косинусы углов силы F с осями координат:
Отсюда можно заключить, что сила F имеет направление, противоположное вектору r.
Окончательно .
3.4 Основные виды прямолинейного движения точки.
Криволинейное движение
Дифференциальное уравнение прямолинейного движения точки вдоль оси Ох имеет вид:
если рассматривается случай зависимости силы только от времени, координаты и скорости. Начальные условия задаются в форме:
t=0; x=x0, vx=v0.
Наиболее важные случаи прямолинейного движения точки получаются тогда, когда сила постоянна или она зависит только от времени, координаты х, или от скорости v. Если сила постоянна, то имеем случай равнопеременного движения, то есть движения с постоянным ускорением. Сила зависит от времени обычно, когда ее изменяют путем прямого регулирования. Силу, зависящую от координаты, создает сжатая пружина или центр тяготения. Силы, зависящие от скорости, чаще всего являются силами сопротивления.
Пример 1. Точка массы m движется под действием постоянной силы F с начальной скоростью v0. (t=0, x=0, vx=v0):
используя начальные условия получаем С1=v0
из начальных условий определяем С2=0 и в результате закон движения точки имеет вид:
Пример 2. Точка массы m движется из начального положения покоя под действием переменной силы F = kSinωt. Начальные условия t=0, x=0, vx=0. (рис. 37)

Рис. 37
Из начальных условий определим
(t=0 C2=0)
Получаем, что тело двигается равномерно с постоянной скоростью вправо и на это движение будет накладываться периодическое "модулирующее" движение. Заметим, что составляющей "дрейфа" не было бы, если бы начальные условия имели вид:
Пример 3. Точка массы m брошена вертикально вверх с поверхности земли с начальной скоростью v0 и движется под действием силы тяготения (Рис. 38). Начальные условия: t=0, x=R3, v=v0;
![]()
Имеем дифференциальное уравнение:
Рис. 38
Используя подстановку 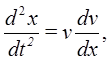 получаем уравнение
получаем уравнение
Разделяем переменные и берем интегралы:
или откуда
(*)
Для определения xmax (максимальная высота подъема), положим v=0, тогда
и при,
это выполняется для v0=11.2 км/с (вторая космическая скорость).
Полученную зависимость (*) скорости точки от высоты подъема можно использовать для определения закона движения (x=f(t)), разделив еще раз переменные и проведя интегрирование.
3.5. Простейшие свойства внутренних сил системы
Механической системой называется любая совокупность материальных точек.
Внешними силами материальной системы называются силы, с которыми действуют на точки системы тела и точки, не входящие в рассматриваемую систему, будем их обозначать .
Внутренними силами материальной системы называют силы взаимодействия между точками рассматриваемой системы(Рис.39), мы их будем обозначать .
Внутренние и внешние силы могут включать в себя как активные силы, так и реакции связей
 Пусть система состоит из n точек. Тогда по третьему закону Ньютона, например, для точек 1 и 2,(рис.39) внутренние силы взаимодействия этих точек равны по величине и противоположны по направлению:
Пусть система состоит из n точек. Тогда по третьему закону Ньютона, например, для точек 1 и 2,(рис.39) внутренние силы взаимодействия этих точек равны по величине и противоположны по направлению: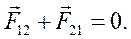
Равнодействующая внутренних сил состоит из векторной суммы сил действия и противодействия, которая
Рис.39 равна нулю: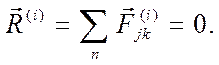
Если рассмотреть сумму моментов сил ![]() и
и ![]() относительно некоторой произвольной точки О, то легко видеть, что
относительно некоторой произвольной точки О, то легко видеть, что

т. к. обе силы имеют одинаковые плечи h и противоположные направления векторных моментов. Главный момент внутренних сил относительно точки О состоит из векторной суммы этих моментов внутренних сил:

3.6. Дифференциальные уравнения движения системы
 Если к каждой точке системы приложить равнодействующую силу внешних сил
Если к каждой точке системы приложить равнодействующую силу внешних сил ![]() и равнодействующую силу всех внутренних сил
и равнодействующую силу всех внутренних сил![]() , то для любой к-ой точки системы можно составить дифференциальное уравнение движения в виде второго закона Ньютона:
, то для любой к-ой точки системы можно составить дифференциальное уравнение движения в виде второго закона Ньютона:


